Combinatorics

Discrete mathematics, graph theory, and enumerative combinatorics

Trending in Combinatorics

2601.00766

Set mappings for general graphs

The study of extremal problems for set mappings has a long history. It was introduced in 1958 by Erdős and Hajnal, who considered the case of cliques in graphs and hypergraphs. Recently, Caro, Patkós, Tuza and Vizer revisited this subject, and initiated the systematic study of set mapping problems for general graphs. In this paper, we prove the following result, which answers one of their questions. Let $G$ be a graph with $m$ edges and no isolated vertices and let $f : E(K_N) \rightarrow E(K_N)$ such that $f(e)$ is disjoint from $e$ for all $e \in E(K_N)$. Then for some absolute constant $C$, as long as $N \geq C m$, there is a copy $G^*$ of $G$ in $K_N$ such that $f(e)$ is disjoint from $V(G^*)$ for all $e \in E(G^*)$. The bound $N = O(m)$ is tight for cliques and is tight up to a logarithmic factor for all $G$.

2601.00766

Jan 2026Combinatorics

Tiling with Boundaries: Dense digital images have large connected components

If most of the pixels in an $n \times m$ digital image are the same color, must the image contain a large connected component? How densely can a given set of connected components pack in $\mathbb{Z}^2$ without touching? We answer these two closely related questions for both 4-connected and 8-connected components. In particular, we use structural arguments to upper bound the "white" pixel density of infinite images whose white (4- or 8-)connected components have size at most $k$. Explicit tilings show that these bounds are tight for at least half of all natural numbers $k$ in the 4-connected case, and for all $k$ in the 8-connected case. We also extend these results to finite images. To obtain the upper bounds, we define the exterior site perimeter of a connected component and then leverage geometric and topological properties of this set to partition images into nontrivial regions called polygonal tiles. Each polygonal tile contains a single white connected component and satisfies a certain maximality property. We then use isoperimetric inequalities to precisely bound the area of these tiles. The solutions to these problems represent new statistics on the connected component distribution of digital images.

2512.11740

Dec 2025Combinatorics

Fault-tolerant mutual-visibility: complexity and solutions for grid-like networks

Networks are often modeled using graphs, and within this setting we introduce the notion of $k$-fault-tolerant mutual visibility. Informally, a set of vertices $X \subseteq V(G)$ in a graph $G$ is a $k$-fault-tolerant mutual-visibility set ($k$-ftmv set) if any two vertices in $X$ are connected by a bundle of $k+1$ shortest paths such that: ($i$) each shortest path contains no other vertex of $X$, and ($ii$) these paths are internally disjoint. The cardinality of a largest $k$-ftmv set is denoted by $\mathrm{f}μ^{k}(G)$. The classical notion of mutual visibility corresponds to the case $k = 0$. This generalized concept is motivated by applications in communication networks, where agents located at vertices must communicate both efficiently (i.e., via shortest paths) and confidentially (i.e., without messages passing through the location of any other agent). The original notion of mutual visibility may fail in unreliable networks, where vertices or links can become unavailable. Several properties of $k$-ftmv sets are established, including a natural relationship between $\mathrm{f}μ^{k}(G)$ and $ω(G)$, as well as a characterization of graphs for which $\mathrm{f}μ^{k}(G)$ is large. It is shown that computing $\mathrm{f}μ^{k}(G)$ is NP-hard for any positive integer $k$, whether $k$ is fixed or not. Exact formulae for $\mathrm{f}μ^{k}(G)$ are derived for several specific graph topologies, including grid-like networks such as cylinders and tori, and for diameter-two networks defined by Hamming graphs and by the direct product of complete graphs.

2512.01978

Dec 2025Combinatorics

2,013 papers

Some recent results in Ramsey theory

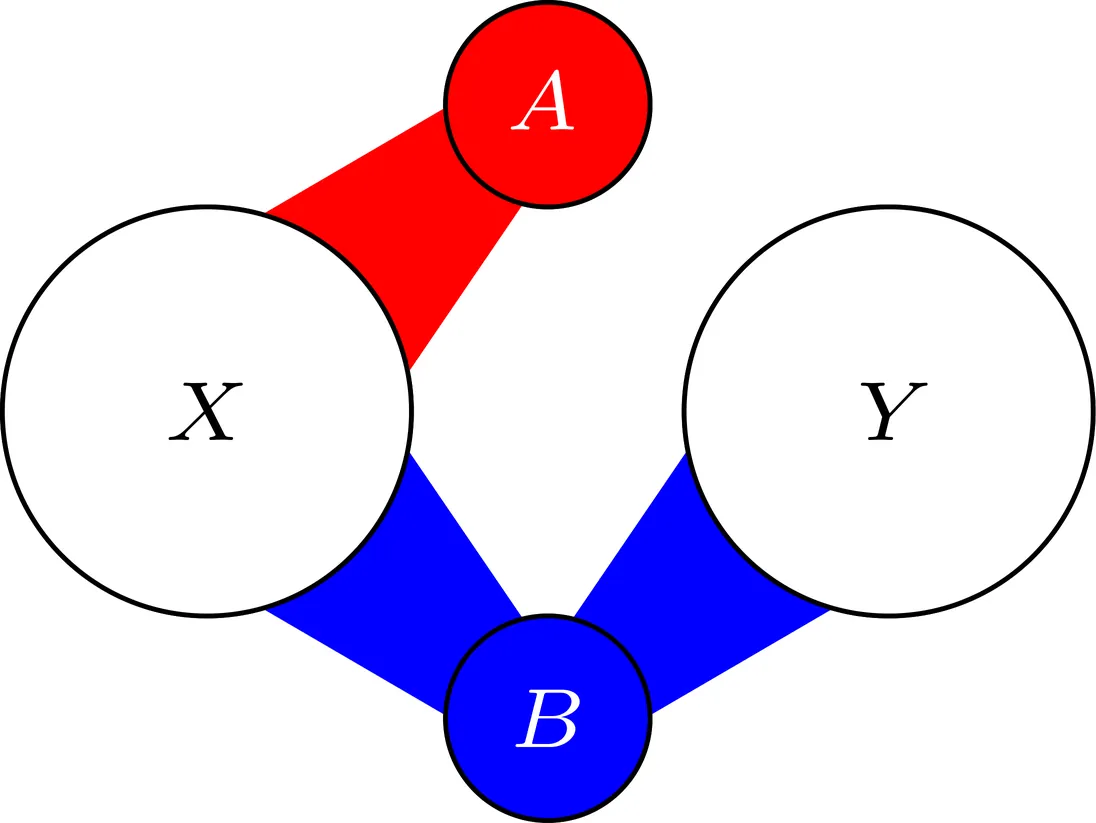
The purpose of this survey is to provide a gentle introduction to several recent breakthroughs in graph Ramsey theory. In particular, we will outline the proofs (due to various groups of authors) of exponential improvements to the diagonal, near-diagonal, and multicolour Ramsey numbers, improved lower bounds on $R(3,k)$ and $R(4,k)$, and an exponential upper bound on the induced Ramsey numbers.

2601.05221Jan 2026

View

Basis Number of Graphs Excluding Minors

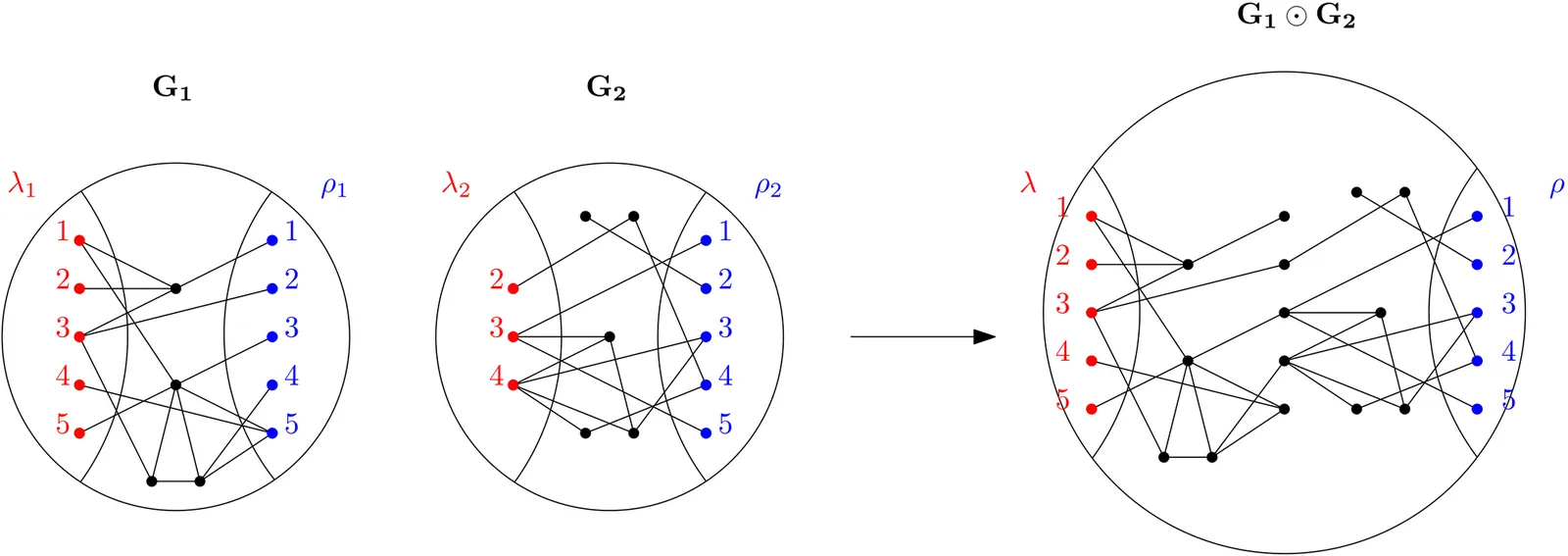
The basis number of a graph $G$ is the minimum $k$ such that the cycle space of $G$ is generated by a family of cycles using each edge at most $k$ times. A classical result of Mac Lane states that planar graphs are exactly graphs with basis number at most 2, and more generally, graphs embedded on a fixed surface are known to have bounded basis number. Generalising this, we prove that graphs excluding a fixed minor $H$ have bounded basis number. Our proof uses the Graph Minor Structure Theorem, which requires us to understand how basis number behaves in tree-decompositions. In particular, we prove that graphs of treewidth $k$ have basis number bounded by some function of $k$. We handle tree-decompositions using the proof framework developed by Bojańczyk and Pilipczuk in their proof of Courcelle's conjecture. Combining our approach with independent results of Miraftab, Morin and Yuditsky (2025) on basis number and path-decompositions, one can moreover improve our upper bound to a polynomial one: there exists an absolute constant $c>0$ such that every $H$-minor free graph has basis number $O(|H|^c)$.

2601.05195Jan 2026

View

Structural properties of nested set complexes

We study structural and topological properties of nested set complexes of matroids with arbitrary building sets, proving that these complexes are vertex decomposable and admit convex ear decompositions. These results unify and generalize several recent and classical theorems on Bergman complexes and augmented Bergman complexes of matroids. As a first application, we show that the $h$-vector of a nested set complex is strongly flawless and, in particular, top-heavy. We then specialize to the boundary complex of the Deligne--Mumford--Knudsen moduli space $\overline{\mathcal{M}}_{0, n}$ of rational stable marked curves, which coincides with the complex of trees, establishing new structural decomposition theorems and deriving combinatorial formulas for its face enumeration polynomials.

2601.05188Jan 2026

View

Neural Algorithmic Reasoning for Approximate $k$-Coloring with Recursive Warm Starts

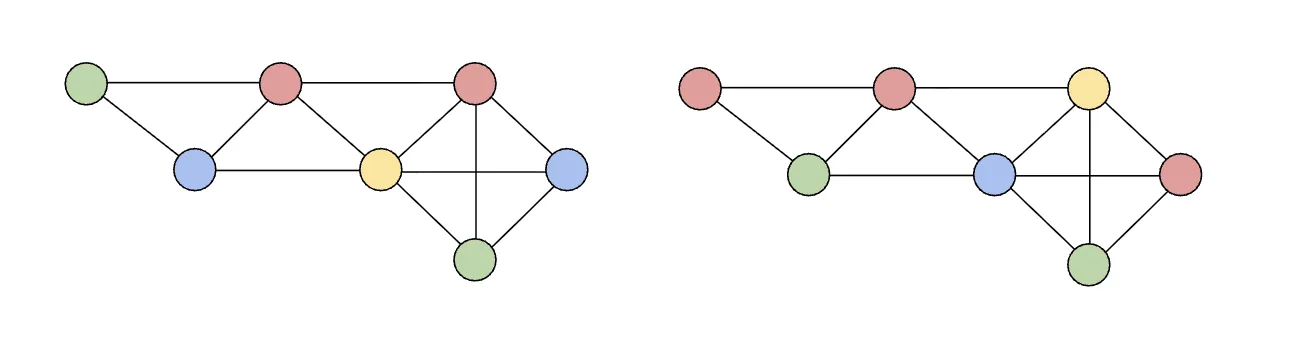
Node coloring is the task of assigning colors to the nodes of a graph such that no two adjacent nodes have the same color, while using as few colors as possible. It is the most widely studied instance of graph coloring and of central importance in graph theory; major results include the Four Color Theorem and work on the Hadwiger-Nelson Problem. As an abstraction of classical combinatorial optimization tasks, such as scheduling and resource allocation, it is also rich in practical applications. Here, we focus on a relaxed version, approximate $k$-coloring, which is the task of assigning at most $k$ colors to the nodes of a graph such that the number of edges whose vertices have the same color is approximately minimized. While classical approaches leverage mathematical programming or SAT solvers, recent studies have explored the use of machine learning. We follow this route and explore the use of graph neural networks (GNNs) for node coloring. We first present an optimized differentiable algorithm that improves a prior approach by Schuetz et al. with orthogonal node feature initialization and a loss function that penalizes conflicting edges more heavily when their endpoints have higher degree; the latter inspired by the classical result that a graph is $k$-colorable if and only if its $k$-core is $k$-colorable. Next, we introduce a lightweight greedy local search algorithm and show that it may be improved by recursively computing a $(k-1)$-coloring to use as a warm start. We then show that applying such recursive warm starts to the GNN approach leads to further improvements. Numerical experiments on a range of different graph structures show that while the local search algorithms perform best on small inputs, the GNN exhibits superior performance at scale. The recursive warm start may be of independent interest beyond graph coloring for local search methods for combinatorial optimization.

2601.05137Jan 2026

View

2601.05119

Line Shellings of Geometric Lattices

Inspired by Bruggesser-Mani's line shellings of polytopes, we introduce line shellings for the lattice of flats of a matroid: given a normal complex for a Bergman fan of a matroid induced by a building set, we show that the lexicographic order of the coordinates of its vertices is a shelling order. This gives a new proof of Björner's classical result that the order complex of the lattice of flats of a matroid is shellable, and demonstrates shellability for all nested set complexes for matroids.

2601.05119Jan 2026

View

L-log-concavity and a proof of the conjecture of Lam, Postnikov and Pylyavskyy

Let $λ$, $μ$, $λ'$, $μ'$ be partitions. The conjecture of Lam, Postnikov and Pylyavskyy states that, if $λ+μ= λ' + μ'$, and $\min(λ_i-λ_j, μ_i-μ_j) \leq λ'_i - λ'_j \leq \max(λ_i-λ_j, μ_i-μ_j)$ for all $1 \leq i<j \leq n$, then $s_{λ'} s_{μ'} - s_λ s_μ$ is Schur nonnegative. We prove this conjecture. Our proof is based on two key ideas. First, we introduce a new combinatorial model for Littlewood-Richardson coefficients which we name ``skeps", which are similar to but distinct from Knutson and Tao's hives. Second, we use tools from Murota's theory of L-convexity to prove an L-log-concavity theorem for skeps.

2601.05007Jan 2026

View

Stability results for Berge-matching in hypergraphs

Given a graph $F$, a hypergraph is called a Berge-$F$ if it can be obtained by expanding each edge of $F$ into a hyperedge containing it. Let $M_{k}$ denote the matching of size $k$. Kang, Ni, and Shan [12] determined the Turán number of Berge-$M_k$. Our main result shows that if an $r$-uniform hypergraph $H$ on $n$ vertices has nearly as many edges as the extremal in their theorem without containing $M_k$, then $H$ must be structurally close to certain well-specified graphs. Meanwhile, our result also implies several stability results, such as the stability version of the well-known Erdős-Gallai theorem (Erdős and Gallai, 1959 [5]).

2601.04929Jan 2026

View

Arboreal Ultrametrics

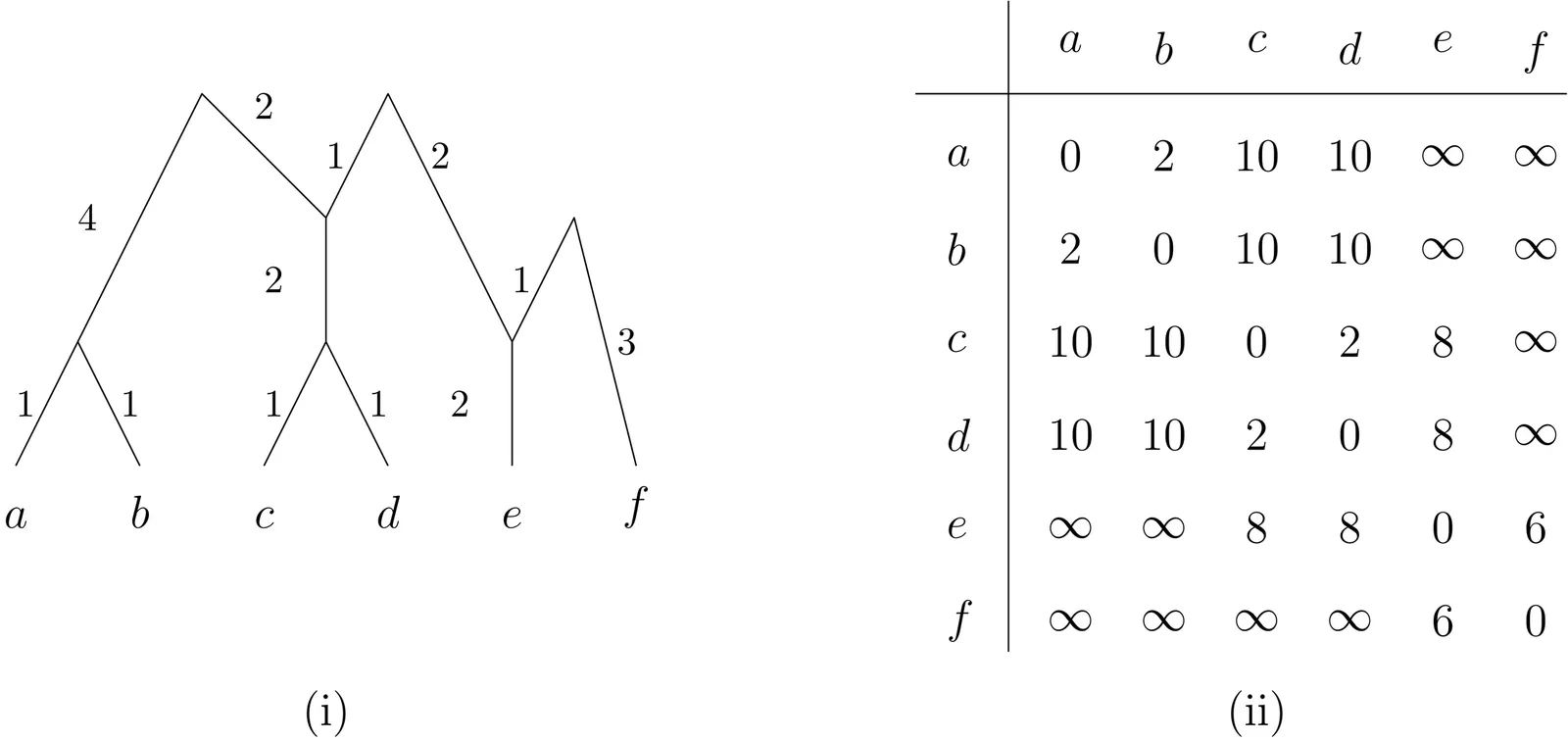
Ultametrics are an important class of distances used in applications such as phylogenetics, clustering and classification theory. Ultrametrics are essentially distances that can be represented by an edge-weighted rooted tree so that all of the distances in the tree from the root to any leaf of the tree are equal. In this paper, we introduce a generalization of ultrametrics called arboreal ultrametrics which have applications in phylogenetics and also arise in the theory of distance-hereditary graphs. These are partial distances, that is distances that are not necessarily defined for every pair of elements in the groundset, that can be represented by an ultrametric arboreal network, that is, an edge-weighted rooted network whose underlying graph is a tree. As with ultrametrics all of the distances in the ultrametric arboreal network from any root to any leaf below it are are equal but, in contrast, the network may have more than one root. In our two main results we characterize when a partial distance is an arboreal ultrametric as well as proving that, somewhat surprisingly, given any unrooted edge-weighted phylogenetic tree there is a necessarily unique way to insert roots into this tree so as to obtain an arboreal ultrametric.

2601.04836Jan 2026

View

Asymptotic enumeration of constrained bipartite, directed and oriented graphs by degree sequence

In the sufficiently sparse case, we find the probability that a uniformly random bipartite graph with given degree sequence contains no edge from a specified set of edges. This enables us to enumerate loop-free digraphs and oriented graphs with given in-degree and out-degree sequences, and obtain subgraph probabilities. Our theorems are not restricted to the near-regular case. As an application, we determine the expected permanent of sparse or very dense random matrices with given row and column sums; in the regular case, our formula holds over all densities. We also draw conclusions about the degrees of a random orientation of a random undirected graph with given degrees, including its number of Eulerian orientations.

2601.04822Jan 2026

View

More on spectral supersaturation for the bowtie

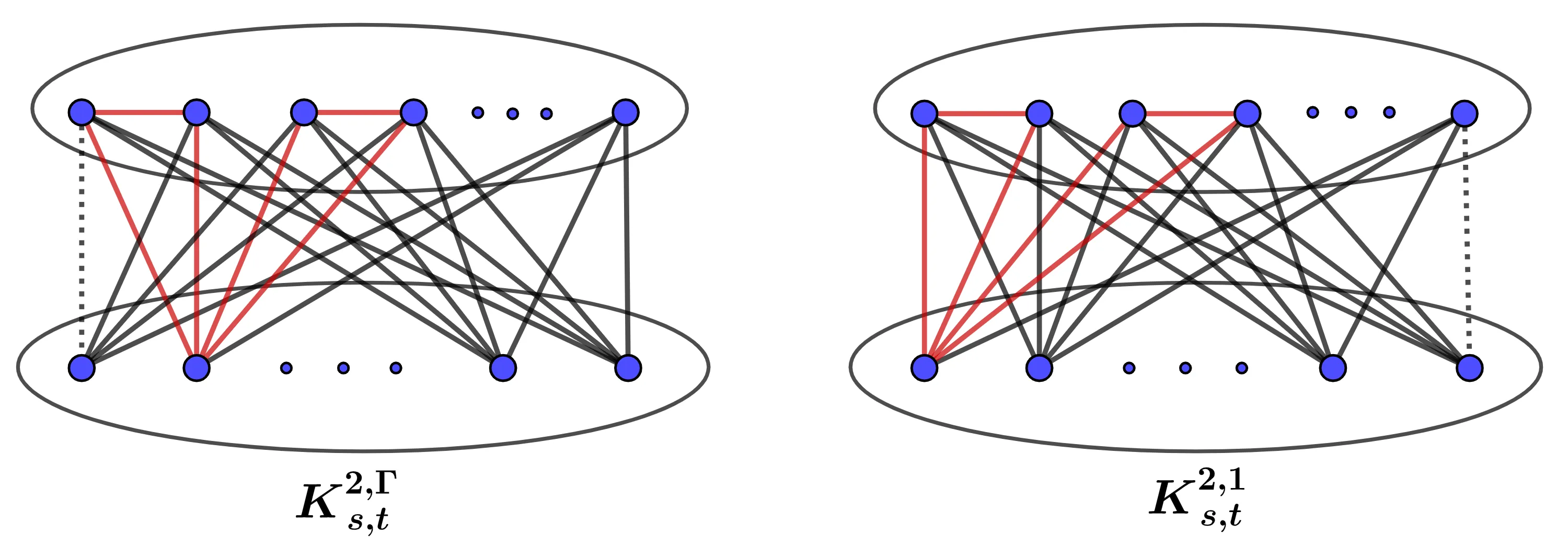
A central topic in extremal graph theory is the supersaturation problem, which studies the minimum number of copies of a fixed substructure that must appear in any graph with more edges than the corresponding Turán number. Significant works due to Erdős, Rademacher, Lovász and Simonovits investigated the supersaturation problem for the triangle. Moreover, Kang, Makai and Pikhurko studied the case for the bowtie, which consists of two triangles sharing a vertex. Building upon the pivotal results established by Bollobás, Nikiforov, Ning and Zhai on counting triangles via the spectral radius, we study in this paper the spectral supersaturation problem for the bowtie. Let $λ(G)$ be the spectral radius of a graph $G$, and let $K_{\lceil \frac{n}{2}\rceil, \lfloor \frac{n}{2}\rfloor}^q$ be the graph obtained from Turán graph $T_{n,2}$ by adding $q$ pairwise disjoint edges to the partite set of size $\lceil \frac{n}{2}\rceil$. Firstly, we prove that there exists an absolute constant $δ>0$ such that if $n$ is sufficiently large, $2\le q \le δ\sqrt{n}$, and $G$ is an $n$-vertex graph with $λ(G)\ge λ(K_{\lceil \frac{n}{2}\rceil, \lfloor \frac{n}{2}\rfloor}^q)$, then $G$ contains at least ${q\choose 2}\lfloor \frac{n}{2}\rfloor$ bowties, and $K_{\lceil \frac{n}{2}\rceil, \lfloor \frac{n}{2}\rfloor}^q$ is the unique spectral extremal graph. This solves an open problem proposed by Li, Feng and Peng. Secondly, we show that a graph $G$ whose spectral radius exceeds that of the spectral extremal graph for the bowtie must contain at least $\lfloor \frac{n-1}{2}\rfloor$ bowties. This sharp bound reveals a distinct phenomenon from the edge-supersaturation case, which guarantees at least $\lfloor \frac{n}{2}\rfloor$ bowties.

2601.04671Jan 2026

View

2601.04637

Large induced forests in planar multigraphs

For a graph $G$ on $n$ vertices, denote by $a(G)$ the number of vertices in the largest induced forest in $G$. The Albertson-Berman conjecture, which is open since 1979, states that $a(G) \geq \frac{n}{2}$ for all simple planar graphs $G$. We show that the version of this problem for multigraphs (allowing parallel edges) is easily reduced to the problem about the independence number of simple planar graphs. Specifically, we prove that $a(M) \geq \frac{n}{4}$ for all planar multigraphs $M$ and that this lower bound is tight. Then, we study the case when the number of pairs of vertices with parallel edges, which we denote by $k$, is small. In particular, we prove the lower bound $a(M) \geq \frac{2}{5}n-\frac{k}{10}$ and that the Albertson-Berman conjecture for simple planar graphs, assuming that it holds, would imply the lower bound $a(M) \geq \frac{n-k}{2}$ for planar multigraphs, which would be better than the general lower bound when $k$ is small. Finally, we study the variant of the problem where the plane multigraphs are prohibited from having $2$-faces, which is the main non-trivial problem that we introduce in this article. For that variant without $2$-faces, we prove the lower bound $a(M) \geq \frac{3}{10}n+\frac{7}{30}$ and give a construction of an infinite sequence of multigraphs with $a(M)=\frac{3}{7}n+\frac{4}{7}$.

2601.04637Jan 2026

View

On identity Seidel switches

Seidel switching is a classical operation on graphs which plays a central role in the theory of two-graphs, signed graphs, and switching classes. In this paper we focus on those switches which leave a given graph invariant up to isomorphism. We call such subsets of the vertex set \emph{identity Seidel switches}. After recalling basic properties of Seidel switching and the associated abelian group structure, we introduce Seidel equivalence classes of graphs and then study the structure of the family of identity Seidel switches of a fixed graph. We show that this family forms a 14 pages; 2--group under composition, and we obtain structural constraints on graphs in which many vertices or edges give rise to identity switches. In particular, we derive necessary conditions in terms of degree parameters, and we characterize certain edge-identity switches via an automorphism of an induced subgraph. Several constructions and examples are presented, and some open problems are proposed.

2601.04530Jan 2026

View

2601.04514

Two conjectures in spectral hypergraph theory

Let $\mathcal{A}$ be a $k$-th order $n$-dimensional tensor, and we denote by ${\rm am}(λ, \mathcal{A})$ the algebraic multiplicity of the eigenvalue $λ$ of $\mathcal{A}$. The projective eigenvariety $\mathbb{V}_λ(\mathcal{A})$ is defined as the set of eigenvectors of $\mathcal{A}$ associated with $λ$, considered in the complex projective space. For a connected uniform hypergraph $H$, let $\mathcal{A}(H)$ and $\mathcal{L}(H)$ denote its adjacency tensor and Laplacian tensor, respectively. Let $ρ$ be the spectral radius of $\mathcal{A}(H)$, for which it is known that $|\mathbb{V}_ρ(\mathcal{A}(H))| = |\mathbb{V}_{0}(\mathcal{L}(H))|$. Recently, Fan [arXiv:2410.20830v2, 2024] conjectured that ${\rm am}(ρ, \mathcal{A}(H)) = |\mathbb{V}_ρ(\mathcal{A}(H))|$ and ${\rm am}(0, \mathcal{L}(H)) = {\rm am}(ρ, \mathcal{A}(H))$. In this paper, we prove these two conjectures, and thereby establish $$ {\rm am}(ρ, \mathcal{A}(H)) = |\mathbb{V}_ρ(\mathcal{A}(H))| = |\mathbb{V}_{0}(\mathcal{L}(H))| = {\rm am}(0, \mathcal{L}(H)). $$ As shown by Fan et al., $|\mathbb{V}_ρ(\mathcal{A}(H))|$ and $|\mathbb{V}_{0}(\mathcal{L}(H))|$ can be computed via the Smith normal form of the incidence matrix of $H$ over $\mathbb{Z}_{k}$. Consequently, we provide a method for computing the algebraic multiplicity of the spectral radius and zero Laplacian eigenvalue for connected uniform hypergraphs.

2601.04514Jan 2026

View

2601.04454

Proof of Convergence of a Laplace Expansion Algorithm For Calculating Recursions Satisfied by a Family of Determinants

In Evan and Hendel's recent proof of an outstanding conjecture on the resistance distances of a family of linear 3-trees, a key technique in the proof was calculating the recursion satisfied by a family of determinants. The underlying algorithm employed to prove the conjecture converged (i.e. terminated) in the particular case studied, and the paper presented an open question on when such a procedure converges in general. This paper proves convergence of the procedure for an arbitrary family of determinants of banded, square, Toeplitz matrices. Moreover, the algorithm in this paper improves several aspects of the algorithm of Evans and Hendel.

2601.04454Jan 2026

View

2601.04409

Positive expansions of permuted basement and quasisymmetric Macdonald polynomials at $t=0$

It is well known that the $q$-Whittaker polynomials, which are $t=0$ specializations of the Macdonald polynomials $P_λ(X;q,t)$, expand positively as the sum of Schur polynomials. Macdonald polynomials have a quasisymmetric refinement: the quasisymmetric Macdonald polynomials $G_γ(X;q,t)$, and a nonsymmetric refinement: the ASEP polynomials $f_α(X;q,t)$. We study the $t=0$ specializations of both these families of polynomials and show analogous properties: the quasisymmetric Macdonald polynomials expand positively as a sum of quasisymmetric Schur functions, $\text{QS}_γ(X)$, and the ASEP polynomials expand positively as a sum of Demazure atoms, $\mathcal{A}_α(X)$. As a corollary of the latter, we prove more generally that any permuted basement Macdonald polynomial has a positive expansion in the Demazure atoms at $t=0$. We give a description of the structure coefficients of $G_γ(X;q,0)$ and $f_α(X;q,0)$ in both cases in terms of the charge statistic on a restricted set of semistandard tableaux.

2601.04409Jan 2026

View

Metric general position extensions of classical graph invariants

We introduce a two-parameter framework that refines several classical graph invariants by imposing higher-order constraints along bounded-length geodesics. For integers $k,d\ge1$, a vertex set is called $k,d$-independent if every shortest path of length at most $d$ contains fewer than $k$ vertices of the set, giving rise to corresponding $k,d$-independence, chromatic, clique, and domination invariants. We develop a general framework for these parameters by associating each graph with a $k$-uniform hypergraph that encodes its geodesic structure. We then establish basic bounds and monotonicity properties, and introduce a notion of $k,d$-perfection extending the classical theory of perfect graphs. Exact formulas are obtained for the $k,d$-chromatic number of paths and cycles. In particular, all paths are $k,d$-perfect for all parameters, while cycles admit a complete classification of $k,d$-perfection that recovers the classical case when $k=2$ and exhibits new periodic and finite-exception behavior for $k\ge3$. We further investigate the interaction between $k,d$-invariants and graph powers, showing that while the $k=2$ case reduces to graph powers in a straightforward way, substantially different behavior arises for higher values of $k$, even for powers of paths.

2601.04351Jan 2026

View

2601.04182

Saturation property fails for Schubert coefficients

The saturation property for Littlewood--Richardson coefficients was established by Knutson and Tao in 1999. In 2004, Kirillov conjectured that the saturation property extends to Schubert coefficients. We disprove this conjecture in a strong form, by showing that it fails for a large family of instances. We also refute the saturation property for Schubert coefficients under bit scaling and discuss computational complexity implications.

2601.041821Jan 2026

View

2601.04125

Recovering of the Grassmann graph from the subgraph of non-degenerate subspaces

Let ${\mathbb F}$ be a (not necessarily finite) field. A subspace of the vector space ${\mathbb F}^n$ is called {\it non-degenerate} if it is not contained in a coordinate hyperplane. We show that the Grassmann graph of $k$-dimensional subspaces of ${\mathbb F}^n$, $1<k<n-1$, can be recovered from the subgraph of non-degenerate subspaces if $|{\mathbb F}|>n-k$. In the case when ${\mathbb F}={\mathbb F}_q$ is the field of $q$ elements, this subgraph is known as the graph of non-degenerate linear $[n,k]_q$ codes.

2601.04125Jan 2026

View

2601.04084

Exact Bounds for Forbidden Configurations and the Extremal Matrices

Let $F$ be a $k\times \ell$ (0,1)-matrix. A matrix is simple if it is a (0,1)-matrix with no repeated columns. A (0,1)-matrix $A$ is said to have a $F$ as a configuration if there is a submatrix of $A$ which is a row and column permutation of $F$. In the language of sets, a configuration is a trace. Let $\mathrm{Avoid}(m,F)$ be all simple $m$-rowed matrices $A$ with no configuration $F$. Define $\mathrm{forb}(m,F)$ as the maximum number of columns of any matrix in $\mathrm{Avoid}(m,F)$. The $2\times (p+1)$ (0,1)-matrix $F(0,p,1,0)$ consists of a row of $p$ 1's and a row of one 1 in the remaining column. The paper determines $\mathrm{forb}(m,F(0,p,1,0))$ for $1\le p\le 9$ and the extremal matrices are characterized. A construction may be extremal for all $p$.

2601.04084Jan 2026

View

Patterns in sequences

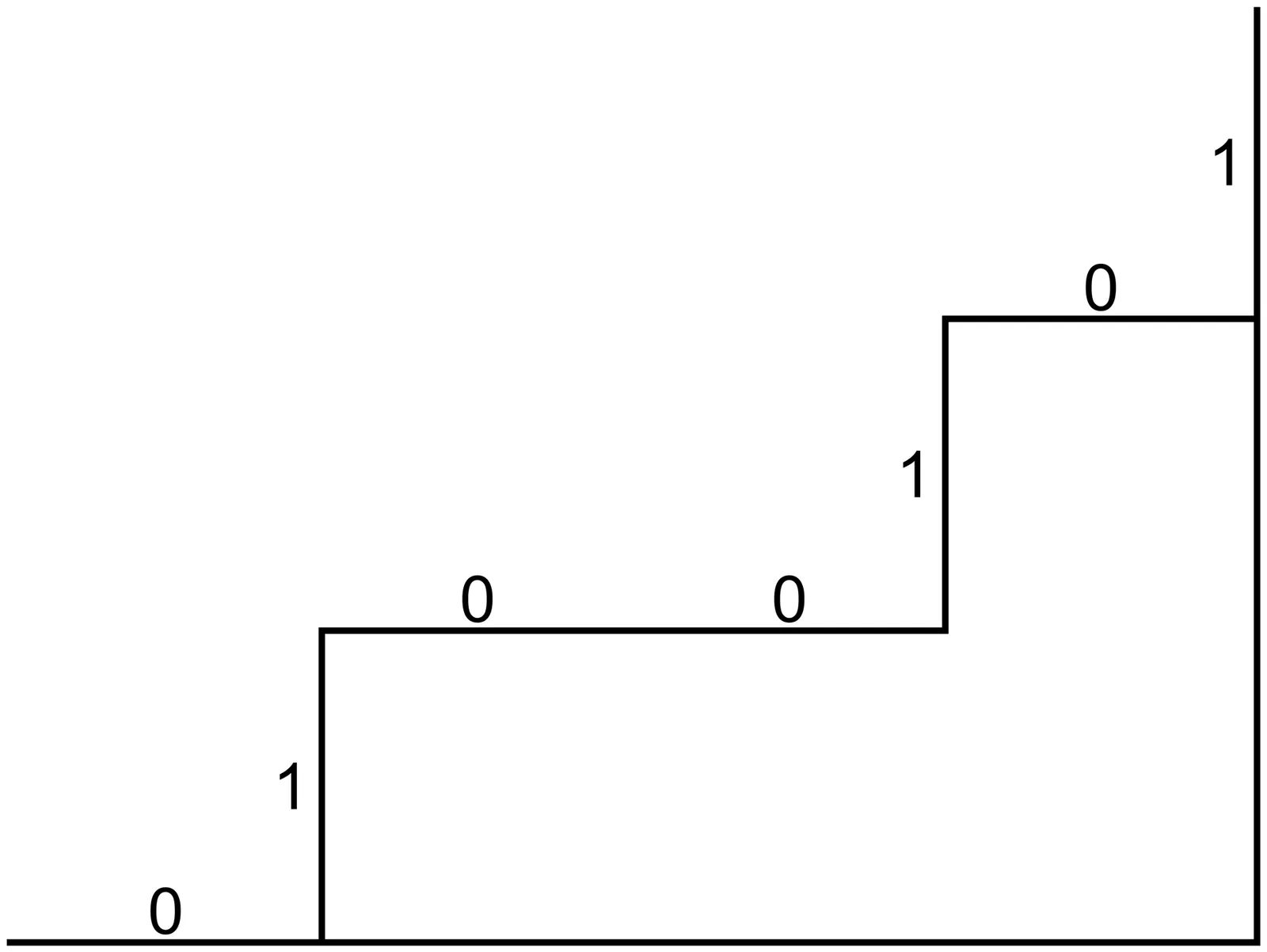
We study pattern densities in binary sequences, finding optimal limit sequences with fixed pattern densities.

2601.04078Jan 2026

View

Page 1 of 101