Discrete Mathematics
Covers combinatorics, graph theory, applications of probability. Roughly includes material in ACM Subject Classes G.2 and G.3.
Covers combinatorics, graph theory, applications of probability. Roughly includes material in ACM Subject Classes G.2 and G.3.
 2512.24850
2512.24850Erdős and Lov'asz asked whether there exists a "3-critical" 3-uniform hypergraph in which every vertex has degree at least 7. The original formulation does not specify what 3-critical means, and two non-equivalent notions have appeared in the literature and in later discussions of the problem. In this paper we resolve the question under both interpretations. For the transversal interpretation (criticality with respect to the transversal number), we prove that a 3-uniform hypergraph $H$ with $τ(H)=3$ and $τ(H-e)=2$ for every edge $e$ has at most 10 edges; in particular, $δ(H)\le 6$, and this bound is sharp, witnessed by the complete 3-graph $K^{(3)}_5$. For the chromatic interpretation (criticality with respect to weak vertex-colourings), we give an explicit 3-uniform hypergraph on 9 vertices with $χ(H)=3$ and minimum degree $δ(H)=7$ such that deleting any single edge or any single vertex makes it 2-colourable. The criticality of the example is certified by explicit witness 2-colourings listed in the appendices, together with a short verification script.
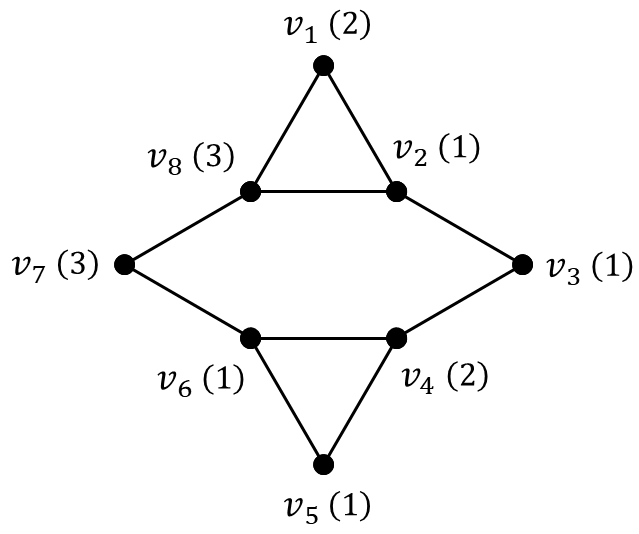
A Roman dominating function for a (non-weighted) graph $G=(V,E)$, is a function $f:V\rightarrow \{0,1,2\}$ such that every vertex $u\in V$ with $f(u)=0$ has at least {one} neighbor $v\in V$ such that $f(v)=2$. The minimum weight $\sum_{v\in V}f(v)$ of a Roman {dominating function} $f$ on $G$ is called the Roman domination number of $G$ and is denoted by $γ_{R}(G)$. A graph {$G= (V,E)$} together with a positive real-valued weight-function $w:V\rightarrow \mathbf{R}^{>0}$ is called a {\it weighted graph} and is denoted by $(G;w)$. The minimum weight $\sum_{v\in V}f(v)w(v)$ of a Roman {dominating function} $f$ on $G$ is called the weighted Roman domination number of $G$ and is denoted by $γ_{wR}(G)$. The domination and Roman domination numbers of unweighted graphs have been extensively studied, particularly for their applications in bioinformatics and computational biology. However, graphs used to model biomolecular structures often require weights to be biologically meaningful. In this paper, we initiate the study of the weighted Roman domination number in weighted graphs. We first establish several bounds for this parameter and present various realizability results. Furthermore, we determine the exact values for several well-known graph families and demonstrate an equivalence between the weighted Roman domination number and the differential of a weighted graph.
For some geometric graph classes, tractability of testing first-order formulas is precisely characterised by the graph parameter twin-width. This was first proved for interval graphs among others in [BCKKLT, IPEC '22], where the equivalence is called delineation, and more generally holds for circle graphs, rooted directed path graphs, and $H$-graphs when $H$ is a forest. Delineation is based on the key idea that geometric graphs often admit natural vertex orderings, allowing to use the very rich theory of twin-width for ordered graphs. Answering two questions raised in their work, we prove that delineation holds for intersection graphs of non-degenerate axis-parallel unit segment graphs, but fails for visibility graphs of 1.5D terrains. We also prove delineation for intersection graphs of circular arcs.
 2512.13999
2512.13999Vizing's theorem states that every simple undirected graph can be edge-colored using fewer than $Δ+ 1$ colors, where $Δ$ is the graph's maximum degree. The original proof was given through a polynomial-time algorithmic procedure that iteratively extends a partial coloring until it becomes complete. In this work, I used the Lean theorem prover to produce a verified implementation of the Misra and Gries edge-coloring algorithm, a modified version of Vizing's original method. The focus is on building libraries for relevant mathematical objects and rigorously maintaining required invariants.

We show how the software Walnut can be used to obtain concise proofs of results concerning variants of the famous Wythoff game, in which blocking maneuvers or terminal positions are added, as discussed respectively by Larsson (2011) and Komak et al. (2025). Our approach provides automatic proofs that both confirm and extend their results, and the same techniques apply to newly introduced variants as well. Then, using classic techniques, we obtain new recursive and morphic characterizations of Wythoff-type games where the set of terminal positions $(x,y)$ satisfy $x+y\le\ell$. The use of Walnut in combinatorial game theory is relatively recent, and only a few examples have been explored so far. The Wythoff game, being directly connected to the Fibonacci numeration system, proves especially well-suited to this kind of approach. It permits us to solve instances for a fixed value of a parameter.
In this article, we give two extended space formulations, respectively, for the induced tree and path polytopes of chordal graphs with vertex and edge variables. These formulations are obtained by proving that the induced tree and path extended incidence vectors of chordal graphs form Hilbert basis. This also shows that both polytopes have the integer decomposition property in chordal graphs. Whereas the formulation for the induced tree polytope is easily seen to have a compact size, the system we provide for the induced path polytope has an exponential number of inequalities. We show which of these inequalities define facets and exhibit a superset of the facet-defining ones that can be enumerated in polynomial time. We show that for some graphs, the latter superset contains redundant inequalities. As corollaries, we obtain that the problems of finding an induced tree or path maximizing a linear function over the edges and vertices are solvable in polynomial time for the class of chordal graphs.
Given an input graph and weights on its vertices, the maximum co-2-plex problem is to find a subset of vertices maximizing the sum of their weights and inducing a graph of degree at most 1. In this article, we analyze polyhedral aspects of the maximum co-2-plex problem. The co-2-plexes of a graph are known to be in bijection with the stable sets of an auxiliary graph called the utter graph~\cite{dupontbouillard2024contractions}. We use this bijection to characterize contraction perfect graphs' co-2-plex polytopes in an extended space. It turns out that the total dual integrality of the associated linear system also characterizes contraction perfectness of the input graph. By projecting this extended space formulation, we obtain the natural variable space description of the co-2-plex polytopes of trees. This projection yields a new family of valid inequalities for the co-2-plex polytope and we characterize when they define facets. Moreover, we show that these inequalities can be separated in polynomial time. We characterize the graphs for which this formulation describes an integer polytope. These linear systems are extended to valid integer linear programs (ILPs) for the maximum co-2-plex problem whose linear relaxation values are tighter than the state of the art for this problem~\cite{bala}. Finally, we provide an experimental comparison of several implementations of our new ILP formulations with the state-of-the-art ILP for this problem and analyze their respective performances relatively to the density of the input graphs.
The mim-width of a graph is a powerful structural parameter that, when bounded by a constant, allows several hard problems to be polynomial-time solvable - with a recent meta-theorem encompassing a large class of problems [SODA2023]. Since its introduction, several variants such as sim-width and omim-width were developed, along with a linear version of these parameters. It was recently shown that mim-width and all these variants all paraNP-hard, a consequence of the NP-hardness of distinguishing between graphs of linear mim-width at most 1211 and graphs of sim-width at least 1216 [ICALP2025]. The complexity of recognizing graphs of small width, particularly those close to $1$, remained open, despite their especially attractive algorithmic applications. In this work, we show that the width recognition problems remain NP-hard even on small widths. Specifically, after introducing the novel parameter Omim-width sandwiched between omim-width and mim-width, we show that: (1) deciding whether a graph has sim-width = 1, omim-width = 1, or Omin-width = 1 is NP-hard, and the same is true for their linear variants; (2) the problems of deciding whether mim-width $\leq$ 2 or linear mim-width $\leq$ 2 are both NP-hard. Interestingly, our reductions are relatively simple and are from the Unrooted Quartet Consistency problem, which is of great interest in computational biology but is not commonly used (if ever) in the theory of algorithms.
In this work we take a step towards characterising strongly flip-flat classes of graphs. Strong flip-flatness appears to be the analogue of uniform almost-wideness in the setting of dense classes of graphs. We prove that strongly flip-flat classes of graphs that are weakly sparse are indeed uniformly almost-wide.
We prove that the lonely runner conjecture holds for nine runners. Our proof is based on a couple of improvements of the method we used to prove the conjecture for eight runners.
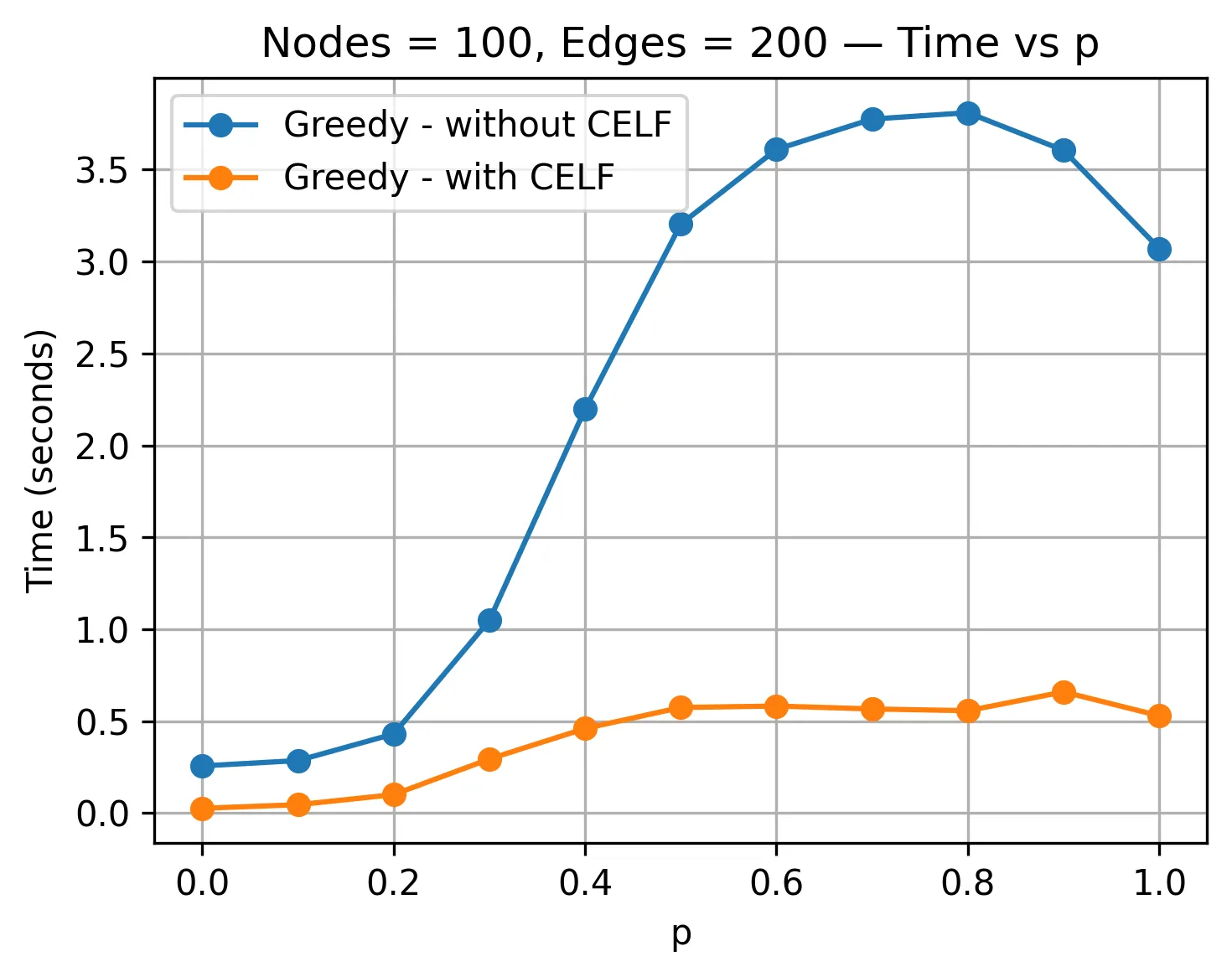
Given a network, the critical node detection problem finds a subset of nodes whose removal disrupts the network connectivity. Since many real-world systems are naturally modeled as graphs, assessing the vulnerability of the network is essential, with applications in transportation systems, traffic forecasting, epidemic control, and biological networks. In this paper, we consider a stochastic version of the critical node detection problem, where the existence of edges is given by certain probabilities. We propose heuristics and learning-based methods for the problem and compare them with existing algorithms. Experimental results performed on random graphs from small to larger scales, with edge-survival probabilities drawn from different distributions, demonstrate the effectiveness of the methods. Heuristic methods often illustrate the strongest results with high scalability, while learning-based methods maintain nearly constant inference time as the network size and density grow.
In this paper we deal with a subclass of chordal graphs, which are simultaneously strictly chordal and interval, the strictly interval graphs. We present a new characterization of the class that leads to a simple linear recognition algorithm. Next we introduce a new subclass of strictly interval graphs, the $SI$-core graphs, that are non-split and non-cograph graphs and show that several elements of the new class are Laplacian integral.
Determining the complexity of colouring ($4K_1, C_4$)-free graph is a long open problem. Recently Penev showed that there is a polynomial-time algorithm to colour a ($4K_1, C_4, C_6$)-free graph. In this paper, we will prove that if $G$ is a ($4K_1, C_4, P_6$)-free graph that contains a $C_6$, then $G$ has bounded clique-width. To this purpose, we use a new method to bound the clique-width, that is of independent interest. As a consequence, there is a polynomial-time algorithm to colour ($4K_1, C_4, P_6$)-free graphs.
 2512.00101
2512.00101We introduce a fun problem that can be considered as a variant of the classic birthday problem, the Bottleneck Birthday Problem (BBP). It is stated as: what is the maximum number of people we have to choose so that no day of the year has more than $r \geq 1$ birthdays incident on it with probability at least 1/2? We provide a survey of techniques used in the literature on occupancy and load balancing problems to derive recurrence relations for exact computation of the probability and the number of people, keeping probability fixed at a threshold. Further, we show that restricted Stirling numbers of the second kind can be used to derive an additional recurrence, in a novel way. We provide numerical results from an implementation of the recurrences.

This work presents conjectures about eigenvalues of matrices associated with $k$-path graphs, the algebraic connectivity, defined as the second smallest eigenvalue of the Laplacian matrix, and the $α$-index, as the largest eigenvalue of the $A_α$-matrix. For this purpose, a process based in Pereira et al., is presented to generate lists of $k$-path graphs containing all non-isomorphic 2-paths, 3-paths, and 4-paths of order $n$, for $6 \leq n \leq 26, 8 \leq n \leq 19$, and $10 \leq n \leq 18$, respectively. Using these lists, exhaustive searches for extremal graphs of fixed order for the mentioned eigenvalues were performed. Based on the empirical results, conjectures are suggested about the structure of extremal $k$-path graphs for these eigenvalues.
Given a language, which in this article is a set of strings of some fixed length, we study the problem of producing its elements by a procedure in which each position has its own local rule. We introduce a way of measuring how much communication is needed between positions. The communication structure is captured by a simplicial complex whose vertices are the positions and the simplices are the communication channels between positions. The main problem is then to identify the simplicial complexes that can be used to generate a given language. We develop the theory and apply it to a number of languages.
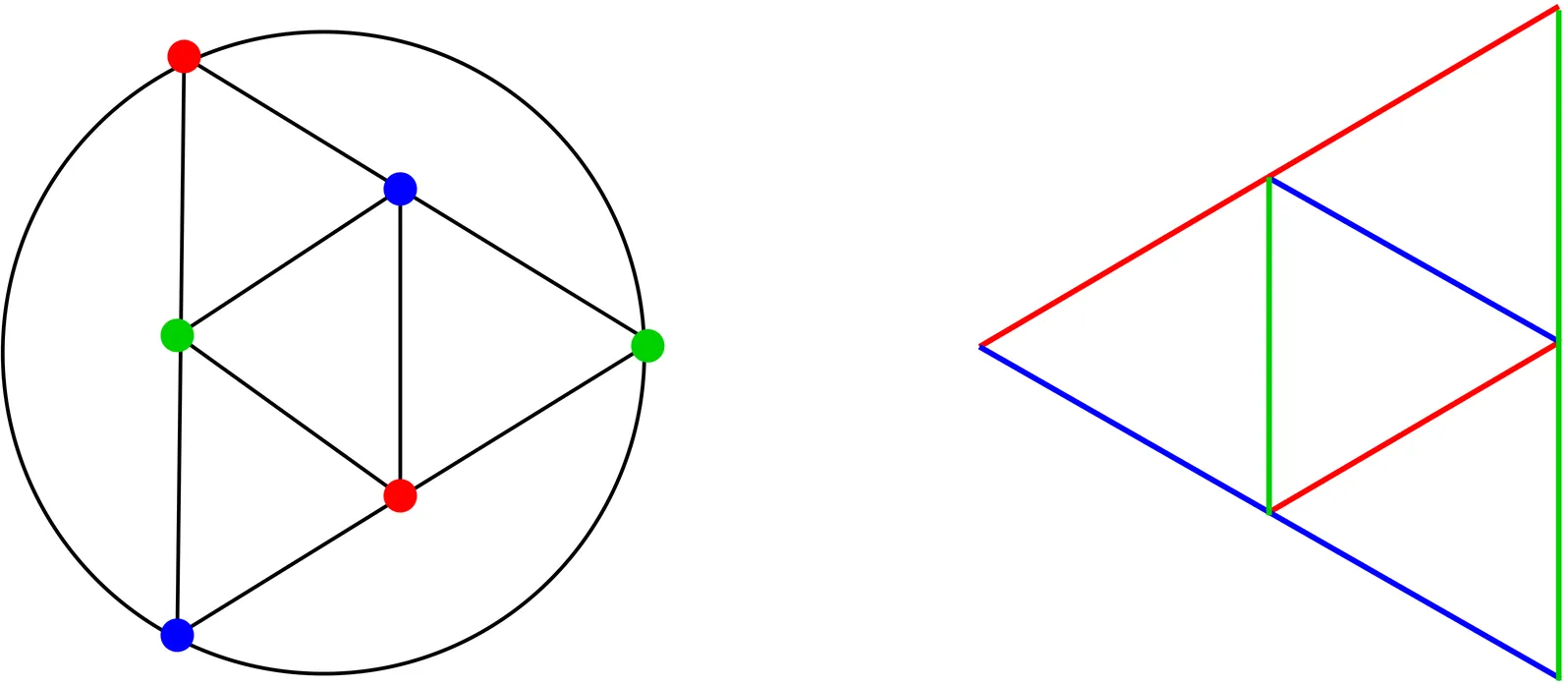
In his PhD Thesis, E.R. Scheinerman conjectured that planar graphs are intersection graphs of line segments in the plane. This conjecture was proved with two different approaches by J. Chalopin and the author, and by the author, L. Isenmann, and C. Pennarun. In the case of 3-colorable planar graphs E.R. Scheinerman conjectured that it is possible to restrict the set of slopes used by the segments to only 3 slopes. Here we prove this conjecture by using an approach introduced by S. Felsner to deal with contact representations of planar graphs with homothetic triangles.
Topological indices are graph-theoretic descriptors that play a crucial role in mathematical chemistry, capturing the structural characteristics of molecules and enabling the prediction of their physicochemical properties. A widely studied category of topological indices, known as degree-based topological indices, are calculated as the sum of the weights of a graph's edges, where each edge weight is determined by a formula that depends solely on the degrees of its endpoints. This work focuses exclusively on chemical graphs in which no vertex has a degree greater than 3, a model for conjugated systems. Within a polyhedral framework, each chemical graph is mapped to a point in a three-dimensional space, enabling extremal values of any degree-based topological index to be determined through linear optimization over the corresponding polyhedron. Analysis within this framework reveals that extremality is limited to a small subset of chemical graph families, implying that certain chemical graphs can never attain extremality for any degree-based topological index. The main objective of this paper is to present ChemicHull, an online tool we have developed to determine and display extremal chemical graphs for arbitrary degree-based topological indices. To illustrate the power of this tool, we easily recover established results, emphasizing its effectiveness for chemically significant graph classes such as chemical trees and unicyclic chemical graphs. This tool also enabled the identification of a counterexample to a previously published extremal result concerning the Randić index.
We investigate a process of joining $k$ random spanning trees on a fixed clique $K_n$. The joined trees may not be disjoint and multiple edges are replaced by one simple edge. This process produces a simple graph $G$ on $n$~vertices with an edge set, which is a union of edge sets of the joined trees. We study a random variable $S_{k}$ of the number of edges in the generated graph $G$. The exact formula is derived for the expected value of the random variable $S_{k}$. In addition, an upper bound on the concentration coefficient of the random variable $S_{k}$ is provided. We use results of our analysis to design an algorithm to generate $k$-edge connected graphs for arbitrarily large values of $k \geq 2$. The designed algorithm solves a particular case of the Survivable Network Design Problem, where the cost of each edge is $c_{e} = 1$ and the connectivity requirement for each pair of vertices $u, v \in V(G)$ is $k$.The proposed algorithm is within a factor strictly less than $2$ of the optimal value (i.e., the number of edges in the generated graph) and its running time is $O(kn\log{n})$.

The Graph Burning Problem (GBP) is a combinatorial optimization problem that has gained relevance as a tool for quantifying a graph's vulnerability to contagion. Although it is based on a very simple propagation model, its decision version is NP-complete, and its optimization version is NP-hard. Many of its theoretical properties across different graph families have been thoroughly explored, and numerous interesting variants have been proposed. This paper reports novel mathematical programs for the optimization version of the classical GBP. Among the presented programs are a Mixed-Integer Linear Program (MILP), a Constraint Satisfaction Problem (CSP), two Integer Linear Programs (ILP), and two Quadratic Unconstrained Binary Optimization (QUBO) problems. Most optimization solvers can handle these, being QUBO problems of a capital interest in quantum computing. The primary aim of this paper is to gain a comprehensive understanding of the GBP by examining its different formulations. Compared to other mathematical programs from the literature, the ones presented here are conceptually simpler and involve fewer variables. These make them more practical for finding optimal solutions using optimization algorithms and solvers, as we show by solving some instances with millions of vertices in just a few minutes.