Mathematical Finance
Derivatives pricing, portfolio theory, and financial mathematics
51 papers
2601.04900Uniqueness of invariant measures as a structural property of markov kernels
We identify indecomposability as a key measure-theoretic underlying uniqueness of invariant probability measures for discrete-time Markov kernels on general state spaces. The argument relies on the mutual singularity of distinct invariant ergodic measures and on the observation that uniqueness follows whenever all invariant probability measures are forced to charge a common reference measure. Once existence of invariant probability measures is known, indecomposability alone is sufficient to rule out multiplicity. On standard Borel spaces, this viewpoint is consistent with the classical theory: irreducibility appears as a convenient sufficient condition ensuring indecomposability, rather than as a structural requirement for uniqueness. The resulting proofs are purely measure-theoretic and do not rely on recurrence, regeneration, return-time estimates, or regularity assumptions on the transition kernel.
2601.04900Jan 2026
View
Forecasting the U.S. Treasury Yield Curve: A Distributionally Robust Machine Learning Approach
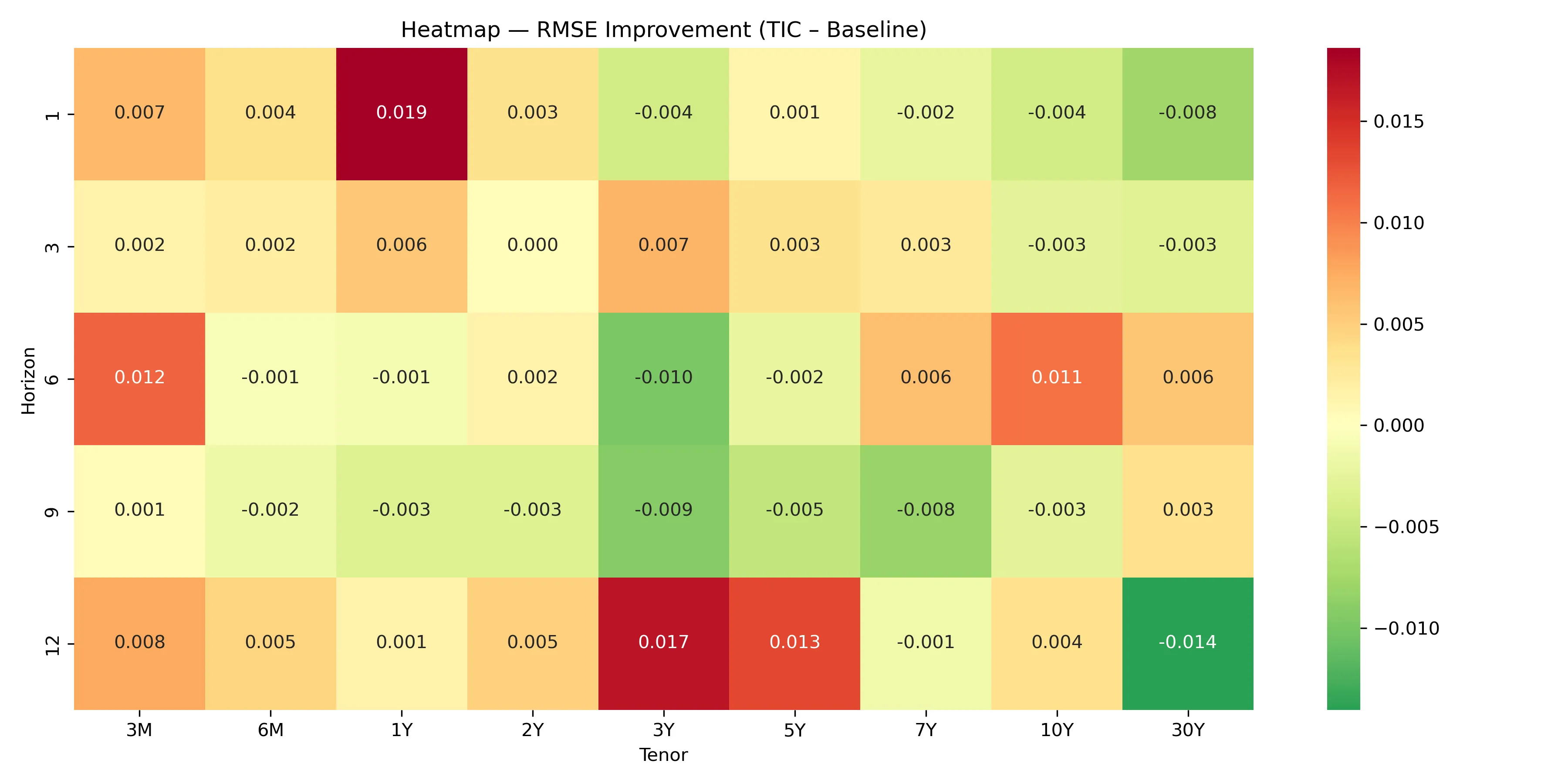
We study U.S. Treasury yield curve forecasting under distributional uncertainty and recast forecasting as an operations research and managerial decision problem. Rather than minimizing average forecast error, the forecaster selects a decision rule that minimizes worst case expected loss over an ambiguity set of forecast error distributions. To this end, we propose a distributionally robust ensemble forecasting framework that integrates parametric factor models with high dimensional nonparametric machine learning models through adaptive forecast combinations. The framework consists of three machine learning components. First, a rolling window Factor Augmented Dynamic Nelson Siegel model captures level, slope, and curvature dynamics using principal components extracted from economic indicators. Second, Random Forest models capture nonlinear interactions among macro financial drivers and lagged Treasury yields. Third, distributionally robust forecast combination schemes aggregate heterogeneous forecasts under moment uncertainty, penalizing downside tail risk via expected shortfall and stabilizing second moment estimation through ridge regularized covariance matrices. The severity of the worst case criterion is adjustable, allowing the forecaster to regulate the trade off between robustness and statistical efficiency. Using monthly data, we evaluate out of sample forecasts across maturities and horizons from one to twelve months ahead. Adaptive combinations deliver superior performance at short horizons, while Random Forest forecasts dominate at longer horizons. Extensions to global sovereign bond yields confirm the stability and generalizability of the proposed framework.
2601.04608Jan 2026
View2601.04096Sharp Transitions and Systemic Risk in Sparse Financial Networks
We study contagion and systemic risk in sparse financial networks with balance-sheet interactions on a directed random graph. Each institution has homogeneous liabilities and equity, and exposures along outgoing edges are split equally across counterparties. A linear fraction of institutions have zero out-degree in sparse digraphs; we adopt an external-liability convention that makes the exposure mapping well-defined without altering propagation. We isolate a single-hit transmission mechanism and encode it by a sender-truncated subgraph G_sh. We define adversarial and random systemic events with shock size k_n = c log n and systemic fraction epsilon n. In the subcritical regime rho_out < 1, we prove that maximal forward reachability in G_sh is O(log n) with high probability, yielding O((log n)^2) cascades from shocks of size k_n. For random shocks, we give an explicit fan-in accumulation bound, showing that multi-hit defaults are negligible with high probability when the explored default set is polylogarithmic. In the supercritical regime, we give an exact distributional representation of G_sh as an i.i.d.-outdegree random digraph with uniform destinations, placing it within the scope of the strong-giant/bow-tie theorem of Penrose (2014). We derive the resulting implication for random-shock systemic events. Finally, we explain why sharp-threshold machinery does not directly apply: systemic-event properties need not be monotone in the edge set because adding outgoing edges reduces per-edge exposure.
2601.04096Jan 2026
View2601.02276Forward Performance Processes under Multiple Default Risks
This article constructs a forward exponential utility in a market with multiple defaultable risks. Using the Jacod-Pham decomposition for random fields, we first characterize forward performance processes in a defaultable market under the default-free filtration. We then construct a forward utility via a system of recursively defined, indexed infinite-horizon backward stochastic differential equations (BSDEs) with discounting, and establish the existence, uniqueness, and boundedness of their solutions. To verify the required (super)martingale property of the performance process, we develop a rigorous characterization of this property with respect to the general filtration in terms of a set of (in)equalities relative to the default-free filtration. We further extend the analysis to a stochastic factor model with ergodic dynamics. In this setting, we derive uniform bounds for the Markovian solutions of the infinite-horizon BSDEs, overcoming technical challenges arising from the special structure of the system of BSDEs in the defaultable setting. Passing to the ergodic limit, we identify the limiting BSDE and relate its constant to the risk-sensitive long-run growth rate of the optimal wealth process.
2601.02276Jan 2026
View
Reinforcement Learning for Option Hedging: Static Implied-Volatility Fit versus Shortfall-Aware Performance
We extend the Q-learner in Black-Scholes (QLBS) framework by incorporating risk aversion and trading costs, and propose a novel Replication Learning of Option Pricing (RLOP) approach. Both methods are fully compatible with standard reinforcement learning algorithms and operate under market frictions. Using SPY and XOP option data, we evaluate performance along static and dynamic dimensions. Adaptive-QLBS achieves higher static pricing accuracy in implied volatility space, while RLOP delivers superior dynamic hedging performance by reducing shortfall probability. These results highlight the importance of evaluating option pricing models beyond static fit, emphasizing realized hedging outcomes.
2601.01709Jan 2026
View2601.01250European Options in Market Models with Multiple Defaults: the BSDE approach
We study non-linear Backward Stochastic Differential Equations (BSDEs) driven by a Brownian motion and p default martingales. The driver of the BSDE with multiple default jumps can take a generalized form involving an optional finite variation process. We first show existence and uniqueness. We then establish comparison and strict comparison results for these BSDEs, under a suitable assumption on the driver. In the case of a linear driver, we derive an explicit formula for the first component of the BSDE using an adjoint exponential semimartingale. The representation depends on whether the finite variation process is predictable or only optional. We apply our results to the problem of pricing and hedging a European option in a linear complete market with two defaultable assets and in a non-linear complete market with p defaultable assets. Two examples of the latter market model are provided: an example where the seller of the option is a large investor influencing the probability of default of a single asset and an example where the large seller's strategy affects the default probabilities of all p assets.
2601.01250Jan 2026
View
Stochastic factors can matter: improving robust growth under ergodicity
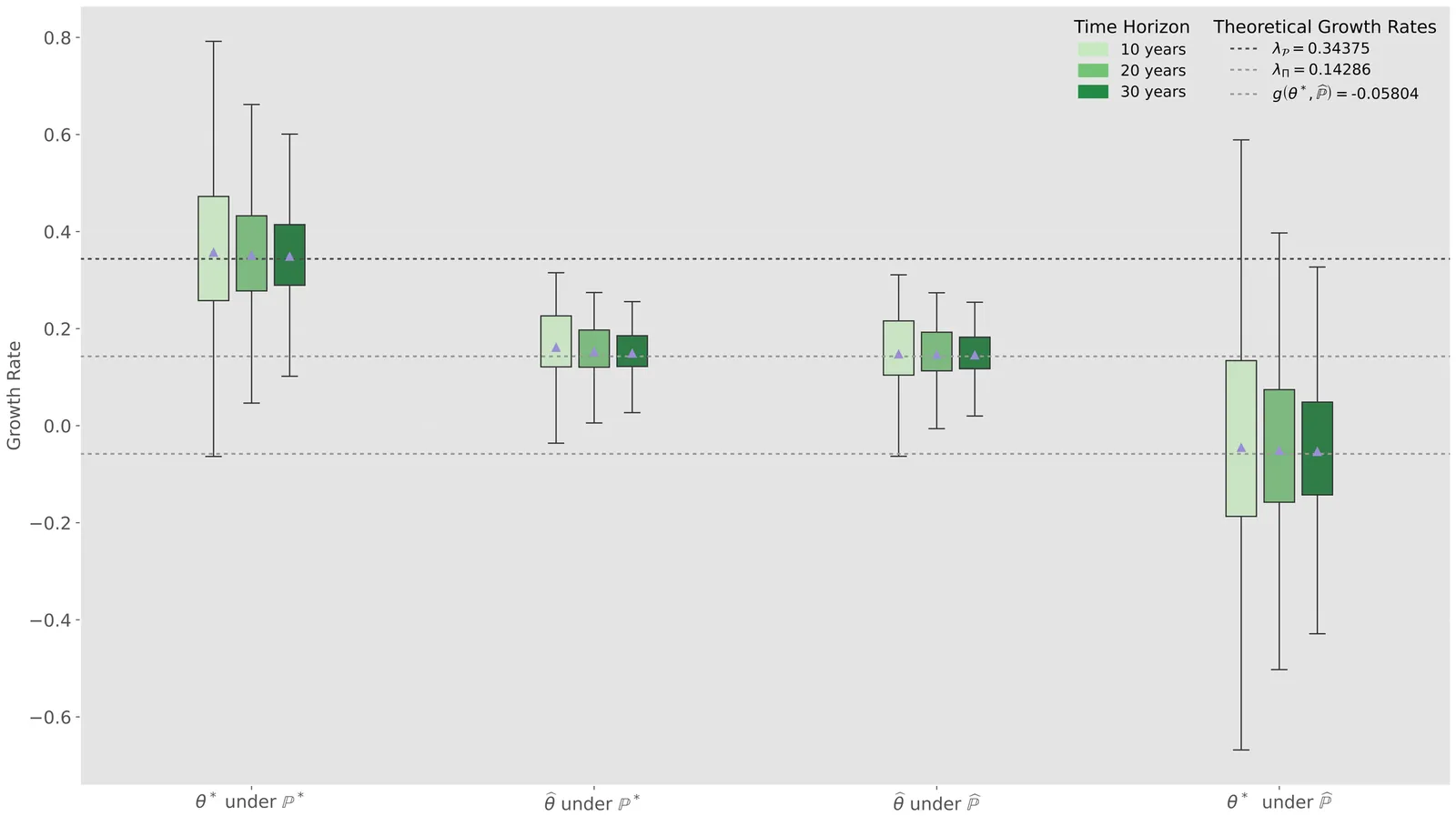
Drifts of asset returns are notoriously difficult to model accurately and, yet, trading strategies obtained from portfolio optimization are very sensitive to them. To mitigate this well-known phenomenon we study robust growth-optimization in a high-dimensional incomplete market under drift uncertainty of the asset price process $X$, under an additional ergodicity assumption, which constrains but does not fully specify the drift in general. The class of admissible models allows $X$ to depend on a multivariate stochastic factor $Y$ and fixes (a) their joint volatility structure, (b) their long-term joint ergodic density and (c) the dynamics of the stochastic factor process $Y$. A principal motivation of this framework comes from pairs trading, where $X$ is the spread process and models with the above characteristics are commonplace. Our main results determine the robust optimal growth rate, construct a worst-case admissible model and characterize the robust growth-optimal strategy via a solution to a certain partial differential equation (PDE). We demonstrate that utilizing the stochastic factor leads to improvement in robust growth complementing the conclusions of the previous study by Itkin et. al. (arXiv:2211.15628 [q-fin.MF], forthcoming in $\textit{Finance and Stochastics}$), which additionally robustified the dynamics of the stochastic factor leading to $Y$-independent optimal strategies. Our analysis leads to new financial insights, quantifying the improvement in growth the investor can achieve by optimally incorporating stochastic factors into their trading decisions. We illustrate our theoretical results on several numerical examples including an application to pairs trading.
2512.24906Dec 2025
View
Lambda Expected Shortfall
The Lambda Value-at-Risk (Lambda$-VaR) is a generalization of the Value-at-Risk (VaR), which has been actively studied in quantitative finance. Over the past two decades, the Expected Shortfall (ES) has become one of the most important risk measures alongside VaR because of its various desirable properties in the practice of optimization, risk management, and financial regulation. Analogously to the intimate relation between ES and VaR, we introduce the Lambda Expected Shortfall (Lambda-ES), as a generalization of ES and a counterpart to Lambda-VaR. Our definition of Lambda-ES has an explicit formula and many convenient properties, and we show that it is the smallest quasi-convex and law-invariant risk measure dominating Lambda-VaR under mild assumptions. We examine further properties of Lambda-ES, its dual representation, and related optimization problems.
2512.23139Dec 2025
View
Machine learning models for predicting catastrophe bond coupons using climate data
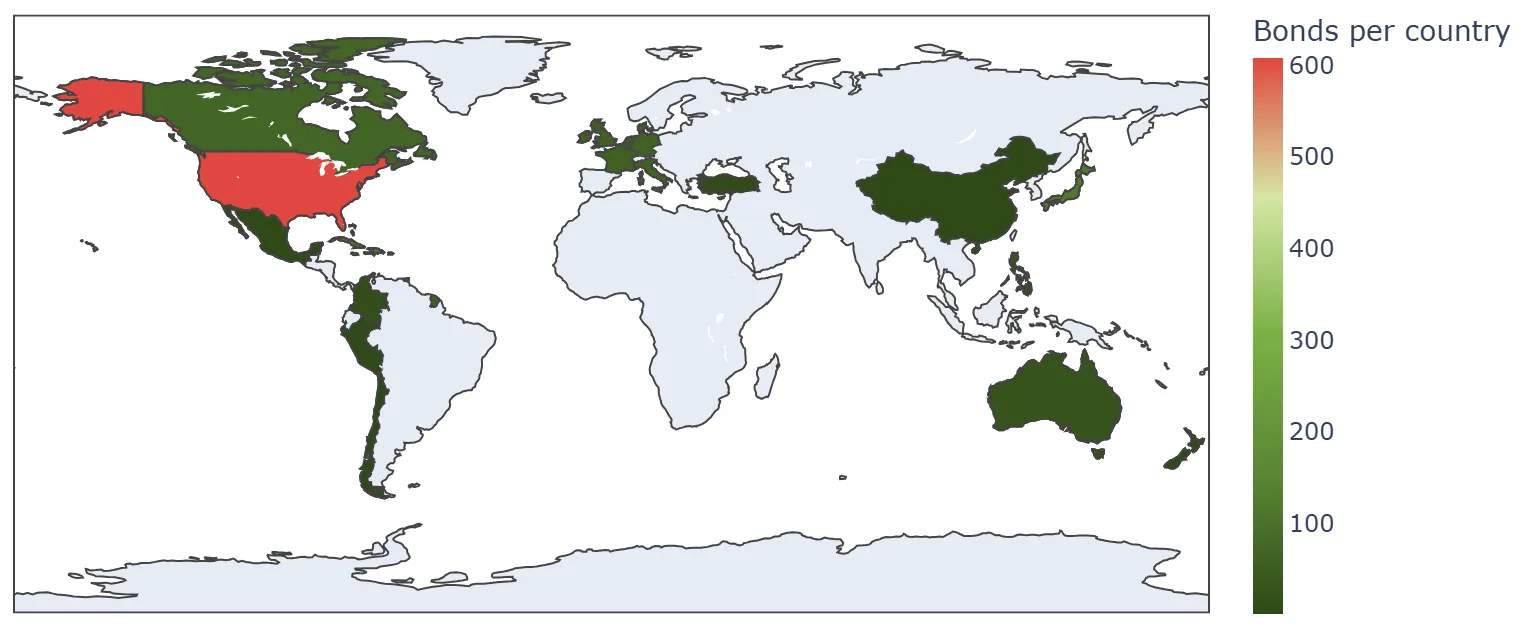
In recent years, the growing frequency and severity of natural disasters have increased the need for effective tools to manage catastrophe risk. Catastrophe (CAT) bonds allow the transfer of part of this risk to investors, offering an alternative to traditional reinsurance. This paper examines the role of climate variability in CAT bond pricing and evaluates the predictive performance of various machine learning models in forecasting CAT bond coupons. We combine features typically used in the literature with a new set of climate indicators, including Oceanic Ni{ñ}o Index, Arctic Oscillation, North Atlantic Oscillation, Outgoing Longwave Radiation, Pacific-North American pattern, Pacific Decadal Oscillation, Southern Oscillation Index, and sea surface temperatures. We compare the performance of linear regression with several machine learning algorithms, such as random forest, gradient boosting, extremely randomized trees, and extreme gradient boosting. Our results show that including climate-related variables improves predictive accuracy across all models, with extremely randomized trees achieving the lowest root mean squared error (RMSE). These findings suggest that large-scale climate variability has a measurable influence on CAT bond pricing and that machine learning methods can effectively capture these complex relationships.
2512.22660Dec 2025
View
Almost-Exact Simulation Scheme for Heston-type Models: Bermudan and American Option Pricing
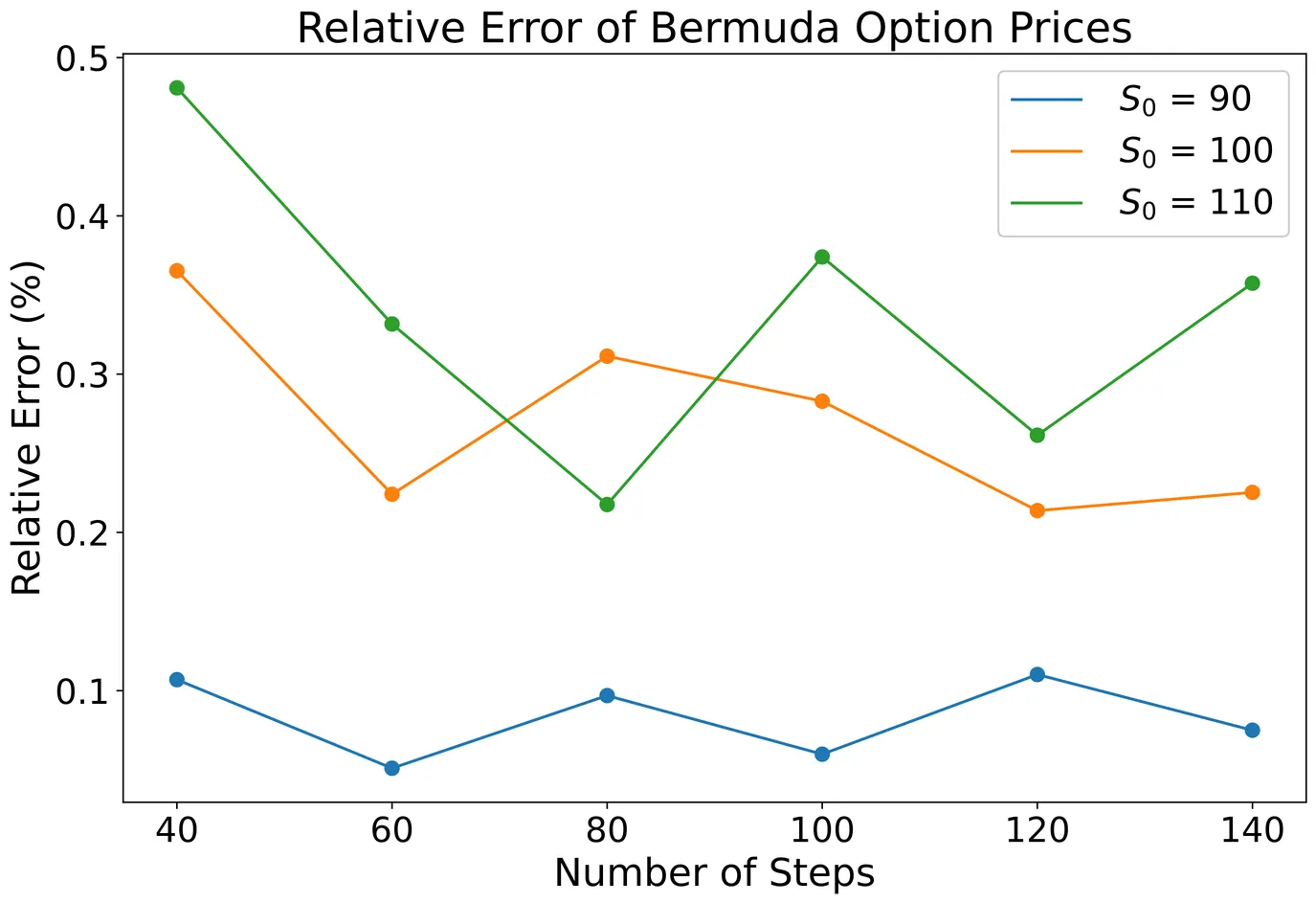
Recently, an Almost-Exact Simulation (AES) scheme was introduced for the Heston stochastic volatility model and tested for European option pricing. This paper extends this scheme for pricing Bermudan and American options under both Heston and double Heston models. The AES improves Monte Carlo simulation efficiency by using the non-central chi-square distribution for the variance process. We derive the AES scheme for the double Heston model and compare the performance of the AES schemes under both models with the Euler scheme. Our numerical experiments validate the effectiveness of the AES scheme in providing accurate option prices with reduced computational time, highlighting its robustness for both models. In particular, the AES achieves higher accuracy and computational efficiency when the number of simulation steps matches the exercise dates for Bermudan options.
2601.00815Dec 2025
View2512.17791Near-Maturity Asymptotics of Critical Prices of American Put Options under Exponential Lévy Models
In the present paper, we study the near-maturity ($t\rightarrow T^{-}$) convergence rate of the optimal early-exercise price $b(t)$ of an American put under an exponential Lévy model with a {\it nonzero} Brownian component. Two important settings, not previous covered in the literature, are considered. In the case that the optimal exercise price converges to the strike price ($b(T^{-})=K$), we contemplate models with negative jumps of unbounded variation (i.e., processes that exhibit high activity of negative jumps or sudden falls in asset prices). In the second case, when the optimal exercise price tend to a value lower than $K$, we consider infinite activity jumps (though still of bounded variations), extending existing results for models with finite jump activity (finitely many jumps in any finite interval). In both cases, we show that $b(T^{-})-b(t)$ is of order $\sqrt{T-t}$ with explicit constants proportionality. Furthermore, we also derive the second-order near-maturity expansion of the American put price around the critical price along a certain parabolic branch.
2512.17791Dec 2025
View2512.17702Relative arbitrage problem under eigenvalue lower bounds
We give a new formulation of the relative arbitrage problem from stochastic portfolio theory that asks for a time horizon beyond which arbitrage relative to the market exists in all ``sufficiently volatile'' markets. In our formulation, ``sufficiently volatile'' is interpreted as a lower bound on an ordered eigenvalue of the instantaneous covariation matrix, a quantity that has been studied extensively in the empirical finance literature. Upon framing the problem in the language of stochastic optimal control, we characterize the time horizon in question through the unique upper semicontinuous viscosity solution of a fully nonlinear elliptic partial differential equation (PDE). In a special case, this PDE amounts to the arrival time formulation of the Ambrosio-Soner co-dimension mean curvature flow. Beyond the setting of stochastic portfolio theory, the stochastic optimal control problem is analyzed for arbitrary compact, possibly non-convex, domains, thanks to a boundedness assumption on the instantaneous covariation matrix.
2512.17702Dec 2025
View
Interpretable Deep Learning for Stock Returns: A Consensus-Bottleneck Asset Pricing Model
We introduce the \textit{Consensus-Bottleneck Asset Pricing Model} (CB-APM), a partially interpretable neural network that replicates the reasoning processes of sell-side analysts by capturing how dispersed investor beliefs are compressed into asset prices through a consensus formation process. By modeling this ``bottleneck'' to summarize firm- and macro-level information, CB-APM not only predicts future risk premiums of U.S. equities but also links belief aggregation to expected returns in a structurally interpretable manner. The model improves long-horizon return forecasts and outperforms standard deep learning approaches in both predictive accuracy and explanatory power. Comprehensive portfolio analyses show that CB-APM's out-of-sample predictions translate into economically meaningful payoffs, with monotonic return differentials and stable long-short performance across regularization settings. Empirically, CB-APM leverages consensus as a regularizer to amplify long-horizon predictability and yields interpretable consensus-based components that clarify how information is priced in returns. Moreover, regression and GRS-based pricing diagnostics reveal that the learned consensus representations capture priced variation only partially spanned by traditional factor models, demonstrating that CB-APM uncovers belief-driven structure in expected returns beyond the canonical factor space. Overall, CB-APM provides an interpretable and empirically grounded framework for understanding belief-driven return dynamics.
2512.16251Dec 2025
View
Transfer Learning (Il)liquidity
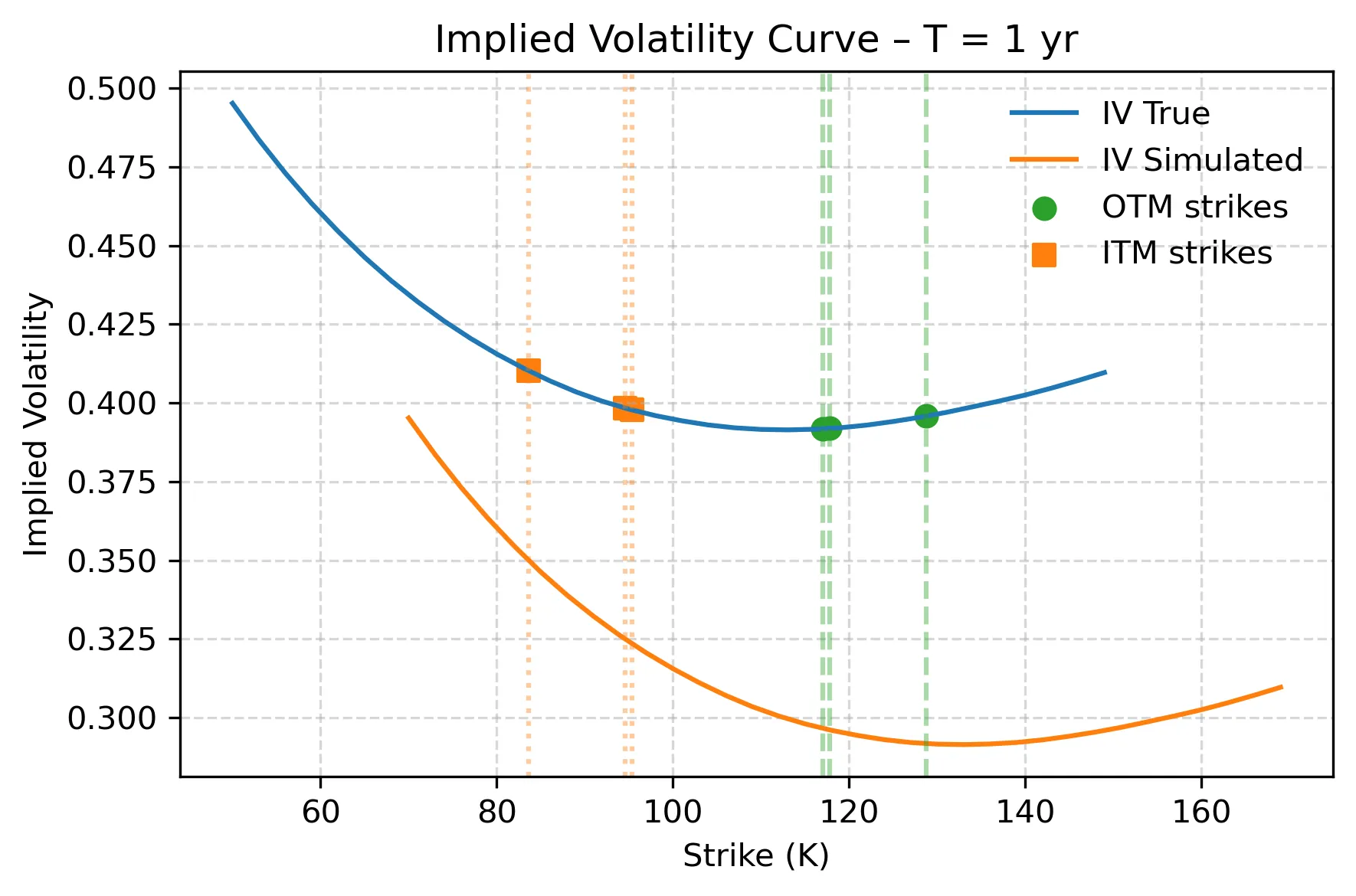
The estimation of the Risk Neutral Density (RND) implicit in option prices is challenging, especially in illiquid markets. We introduce the Deep Log-Sum-Exp Neural Network, an architecture that leverages Deep and Transfer learning to address RND estimation in the presence of irregular and illiquid strikes. We prove key statistical properties of the model and the consistency of the estimator. We illustrate the benefits of transfer learning to improve the estimation of the RND in severe illiquidity conditions through Monte Carlo simulations, and we test it empirically on SPX data, comparing it with popular estimation methods. Overall, our framework shows recovery of the RND in conditions of extreme illiquidity with as few as three option quotes.
2512.11731Dec 2025
View
Arbitrage-Free Option Price Surfaces via Chebyshev Tensor Bases and a Hamiltonian Fog Post-Fit
We study the construction of arbitrage-free option price surfaces from noisy bid-ask quotes across strike and maturity. Our starting point is a Chebyshev representation of the call price surface on a warped log-moneyness/maturity rectangle, together with linear sampling and no-arbitrage operators acting on a collocation grid. Static no-arbitrage requirements are enforced as linear inequalities, while the surface is fitted directly to prices via a coverage-seeking quadratic objective that trades off squared band misfit against spectral and transport-inspired regularisation of the Chebyshev coefficients. This yields a strictly convex quadratic program in the modal coefficients, solvable at practical scales with off-the-shelf solvers (OSQP). On top of the global backbone, we introduce a local post-fit layer based on a discrete fog of risk-neutral densities on a three-dimensional lattice (m,t,u) and an associated Hamiltonian-type energy. On each patch of the (m,t) plane, the fog variables are coupled to a nodal price field obtained from the baseline surface, yielding a joint convex optimisation problem that reweights noisy quotes and applies noise-aware local corrections while preserving global static no-arbitrage and locality. The method is designed such that for equity options panels, the combined procedure achieves high inside-spread coverage in stable regimes (in calm years, 98-99% of quotes are priced inside the bid-ask intervals) and low rates of static no-arbitrage violations (below 1%). In stressed periods, the fog layer provides a mechanism for controlled leakage outside the band: when local quotes are mutually inconsistent or unusually noisy, the optimiser allocates fog mass outside the bid-ask tube and justifies small out-of-band deviations of the post-fit surface, while preserving a globally arbitrage-free and well-regularised description of the option surface.
2512.01967Dec 2025
View
Stochastic Dominance Constrained Optimization with S-shaped Utilities: Poor-Performance-Region Algorithm and Neural Network
We investigate the static portfolio selection problem of S-shaped and non-concave utility maximization under first-order and second-order stochastic dominance (SD) constraints. In many S-shaped utility optimization problems, one should require a liquidation boundary to guarantee the existence of a finite concave envelope function. A first-order SD (FSD) constraint can replace this requirement and provide an alternative for risk management. We explicitly solve the optimal solution under a general S-shaped utility function with a first-order stochastic dominance constraint. However, the second-order SD (SSD) constrained problem under non-concave utilities is difficult to solve analytically due to the invalidity of Sion's maxmin theorem. For this sake, we propose a numerical algorithm to obtain a plausible and sub-optimal solution for general non-concave utilities. The key idea is to detect the poor performance region with respect to the SSD constraints, characterize its structure and modify the distribution on that region to obtain (sub-)optimality. A key financial insight is that the decision maker should follow the SD constraint on the poor performance scenario while conducting the unconstrained optimal strategy otherwise. We provide numerical experiments to show that our algorithm effectively finds a sub-optimal solution in many cases. Finally, we develop an algorithm-guided piecewise-neural-network framework to learn the solution of the SSD problem, which demonstrates accelerated convergence compared to standard neural network approaches.
2512.00299Nov 2025
View
Efficient Importance Sampling under Heston Model: Short Maturity and Deep Out-of-the-Money Options
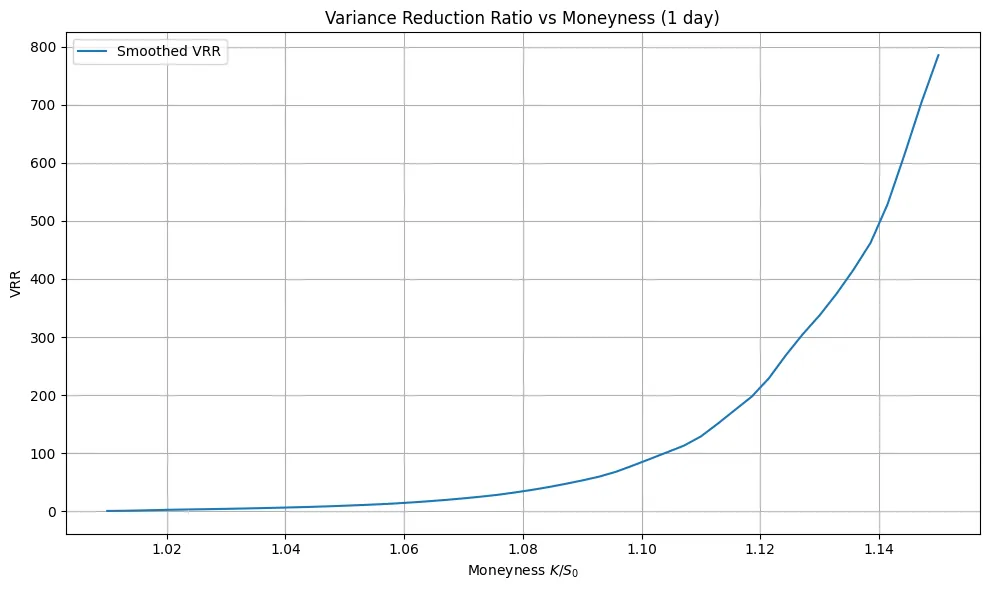
This paper investigates asymptotically optimal importance sampling (IS) schemes for pricing European call options under the Heston stochastic volatility model. We focus on two distinct rare-event regimes where standard Monte Carlo methods suffer from significant variance deterioration: the limit as maturity approaches zero and the limit as the strike price tends to infinity. Leveraging the large deviation principle (LDP), we design a state-dependent change of measure derived from the asymptotic behavior of the log-price cumulant generating functions. In the short-maturity regime, we rigorously prove that our proposed IS drift, inspired by the variational characterization of the rate function, achieves logarithmic efficiency (asymptotic optimality) by minimizing the decay rate of the second moment of the estimator. In the deep OTM regime, we introduce a novel slow mean-reversion scaling for the variance process, where the mean-reversion speed scales as the inverse square of the small-noise parameter (defined as the reciprocal of the log-moneyness). We establish that under this specific scaling, the variance process contributes non-trivially to the large deviation rate function, requiring a specialized Riccati analysis to verify optimality. Numerical experiments demonstrate that the proposed method yields substantial variance reduction--characterized by factors exceeding several orders of magnitude--compared to standard estimators in both asymptotic regimes.
2511.19826Nov 2025
View
Arbitrage-Free Bond and Yield Curve Forecasting with Neural Filters under HJM Constraints
We develop an arbitrage-free deep learning framework for yield curve and bond price forecasting based on the Heath-Jarrow-Morton (HJM) term-structure model and a dynamic Nelson-Siegel parameterization of forward rates. Our approach embeds a no-arbitrage drift restriction into a neural state-space architecture by combining Kalman, extended Kalman, and particle filters with recurrent neural networks (LSTM/CLSTM), and introduces an explicit arbitrage error regularization (AER) term during training. The model is applied to U.S. Treasury and corporate bond data, and its performance is evaluated for both yield-space and price-space predictions at 1-day and 5-day horizons. Empirically, arbitrage regularization leads to its strongest improvements at short maturities, particularly in 5-day-ahead forecasts, increasing market-consistency as measured by bid-ask hit rates and reducing dollar-denominated prediction errors.
2511.17892Nov 2025
View
Selective Forgetting in Option Calibration: An Operator-Theoretic Gauss-Newton Framework
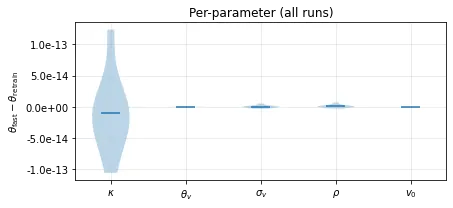
Calibration of option pricing models is routinely repeated as markets evolve, yet modern systems lack an operator for removing data from a calibrated model without full retraining. When quotes become stale, corrupted, or subject to deletion requirements, existing calibration pipelines must rebuild the entire nonlinear least-squares problem, even if only a small subset of data must be excluded. In this work, we introduce a principled framework for selective forgetting (machine unlearning) in parametric option calibration. We provide stability guarantees, perturbation bounds, and show that the proposed operators satisfy local exactness under standard regularity assumptions.
2511.14980Nov 2025
View
A Deep Learning-Based Method for Fully Coupled Non-Markovian FBSDEs with Applications
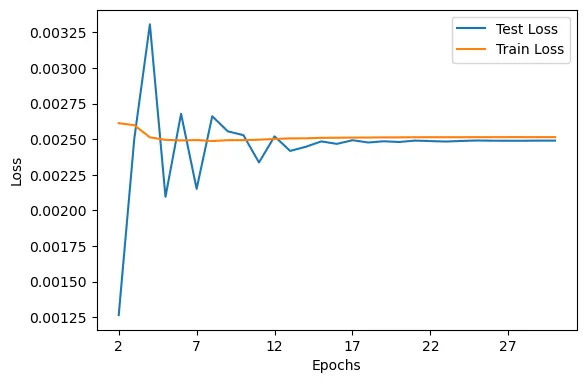
In this work, we extend deep learning-based numerical methods to fully coupled forward-backward stochastic differential equations (FBSDEs) within a non-Markovian framework. Error estimates and convergence are provided. In contrast to the existing literature, our approach not only analyzes the non-Markovian framework but also addresses fully coupled settings, in which both the drift and diffusion coefficients of the forward process may be random and depend on the backward components $Y$ and $Z$. Furthermore, we illustrate the practical applicability of our framework by addressing utility maximization problems under rough volatility, which are solved numerically with the proposed deep learning-based methods.
2511.08735Nov 2025
ViewPage 1 of 3