Number Theory

Algebraic and analytic number theory, arithmetic geometry

Trending in Number Theory

2601.01242

Averages of Arithmetic Functions over Conductors of Function Fields

For a finite group $G$ and a sufficiently large (but fixed) prime power $q$ coprime to $G$ we obtain asymptotics for the number of regular Galois extensions $L/ \mathbb{F}_q(t)$, with $\mathrm{Gal}(L/\mathbb{F}_q(t)) \cong G$, ramified at a single place of $\mathbb{F}_q(t)$, thus making progress on a positive characteristic analog of the Boston--Markin conjecture. We also obtain similar results for other arithmetic functions of the product of places of $\mathbb{F}_q(t)$ ramified in $L$, and for more general one-variable function fields over $\mathbb{F}_q$ in place of $\mathbb{F}_q(t)$. Some of our proofs make crucial use of a series of recent breakthroughs by Landesman--Levy, as well as a new `vanishing of stable homology in a given direction' result for representations of braid groups arising from braided vector spaces. Other inputs include a study of (rings of coinvariants of) braided vector spaces associated to racks with $2$-cocycles, a connection between convolution of arithmetic functions and direct sums of braided vector spaces, and a Goursat lemma for racks.

2601.012421

Jan 2026Number Theory

2512.20461

A classification of even representations onto 3-adic SL(2)

This paper gives a classification of even representations onto $\operatorname{SL}(2,\mathbb{Z}_3)$ of prime conductor. In addition, an explicit algorithm based on global class field theory is exhibited, computing an exhaustive series of such even representations.

2512.204613

Dec 2025Number Theory

2512.20413

Parameters of solvable automorphic forms

In a letter from Tate to Serre dated March 26, 1974, Tate suggested a classification of weight one modular forms of prime level in terms of their associated odd Artin representations. This paper carries out an analogous classification of Maass wave forms of prime power level in terms of complex even representations. The parameters are identified with techniques from class field theory and Galois representations. The classification reveals that there exist distinct Maass cusp forms of tetrahedral type on $Γ_1(\ell)$ that remain inequivalent modulo $3$ for $\ell = 7687, 16363$ and $20887$, and that these $\ell$ are the three smallest such primes.

2512.204133

Dec 2025Number Theory

2512.19076

On Factoring and Power Divisor Problems via Rank-3 Lattices and the Second Vector

We propose a deterministic algorithm based on Coppersmith's method that employs a rank-3 lattice to address factoring-related problems. An interesting aspect of our approach is that we utilize the second vector in the LLL-reduced basis to avoid trivial collisions in the Baby-step Giant-step method, rather than the shortest vector as is commonly used in the literature. Our results are as follows: 1. Compared to the result by Harvey and Hittmeir (Math. Comp. 91 (2022), 1367 - 1379), who achieved a complexity of O( N^(1/5) log^(16/5) N / (log log N)^(3/5)) for factoring a semiprime N = pq, we demonstrate that in the balanced p and q case, the complexity can be improved to O( N^(1/5) log^(13/5) N / (log log N)^(3/5) ). 2. For factoring sums and differences of powers, that is, numbers of the form N = a^n plus or minus b^n, we improve Hittmeir's result (Math. Comp. 86 (2017), 2947 - 2954) from O( N^(1/4) log^(3/2) N ) to O( N^(1/5) log^(13/5) N ). 3. For the problem of finding r-power divisors, that is, finding all integers p such that p^r divides N, Harvey and Hittmeir (Proceedings of ANTS XV, Research in Number Theory 8 (2022), no. 4, Paper No. 94) recently directly applied Coppersmith's method and achieved a complexity of O( N^(1/(4r)) log^(10+epsilon) N / r^3 ). By using faster LLL-type algorithms and sieving on small primes, we improve their result to O( N^(1/(4r)) log^(7+3 epsilon) N / ((log log N minus log(4r)) r^(2+epsilon)) ). The worst-case running time for their algorithm occurs when N = p^r q with q on the order of N^(1/2). By focusing on this case and employing our rank-3 lattice approach, we achieve a complexity of O( r^(1/4) N^(1/(4r)) log^(5/2) N ). In conclusion, we offer a new perspective on these problems, which we hope will provide further insights.

2512.190761

Dec 2025Number Theory

2512.18581

Trigonometric Determinants via special values of Dirichlet $L$-Functions

In this paper, we investigate the determinants involving some trigonometric functions. We establish a connection between these determinants and the special values of Dirichlet L-functions, thereby extending Guo's results to arbitrary positive integers n. In addition, we also prove a conjecture raised by Zhi-Wei Sun. Our main tool is the spectral decomposition of some linear operators. By the same method we obtain an explicit formula for the determinants of sine matrices. This formula is expressed as a product of Gauss sums attached to Dirichlet characters.

2512.185811

Dec 2025Number Theory

2512.16358

Counting appearances of integers in sets of arithmetic progressions

The sequence $A067549$ of The On-Line Encyclopedia of Integer Sequences is defined as $(a_k)_{k \geq 1}$ with $a_k$ being the determinant of the $k \times k$ matrix whose diagonal contains the first $k$ prime numbers and all other elements are ones. We relate this sequence to a concrete counting problem. Choose an arbitrary residue class $r_i$ for each prime $p_i$ with $1 \leq i \leq k$ and set $P_k = \prod_{i=1}^k p_i$. We show that $a_k$ is the number of integers in $[1, P_k]$ that are contained in \emph{at most} one of the $k$ chosen residue classes. Interestingly, we show that this sequence is closely related to the better known sequence $A005867$ for which we derive a novel characterisation in terms of determinants and which gives the number of integers in $[1, P_k]$ that are not contained in any of the $k$ residue classes. Our proof is purely structural and, therefore, it can be generalised to counting appearances of integers in residue classes of arbitrary arithmetic progressions generated by $k$ different primes using the determinant of a matrix of ones having those $k$ primes on its diagonal. The revealed structure also offers a fast way of calculating such determinants.

2512.163581

Dec 2025Number Theory

2512.16118

Equidistribution of polynomial sequences in function fields: resolution of a conjecture

Let $\mathbb F_q$ be the finite field of $q$ elements having characteristic $p$, and denote by $\mathbb K_\infty=\mathbb F_q((1/t))$ the field of formal Laurent series in $1/t$. We consider the equidistribution in $\mathbb T=\mathbb K_\infty/\mathbb F_q[t]$ of the values of polynomials $f(u)\in \mathbb K_\infty [u]$ as $u$ varies over $\mathbb F_q[t]$. Let $\mathcal K$ be a finite set of positive integers, and suppose that $α_r\in \mathbb K_\infty$ for $r\in \mathcal K\cup \{0\}$. We show that the polynomial $\sum_{r\in \mathcal K\cup\{0\}}α_ru^r$ is equidistributed in $\mathbb T$ whenever $α_k$ is irrational for some $k\in \mathcal K$ satisfying $p\nmid k$, and also $p^vk\not\in \mathcal K$ for any positive integer $v$. This conclusion resolves in full a conjecture made jointly by the third, fourth and fifth authors.

2512.161181

Dec 2025Number Theory

2512.14247

On the local equivariant Tamagawa number conjecture for Tate motives

The local equivariant Tamagawa number conjecture (local ETNC) for a motive predicts a precise relationship between the local arithmetic complex and the root numbers which appear in the (conjectural) functional equations of the $L$-functions. In this paper, we prove the local ETNC for the Tate motives under a certain unramified condition at $p$. Our result gives a generalization of the previous works by Burns--Flach and Burns--Sano. Our strategy basically follows those works and builds upon the classical theory of Coleman maps and its generalization by Perrin-Riou.

2512.142471

Dec 2025Number Theory

2512.11337

On the rational approximation to linear combinations of powers

For a complex number $x$, $\Vert x\Vert:=\min\{|x-m|:m\in\mathbb{Z}\}$. Let $k\geq 1$ be an integer, and $K$ be a number field. Let $α_1,\ldots,α_k$ be algebraic numbers with $|α_i|\geq 1$ and let $d_i$ denotes the degree of $α_i$ for $1\leq i\leq k$. Set $d=d_1+\cdots+d_k$. In this article, we show that if the inequality $ 0<\Vertλ_1 qα^n_1+\cdots+λ_k qα^n_k\Vert<\frac{θ^n}{q^{d+\varepsilon}} $ has infinitely many solutions in $(n, q,λ_1,\ldots,λ_k)\in \mathbb{N}^2\times (K^\times)^k$ with absolute logarithmic Weil height of $λ_i$ is small compared to $n$ and some $θ\in (0,1)$, then, in particular, the tuple $(λ_1 qα^n_1,\ldots, λ_k qα^n_k)$ is pseudo-Pisot, and at least one of $α_i$ is an algebraic integer. This result can be viewed as Roth's type theorem for linear combinations of powers of algebraic numbers over $\overline{\mathbb{Q}}$. The case $q=1$ was recently proved by Kulkarni, Mavraki, and Nguyen \cite{kul}, which is a generalization of Mahler's question proved in \cite{corv}. As a consequence of our result, we obtain the following generalization of this question: let $α>1$ be an algebraic number with $d=[\mathbb{Q}(α):\mathbb{Q}]$. For a given $\varepsilon>0$, if the inequality $$ 0<\Vertλqα^n\Vert<\frac{θ^n}{q^{d+\varepsilon}} $$ has infinitely many solutions in the tuples $(n,q,λ)\in \mathbb{N}^2\times K^\times$ with absolute logarithmic Weil height of $λ$ is small compared to $n$ and $θ\in (0,1)$, then some power of $α$ is a Pisot number. As an application of this result, we deduce the transcendence of certain infinite products of algebraic numbers.

2512.113371

Dec 2025Number Theory

2512.11217

Improved Bounds for the Freiman-Ruzsa Theorem

Let $A$ be a finite subset of an abelian group $G$, and suppose that $|A+A|\leq K|A|$. We show that for any $ε>0$, there exists a constant $C_ε$ such that $A$ can be covered by at most $\exp(C_ε\log(2K)^{1+ε})$ translates of a convex coset progression with dimension at most $C_ε\log(2K)^{1+ε}$ and size at most $\exp(C_ε\log(2K)^{1+ε})|A|$. This falls just short of the Polynomial Freiman-Ruzsa conjecture, which asserts that this statement is true for $ε=0$, and improves on results of Sanders and Konyagin, who showed that this statement is true for all $ε>2$. To prove this result, we use a mixture of entropy methods and Fourier analysis.

2512.112171

Dec 2025Number Theory

2512.10661

A purity theorem for Mahler equations

The principal aim of this paper is to establish a purity theorem for Mahler functions that is reminiscent of famous purity theorems for G-functions by D. and G. Chudnovsky and for E-functions (and, more generally, for holonomic arithmetic Gevrey series) by Y. Andr{é}. Our approach is based on a preliminary study of independent interest of the nature of the solutions of Mahler equations. Roughly speaking, we prove a reduction result for Mahler systems, implying that any Mahler equation admits a complete basis of solutions formed of what we call generalized Mahler series. These are sums involving Puiseux series, Hahn series of a very special type and solutions of inhomogeneous equations of order 1 with constant coefficients. In the light of B. Adamczewski, J. P. Bell and D. Smertnig's recent height gap theorem, we introduce a natural filtration on the set of generalized Mahler series according to the arithmetic growth of the coefficients of the Puiseux series involved in their decomposition. This filtration has five pieces. Our purity theorem states that the membership of a generalized Mahler series to one of the three largest pieces of this filtration propagates to any other generalized Mahler series solution of its minimal Mahler equation. We also show that this statement does not extend to the smallest two pieces.

2512.106611

Dec 2025Number Theory

2512.05095

On the Outer Automorphism Groups of the Absolute Galois Groups of 2-adic local Fields

In the present paper, we study the outer automorphism groups of the absolute Galois groups of 2-adic local fields from the point of view of anabelian geometry. Let us recall that it is well-known that the natural homomorphism from the automorphism group of a mixed-characteristic local field to the outer automorphism group of the absolute Galois group of the given mixed-characteristic local field is injective. Moreover, Hoshi and the author of the present paper proved that, for absolutely abelian mixed-characteristic local fields with odd residue characteristic $p$ and even extension degree over ${\mathbb Q}_p$, this subgroup arising from field automorphisms is not normal in the outer automorphism group and has infinitely many distinct conjugates. As a result in this direction, one of the main results of the present paper is the assertion that if a 2-adic local field satisfies certain conditions, then the set of conjugates of the subgroup arising from field automorhisms in the outer automorphism group is infinite, which thus implies that this subgroup is not normal in the outer automorphism group. On the other hand, for an odd prime number $p$, Hoshi proved the existence of an irreducible Hodge-Tate $p$-adic representation of dimension two of the absolute Galois group of a $p$-adic local field and an automorphism of the absolute Galois group such that the $p$-adic Galois representation obtained by pulling back the given $p$-adic Galois representation by the given automorphism is not Hodge-Tate. As a result in a direction that is different from the above direction, another main result of the present paper is the existence of a pair of a representation and an automorphism that is similar to the above pair in the case where $p=2$.

2512.050951

Dec 2025Number Theory

2512.03481

The $p$-adic Valuations of Möbius Duals of Lucas Sequences

In this paper, we extend the $p$-adic valuations of the Möbius duals of Lucas sequences, originally obtained by Carmichael for regular Lucas sequences to irregular Lucas sequences. We conclude with a brief observation about the relationship of these valuations to the existence of Wall-Sun-Sun primes.

2512.034811

Dec 2025Number Theory

2512.02927

Eisenstein cohomology and congruences for the ratios of Rankin--Selberg $L$-functions

A well-known principle states that a congruence between objects should give rise to a corresponding congruence between the special values of $L$-functions attached to these objects. In this article, using the machinery of Eisenstein cohomology after refining it for integral cohomology, we prove an instance of this principle for the ratios of critical values for Rankin--Selberg $L$-functions attached to pairs of holomorphic cuspforms.

2512.029271

Dec 2025Number Theory

2512.02919

Congruences for the ratios of Rankin--Selberg $L$-functions

A well-known principle states that a congruence between objects should give rise to a corresponding congruence between the special values of $L$-functions attached to these objects. In this article we computationally investigate this principle for Rankin--Selberg $L$-functions attached to pairs of holomorphic cuspforms.

2512.029191

Dec 2025Number Theory

2511.21171

Evaluation of Bianchi Rigid Meromorphic Cocycles at Big ATR Points

We develop the tools required to effectively evaluate the Bianchi rigid meromorphic cocycles introduced by Darmon-Gehrmann-Lipnowski at big ATR points, and use them to obtain the first numerical verification of the conjectured algebraicity of these special values. Moreover, our computations suggest that these special values exhibit behaviour analogous to that of the special values of Borcherds products on Hilbert modular surfaces at big CM points.

2511.211711

Nov 2025Number Theory

2511.20829

Partition-theoretic model of prime distribution, II

In recent work by Botkin, Dawsey, Hemmer, Just and the present author, a deterministic model of prime number distribution is developed based on properties of integer partitions that gives almost exact estimates for $π(n)$, the number of primes less than or equal to positive integer $n$, up to $n=10{,}000$. In this follow-up paper, the author summarizes the ideas behind this partition-theoretic model of primes and formulates a computational model that is practically exact in its estimates of $π(n)$ up to $n=100,000$.

2511.208291

Nov 2025Number Theory

Fermat near misses and the integral Hilbert Property

We consider the Diophantine equation $x^4 + y^4 - w^2 = n$ for $n \in \mathbb{Z}$, which is related to near misses for the quartic case of Fermat's Last Theorem. For certain $n$ we show that the set of solutions is infinite, or more generally not thin. Our approach is via the geometry of del Pezzo surfaces of degree $2$, and we prove a more general result on non-thinness of integral points on double conic bundle surfaces.

2511.174562

Nov 2025Number Theory

The Landau-Selberg-Delange method for products of Dirichlet $L$-functions, and applications, I

The Landau-Selberg-Delange method gives precise asymptotic formulas for the partial sums $\sum_{n \le x} \, a_n$ of a Dirichlet series $\sum_n \, a_n/n^s$ that behaves like a complex power of the Riemann zeta function. However, situations often arise when the Dirichlet series behaves like a product of complex powers of several Dirichlet $L$-functions to a modulus $q$. In such situations, one often requires sharp asymptotic formulas for the partial sums $\sum_{n \le x} \, a_n$ that apply in much wider ranges of $q$ than permitted by known forms of the Landau-Selberg-Delange method. In this manuscript, we address this problem, giving new estimates on $\sum_{n \le x} \, a_n$ in ranges of $q$ that are (in most applications) much wider than attainable from previous results. Our results also weaken certain hypotheses on the size of $\{a_n\}_n$. As applications of our main theorems, we extend Landau's classical results on the distribution of integers with prime factors restricted to progressions, and improve upon Chang, Martin and Nguyen's work on the distributions of the least invariant factors and least primary factors of multiplicative groups. We also extend the classical Sathe-Selberg theorem and study the local laws of the functions $Ω_a(n)$ and $ω_a(n)$, that count (with and without multiplicity, respectively), the number of prime divisors of $n$ lying in the progression $a$ mod $q$.

2511.159281

Nov 2025Number Theory

Computational study of irrational rotations via exact discontinuity tracking

The discrepancy sum $D_N(x,ρ)$ for irrational rotations has been of interest to mathematicians for over a century. While historically studied in an ``almost-everywhere'' or asymptotic sense, $D_N$ for finite N is increasingly an object of interest for its nontrivial properties that depend on the Diophantine properties of $ρ$. This behavior is periodic in N with respect to the quotients of the continued fraction convergents, which grow quickly for some irrationals. Thus the stable computation of the sum is necessary for forming conjectures about its properties. However, computing the exact value of the sum and its corresponding probability density function (pdf) is notoriously difficult due to numerical instability in the sum itself and the failure of sampling methods to capture its jump discontinuities. This paper presents a novel computational algorithm that fully defines the discrepancy function and its associated pdf through its discontinuities. This allows the calculation of $D_N(x,ρ)$ to machine precision with minimal storage in O(N) time. This vast improvement in computability over the O(N^2) naive version enables, for the first time, the direct computation of the exact pdf up to machine precision in O(N log N) time, and with it, key properties of the discrepancy: $ \|D_N \|_{\infty}$ (half of the support of the pdf), $ \|D_N \|_{2}^2$ (the variance of the pdf), and the kurtosis of the pdf. A key strength of the algorithm lies in its ability to produce clear, exact figures, allowing the development of mathematical intuition and the quick testing of conjectures. As an example, a newly conjectured pattern is presented: when $ρ$ is well-approximated by rational $\frac{p_n}{q_n}$, the pdf exhibits a predictable spiked-trapezoidal pattern when $N=kq_n$. These shapes degrade as $k$ increases, at a speed depending on how well $\frac{p_n}{q_n}$ approximates $ρ$.

2511.138791

Nov 2025Number Theory

1,391 papers

2601.05189

Distibution of values of higher derivatives of $L'(s,χ)/L(s,χ)$

In this article we study the value distribution theory for the first derivative of the logarithmic derivative of Dirichlet $L$-functions, generalizing certain results of Ihara, Matsumoto et. al. related to ``$M$-functions" for $σ= $ Re$(s) > 1$. We then discuss how things evolve for higher derivatives.

2601.05189Jan 2026

View

2601.05133

On non-Archimedean quantum mathematics and non-Archimedean (quantum) computation

We consider selected aspects of (non-Archimedean) quantum mathematics and non-Archimedean (quantum) computation.

2601.05133Jan 2026

View

2601.05121

Strong paucity in the Brüdern-Robert Diophantine system

Let $k$ be a natural number with $k\ge 2$, and let $\varepsilon>0$. We consider the number $V_k^*(P)$ of integral solutions of the system of simultaneous Diophantine equations \[ x_1^{2j-1}+\ldots +x_{k+1}^{2j-1}=y_1^{2j-1}+\ldots +y_{k+1}^{2j-1}\quad (1\le j\le k), \] with $1\le x_i,y_i\le P$ $(1\le i\le k+1)$. Writing $L_k^*(P)$ for the number of diagonal solutions with $\{x_1,\ldots ,x_{k+1}\}=\{y_1,\ldots ,y_{k+1}\}$, so that $L_k^*(P)\sim (k+1)!P^{k+1}$, we prove that \[ V_k^*(P)-L_k^*(P)\ll P^{\sqrt{8k+9}-1+\varepsilon}. \] This establishes a strong paucity result improving on earlier work of Brüdern and Robert.

2601.05121Jan 2026

View

2601.05024

Residue Theorem, Regularization and Parity Theorem

In this paper, we employ contour integration and residue calculus to derive explicit parity formulas for (cyclotomic) multiple zeta values (MZVs). A key innovation lies in applying double shuffle regularization to the contour integrals, which leads to two distinct regularized parity formulas-one via shuffle and one via stuffle regularization. Notably, this demonstrates for the first time that the contour integral method can be extended to the regularized setting (including the case $k_r=1$), thereby overcoming a limitation of previous approaches. Our results not only provide explicit parity relations at arbitrary depths but also lay the groundwork for extending this technique to other variants of multiple zeta values.

2601.05024Jan 2026

View

2601.04972

New gap principle for semiabelian varieties using globally valued fields

Hrushovski observed that the new gap principle of Gao-Ge-Kühne is essentially equivalent to the Bogomolov conjecture over arbitrary globally valued fields of characteristic $0$. Building on this observation, we prove a new gap principle for semiabelian varieties by reducing the Bogomolov conjecture for semiabelian varieties to the Bogomolov conjecture for abelian varieties over arbitrary GVFs. This reduction remains valid in positive characteristic; however, the corresponding Bogomolov conjecture for abelian varieties is not yet known in that setting. We prove an unconditional new gap principle in positive characteristic for semiabelian varieties whose abelian quotient is an elliptic curve.

2601.04972Jan 2026

View

2601.04743

Linear identities for partition pairs with $5$-cores

We prove an infinite family of linear identities for the number $A_5(n)$ of partition pairs of $n$ with $5$-cores by using certain theta function identities involving the Ramanujan's parameter $k(q)$ due to Cooper, and Lee and Park. Consequently, we deduce an infinite family of congruences for $A_5(n)$ using these linear identities.

2601.04743Jan 2026

View

Automorphic vector-forms using the Cohn-Elkies magic functions

In this study, we introduce the theory of what we call Hecke vector-forms. A Hecke vector-form can be viewed as a vector function representation of some quasiautomorphic form that transforms like an automorphic form on an arbitrarily chosen Hecke triangle group. In other words, because quasiautomorphic forms have complicated transformation behavior when compared with automorphic forms, the construction of a Hecke vector-form is to retrieve a transformation behavior analogous to the simpler, automorphic case. In this way, a Hecke vector-form can be viewed as the vector function analogue of an automorphic form. Since our work is for any quasi-automorphic form over an arbitrary Hecke triangle group, we briefly review the construction of such groups. Furthermore, we review the derivation of the hauptmodul, the automorphic forms, and the normalized quasiautomorphic form of weight 2 for any Hecke triangle group. We then proceed to the theory of Hecke vector-forms and establish the desired transformation behavior with respect to the generators of the associated group. A proof of this fact is strictly elementary, relying on fine properties of binomial coefficients. Lastly, we relate the vector-forms to Hecke automorphic linear differential equations, which are analogues of the frequently researched modular linear differential equations. Our results include Hecke vector-forms of the classical quasimodular forms as the simplest case.

2601.04704Jan 2026

View

2601.04503

On the average $2$-torsion in class groups and narrow class groups of cubic orders with prescribed shape

We study the distribution of $2$-torsion in class groups and narrow class groups of cubic fields and cubic orders subject to prescribed shape conditions. The \emph{shape} of a cubic order in a number field is a natural geometric invariant taking values in the modular surface $\mathbb{H}/\operatorname{GL}_2(\mathbb{Z})$. Fix a subset $W$ of the modular surface with positive hyperbolic measure and boundary of measure zero. Refining the methods of Bhargava and Varma, we prove that among cubic fields with shape in $W$, the average size of the $2$-torsion subgroup of the class group is $5/4$ for totally real fields and $3/2$ for complex fields, while the average size of the $2$-torsion subgroup of the narrow class group for totally real cubic fields is $2$. We also obtain analogous results for cubic orders satisfying prescribed local conditions at all primes.

2601.04503Jan 2026

View

2601.04437

Normal bases of small height in Galois number fields

Let $K$ be a number field of degree $d$ so that $K/\mathbb Q$ is a Galois extension. The {\it normal basis theorem} states that $K$ has a $\mathbb Q$-basis consisting of algebraic conjugates, in fact $K$ contains infinitely many such bases. We prove an effective version of this theorem, obtaining a normal basis for $K/\mathbb Q$ of bounded Weil height with an explicit bound in terms of the degree and discriminant of $K$. In the case when $d$ is prime, we obtain a particularly good bound using a different method.

2601.04437Jan 2026

View

2601.04189

Landau-Siegel zeros of Rankin-Selberg $L$-functions

We establish standard zero-free regions with no exceptional Landau-Siegel zeros for Rankin-Selberg $L$-functions and triple product $L$-functions in several new families for which modularity is not yet known.

2601.04189Jan 2026

View

2601.04014

On a conjecture of Andrews and Bachraoui

Recently, Andrews and Bachraoui considered a generating function $F_{k,m}(q)$ associated with certain two-color partitions, and conjectured that this function has non-negative coefficients for $m=1$. They showed this property for $1 \leq k \leq 4$. In this note, we prove that $F_{k,1}(q)$ has non-negative coefficients for $5 \leq k \leq 10$. Moreover, we show that, as $k\to\infty$, $F_{k,1}(q)$ is related to Ramanujan's third order mock theta function $ω(q)$ and to quotients of certain $q$-binomial coefficients.

2601.04014Jan 2026

View

2601.03998

Restricted overpartitions and concave compositions: their modularity and asymptotics

In this paper we study restricted overpartitions and concave compositions. Using q-series transformations, we show that their generating functions are related to modular forms, mock theta functions, false theta functions, and mock Maass theta functions. Moreover, we obtain their asymptotic main terms. We also study related rank statistics.

2601.03998Jan 2026

View

2601.03984

There are consecutive cubic fields with large class numbers, when ordered by discriminant

We consider cubic number fields ordered by their discriminants, and show that there exist arbitrarily long sequences that contain only fields with class numbers greater than a given bound.

2601.03984Jan 2026

View

2601.03949

Sets of distinct representations of numbers in numeral systems with a natural base and a redundant alphabet

In this work, we study a numeral system with a natural base $s \geq 2$ and a redundant alphabet $A_r=\{0,1, \dots, r\}$, where $s \leq r \leq 2s-2$. We investigate the topological, metric, and fractal properties of the set of numbers in the interval $\left[0,\frac{r}{s-1}\right]$ that admit a unique representation $x=\sum\limits_{n=1}^{\infty}\frac{α_n} {s^n}\equivΔ^{r_s}_{α_1α_2...α_n...}$, $α_n\in A_r$. The criterion for the uniqueness of the number representation is established. It is proved that the Hausdorff--Besicovitch dimension of the set of numbers with a unique representation is equal to $\frac{\ln(2s-r-1)}{\ln s}$. An analysis of the quantity of representations of numbers having purely periodic representations with a simple period (a single-digit period) is carried out. It is proved that the set of numbers that admit a continuum of distinct representations has full Lebesgue measure. Conditions for a number to belong to this set are given in terms of one of its representations.

2601.03949Jan 2026

View

2601.04284

Sobre los teoremas de Shafarevich y Siegel

Presentaremos una nueva demostración del teorema de Shafarevich sobre finitud de curvas elípticas con buena reducción fuera de un conjunto finito de primos dado. Esto da un nuevo punto de entrada a teoremas fundamentales de finitud diofantina tales como el teorema de Siegel sobre la ecuación $S$-unidad. Nuestro argumento está libre de aproximación diofantina o teoría de trascendencia, y se acerca más a las ideas de Faltings en su demostración de la conjetura de Mordell. -- We present a new proof of Shafarevich's theorem on finiteness of elliptic curves with good reduction outside a given finite set of primes. This gives a new entry point to fundamental diophantine finiteness theorems such as Siegel's theorem on the $S$-unit equation. Our proof is free from diophantine approximation or transcendence theory, and it is closer to the ideas of Faltings in his proof of Mordell's conjecture .

2601.04284Jan 2026

View

Weight filtration of Hurwitz spaces and quantum shuffle algebras

We prove an equivalence between filtrations of primitive bialgebras and filtrations of factorizable perverse sheaves, generalizing the results obtained by Kapranov-Schechtman. Under this equivalence, we find that the word length filtration of quantum shuffle algebras as defined in Ellenberg-Tran-Westerland corresponds to the codimension filtration of factorizable perverse sheaves. Furthermore, we find that the geometric weight filtration of factorizable perverse sheaves corresponds to a filtration on quantum shuffle algebras which has not been previously defined in the literature, and we call this the algebraic weight filtration. To apply this to Hurwitz spaces, we prove a comparison theorem between the weight filtrations for Hurwitz spaces over $\mathbb F_p$ and $\mathbb C$, generalizing the comparison theorem of Ellenberg-Venkatesh-Westerland. This allows us to determine the cohomological weights for Hurwitz spaces explicitly using the algebraic weight filtration of the corresponding quantum shuffle algebra. As a consequence, we find that most weights of Hurwitz spaces are smaller than expected from cohomological degree, and we prove explicit nontrivial upper bounds for weights in some cases, such as when $G=S_3$ and $c$ is the conjugacy class of transpositions.

2601.03871Jan 2026

View

2601.03797

On difference sets of dense subsets of $\mathbb{Z}^2$

In this article, we study the structure of the difference set $E - E$ for subsets $E \subseteq \mathbb{Z}^2$ of positive upper Banach density. In [Proc. Amer. Math. Soc. 146 (2018), 3449-3453, Problem 2] Fish asked whether, for every such set $E$, there exists a nonzero integer $k$ such that \[ k \cdot \mathbb{Z} \subseteq \{\, xy : (x,y) \in E - E \,\}. \] Although this question remains open, we establish a relatively weaker form of this conjecture. Specifically, we prove that there exist infinitely many integers $k \in \mathbb{Z}$ and a sequence $\langle x_n \rangle_{n \in \mathbb{N}}$ in $\mathbb{Z}$ such that \[ k \cdot FS(\langle x_n \rangle_{n \in \mathbb{N}}) \subseteq \{\, xy : (x,y) \in E - E \,\}, \] where $FS(\langle x_n \rangle)$ denotes the finite sums set generated by the sequence.

2601.03797Jan 2026

View

2601.03653

Rank metric codes from Drinfeld modules

We establish a connection between Drinfeld modules and rank metric codes, focusing on the case of semifield codes. Our framework constructs rank metric codes from linear subspaces of endomorphisms of a Drinfeld module, using tools such as characteristic polynomials on Tate modules and the Chebotarev density theorem. We show that Sheekey's construction [She20] fits naturally into this setting, yielding a short conceptual proof of one of his main results. We then give a new construction of infinite families of semifield codes arising from Drinfeld modules defined over finite fields.

2601.03653Jan 2026

View

2601.03560

The Waring Problem of Harmonic Polynomials

This paper investigates the Waring problem of harmonic polynomials. By characterizing the annihilating ideal of a homogeneous harmonic polynomial, i.e., a real binary form that is in the kernel of the Laplacian, we show that its Waring rank equals its degree. Moreover, we show that any linear form can appear in a minimal Waring decomposition of a homogeneous harmonic polynomial, implying that the forbidden locus is empty. We also provide an explicit algorithm for computing the minimal Waring decompositions.

2601.03560Jan 2026

View

Improving bounds for value sets of polynomials over finite fields

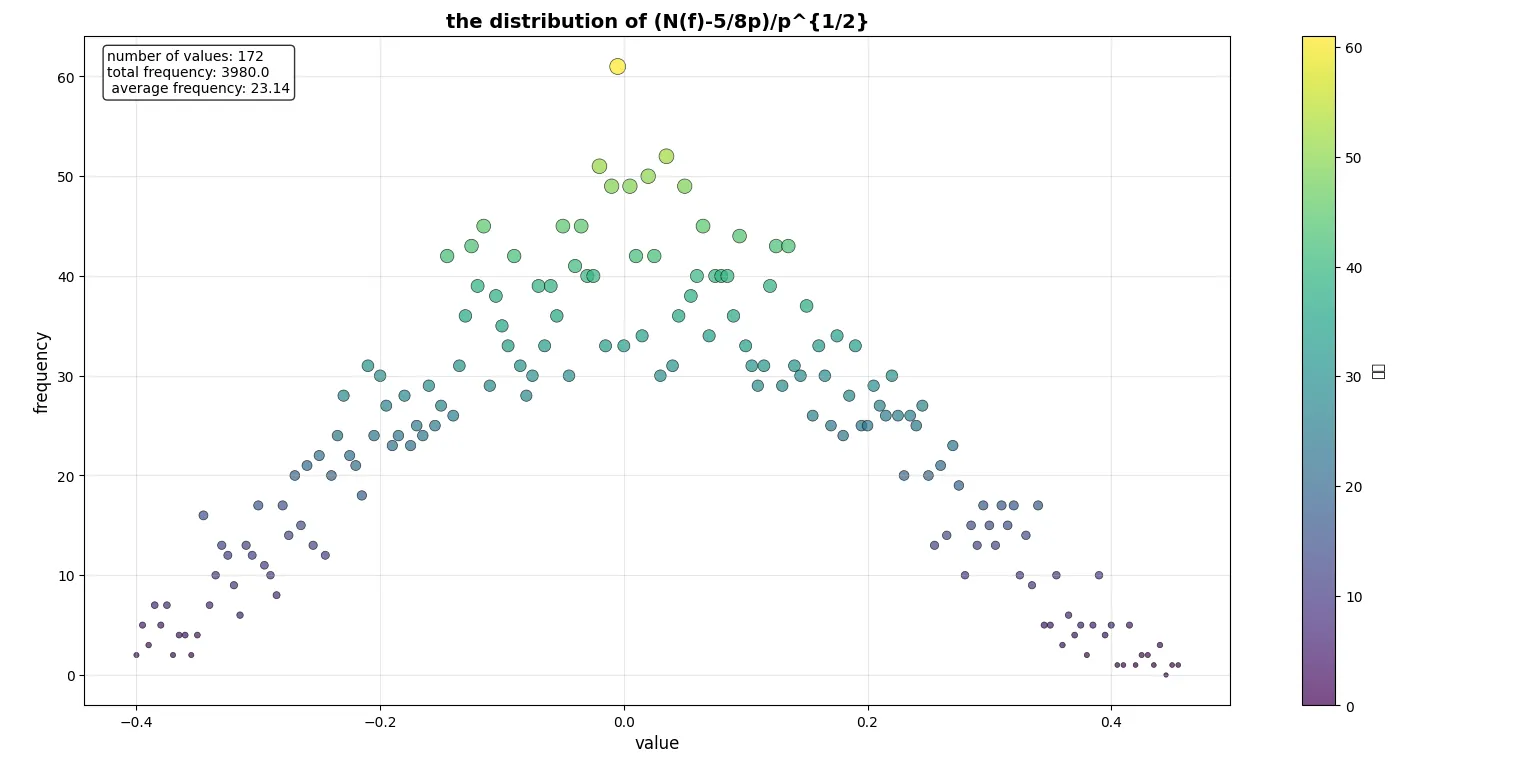
Let $\mathbb{F}_{q}$ be a finite field of characteristic $p$, and let $f \in \mathbb{F}_{q}[x]$ be a polynomial of degree $d > 0$. Denote the image set of this polynomial as $V_{f}=\{f(α)\midα\in\mathbb{F}_{q}\}$ and denote the cardinality of this set as $N_{f}$. A much sharper bound for $N_{f}$ is established in this paper. In particular, for any $p\neq 2, 3$, and for nearly every generic quartic polynomial $f \in \mathbb{F}_{q}[x]$, we obtain $$\lvert N_f - \frac{5}{8} q \rvert \leq \frac{1}{2}\sqrt{q} + \frac{3}{4},$$ which holds as a simple corollary of the main result.

2601.03548Jan 2026

View

Page 1 of 70