Numerical Analysis

Numerical methods, scientific computing, and computational mathematics

Trending in Numerical Analysis

2512.11737

A Fully Discrete Surface Finite Element Method for the Navier--Stokes equations on Evolving Surfaces with prescribed Normal Velocity

We analyze two fully time-discrete numerical schemes for the incompressible Navier-Stokes equations posed on evolving surfaces in $\mathbb{R}^3$ with prescribed normal velocity using the evolving surface finite element method (ESFEM). We employ generalized Taylor-Hood finite elements $\mathrm{\mathbf{P}}_{k_u}$-- $\mathrm{P}_{k_{pr}}$-- $\mathrm{P}_{k_λ}$, $k_u=k_{pr}+1 \geq 2$, $k_λ\geq 1$, for the spatial discretization, where the normal velocity constraint is enforced weakly via a Lagrange multiplier $λ$, and a backward Euler discretization for the time-stepping procedure. Depending on the approximation order of $λ$ and weak formulation of the Navier-Stokes equations, we present stability and error analysis for two different discrete schemes, whose difference lies in the geometric information needed. We establish optimal velocity $L^{2}_{a_h}$-norm error bounds ($a_h$ an energy norm) for both schemes when $k_λ=k_u$, but only for the more information intensive one when $k_λ=k_u-1$, using iso-parametric and super-parametric discretizations, respectively, with the help of a newly derived surface Ritz-Stokes projection. Similarly, stability and optimal convergence for the pressures is established in an $L^2_{L^2}\times L^2_{H_h^{-1}}$-norm ($H_h^{-1}$ a discrete dual space) when $k_λ=k_u$, using a novel Leray time-projection to ensure weakly divergence conformity for our discrete velocity solution at two different time-steps (surfaces). Assuming further regularity conditions for the more information intensive scheme, along with an almost weak divergence conformity result at two different time-steps, we establish optimal $L^2_{L^2}\times L^2_{L^2}$-norm pressure error bounds when $k_λ=k_u-1$, using super-parametric approximation. Simulations verifying our results are provided, along with a comparison test against a penalty approach.

2512.11737

Dec 2025Numerical Analysis

Basis Choices for Frequency Domain Statistical Independence Tests and Algorithms for Algebraic Relation Extraction

In this paper, we explore how different selections of basis functions impact the efficacy of frequency domain techniques in statistical independence tests, and study different algorithms for extracting low-dimensional algebraic relations from dependent data. We examine a range of complete orthonormal bases functions including the Legendre polynomials, Fourier series, Walsh functions, and standard and nonstandard Haar wavelet bases. We utilize fast transformation algorithms to efficiently transform physical domain data to frequency domain coefficients. The main focuses of this paper are the effectiveness of different basis selections in detecting data dependency using frequency domain data, e.g., whether varying basis choices significantly influence statistical power loss for small data with large noise; and on the stability of different optimization formulations for finding proper algebraic relations when data are dependent. We present numerical results to demonstrate the effectiveness of frequency domain-based statistical analysis methods and provide guidance for selecting the proper basis and algorithm to detect a particular type of relations.

2512.01963

Dec 2025Numerical Analysis

1,784 papers

Variable Projection Methods for Solving Regularized Separable Inverse Problems with Applications to Semi-Blind Image Deblurring

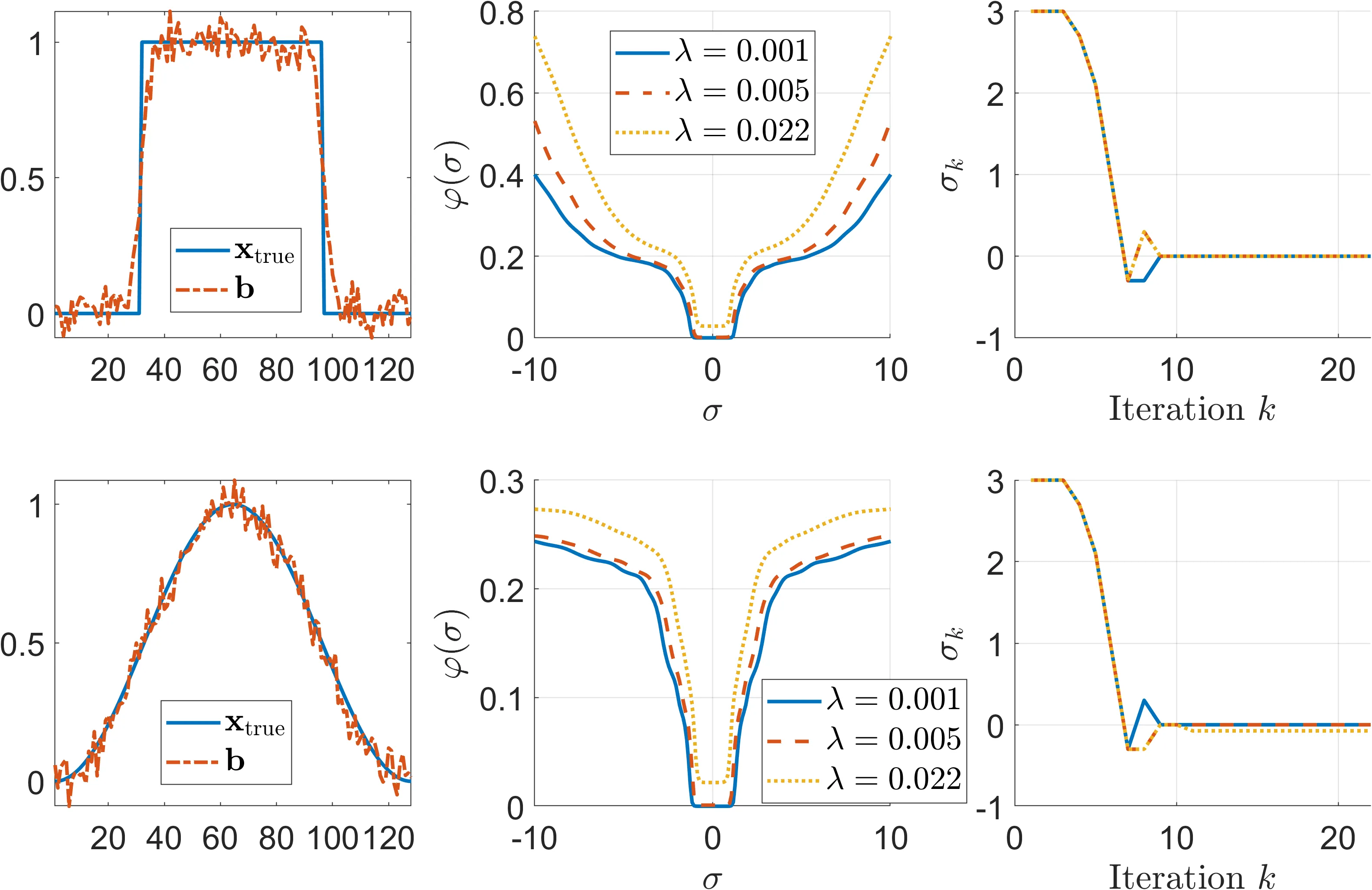
Separable nonlinear least squares problems appear in many inverse problems, including semi-blind image deblurring. The variable projection (VarPro) method provides an efficient approach for solving such problems by eliminating linear variables and reducing the problem to a smaller, nonlinear one. In this work, we extend VarPro to solve minimization problems containing a differentiable regularization term on the nonlinear parameters, along with a general-form Tikhonov regularization term on the linear variables. Furthermore, we develop a quasi-Newton method for solving the resulting reduced problem, and provide a local convergence analysis under standard smoothness assumptions, establishing conditions for superlinear or quadratic convergence. For large-scale settings, we introduce an inexact LSQR-based variant and prove its local convergence despite inner-solve and Hessian approximations. Numerical experiments on semi-blind deblurring show that parameter regularization prevents degenerate no-blur solutions and that the proposed methods achieve accurate reconstructions, with the inexact variant offering a favorable accuracy-cost tradeoff consistent with the theory.

2601.05224Jan 2026

View

A simple rigorous integrator for semilinear parabolic PDEs

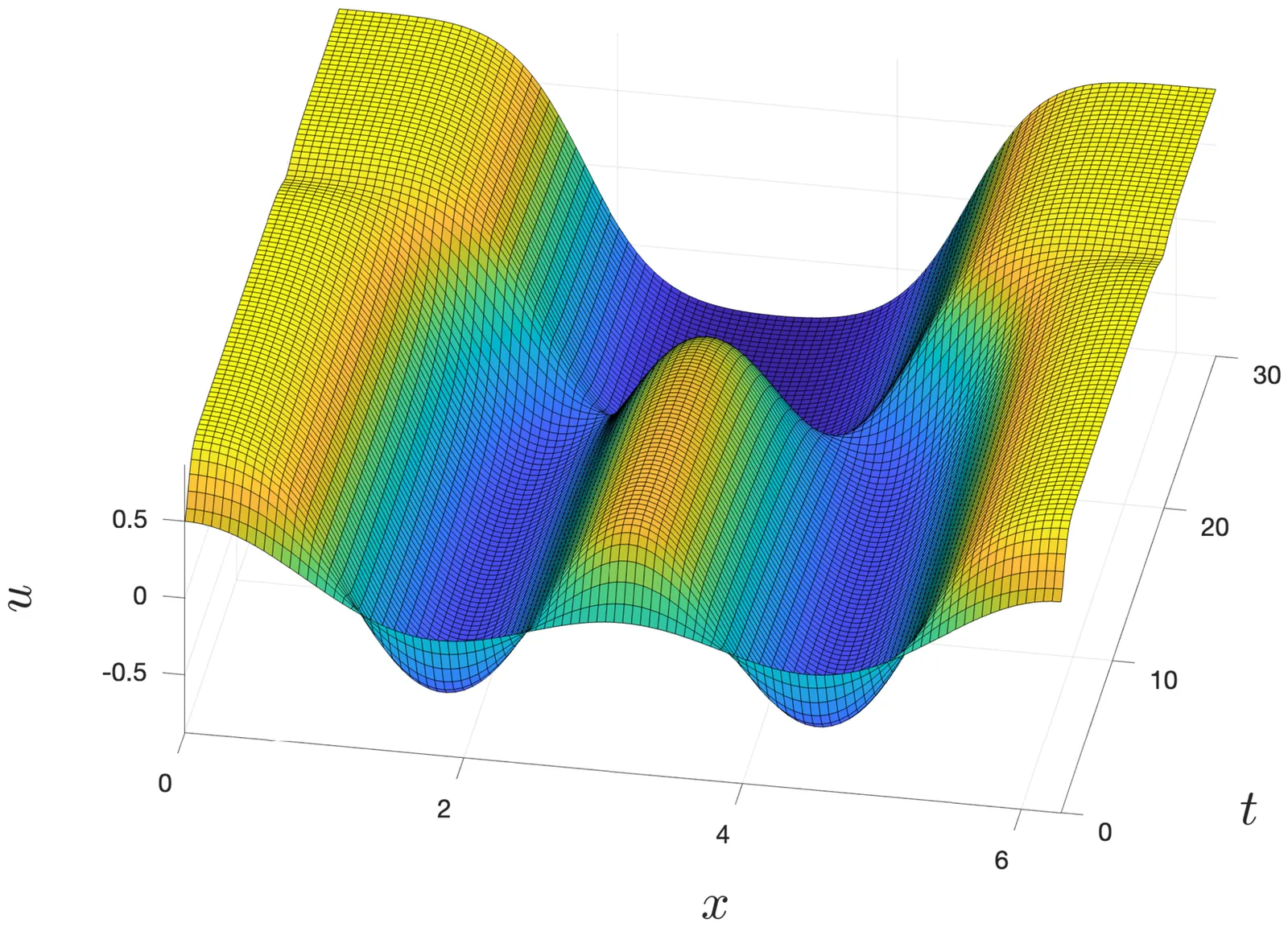
Simulations of the dynamics generated by partial differential equations (PDEs) provide approximate, numerical solutions to initial value problems. Such simulations are ubiquitous in scientific computing, but the correctness of the results is usually not guaranteed. We propose a new method for the rigorous integration of parabolic PDEs, i.e., the derivation of rigorous and explicit error bounds between the numerically obtained approximate solution and the exact one, which is then proven to exist over the entire time interval considered. These guaranteed error bounds are obtained a posteriori, using a fixed point reformulation based on a piece-wise in time constant approximation of the linearization around the numerical solution. Our setup leads to relatively simple-to-understand estimates, which has several advantages. Most critically, it allows us to optimize various aspects of the proof, and in particular to provide an adaptive time-stepping strategy. In case the solution converges to a stable hyperbolic equilibrium, we are also able to prove this convergence, applying our rigorous integrator with a final, infinitely long timestep. We showcase the ability of our method to rigorously integrate over relatively long time intervals, and to capture non-trivial dynamics, via examples on the Swift--Hohenberg equation, the Ohta--Kawasaki equation and the Kuramoto--Sivashinsky equation. We expect that the simplicity and efficiency of the approach will enable generalization to a wide variety of other parabolic PDEs, as well as applications to boundary value problems.

2601.05146Jan 2026

View

Guided Variational Network for Image Decomposition

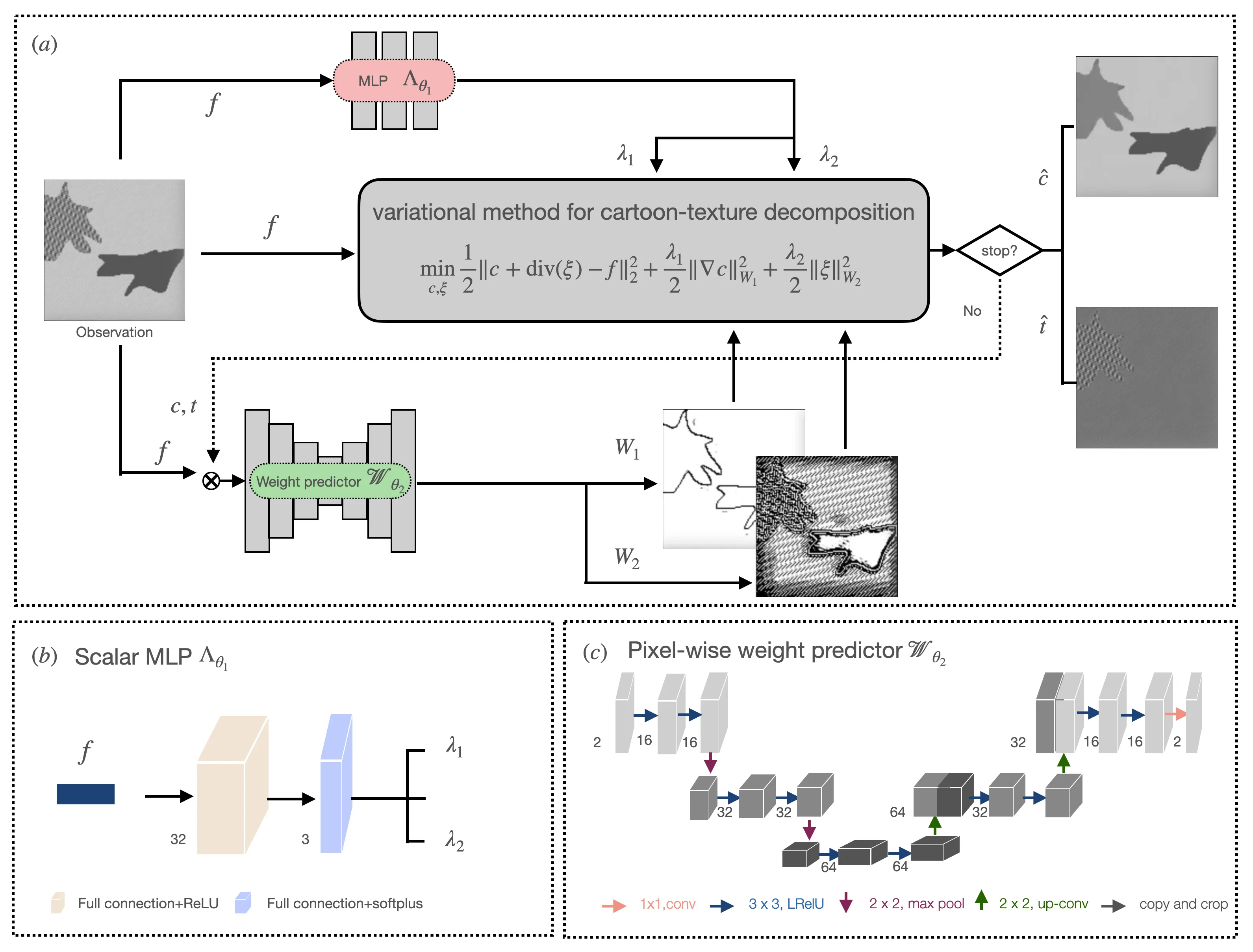
Cartoon-texture image decomposition is a critical preprocessing problem bottlenecked by the numerical intractability of classical variational or optimization models and the tedious manual tuning of global regularization parameters.We propose a Guided Variational Decomposition (GVD) model which introduces spatially adaptive quadratic norms whose pixel-wise weights are learned either through local probabilistic statistics or via a lightweight neural network within a bilevel framework.This leads to a unified, interpretable, and computationally efficient model that bridges classical variational ideas with modern adaptive and data-driven methodologies. Numerical experiments on this framework, which inherently includes automatic parameter selection, delivers GVD as a robust, self-tuning, and superior solution for reliable image decomposition.

2601.04999Jan 2026

View

Virtual Element methods for non-Newtonian shear-thickening fluid flow problems

In this work, we present a comprehensive theoretical analysis for Virtual Element discretizations of incompressible non-Newtonian flows governed by the Carreau-Yasuda constitutive law, in the shear-thickening regime (r > 2) including both degenerate (delta = 0) and non-degenerate (delta > 0) cases. The proposed Virtual Element method features two distinguishing advantages: the construction of an exactly divergence-free discrete velocity field and compatibility with general polygonal meshes. The analysis presented in this work extends a previous work, where only shear-thinning behavior (1 < r < 2) was considered. Indeed, the theoretical analysis of the shear-thickening setting requires several novel analytical tools, including: an inf-sup stability analysis of the discrete velocity-pressure coupling in non-Hilbertian norms, a stabilization term specifically designed to address the nonlinear structure as the exponent r > 2; and the introduction of a suitable discrete norm tailored to the underlying nonlinear constitutive relation. Numerical results demonstrate the practical performance of the proposed formulation.

2601.04866Jan 2026

View

A finite element method preserving the eigenvalue range of symmetric tensor fields

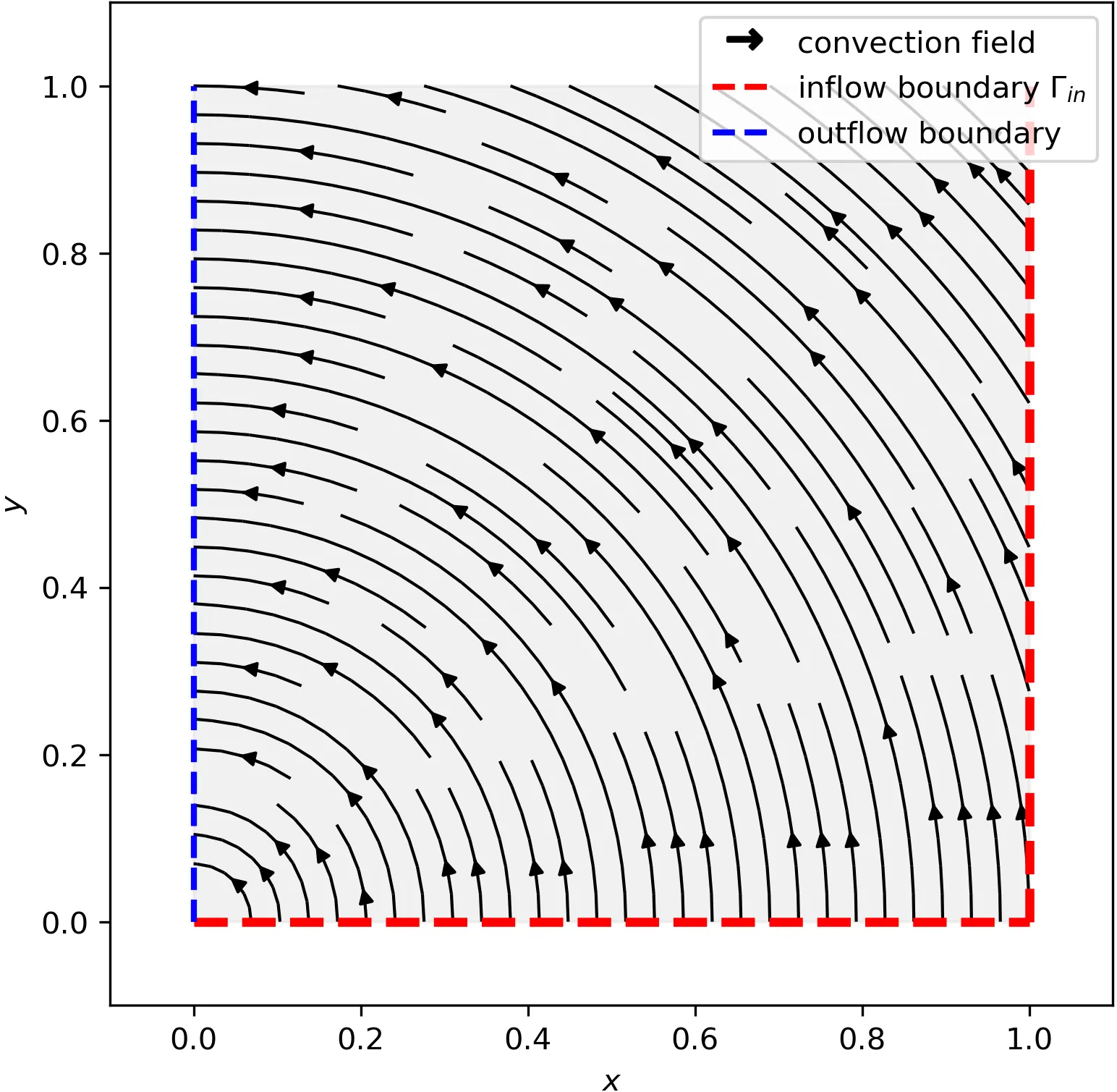
This paper presents a finite element method that preserves (at the degrees of freedom) the eigenvalue range of the solution of tensor-valued time-dependent convection--diffusion equations. Starting from a high-order spatial baseline discretisation (in this case, the CIP stabilised finite element method), our approach formulates the fully discrete problem as a variational inequality posed on a closed convex set of tensor-valued functions that respect the same eigenvalue bounds at their degrees of freedom. The numerical realisation of the scheme relies on the definition of a projection that, at each node, performs the diagonalisation of the tensor and then truncates the eigenvalues to lie within the prescribed bounds. The temporal discretisation is carried out using the implicit Euler method, and unconditional stability and optimal-order error estimates are proven for this choice. Numerical experiments confirm the theoretical findings and illustrate the method's ability to maintain eigenvalue constraints while accurately approximating solutions in the convection-dominated regime.

2601.04839Jan 2026

View

On the role of weak Marcinkiewicz-Zygmund constants in polynomial approximation by orthogonal bases

We compute numerically the $L^2$ Marcinkiewicz-Zygmund constants of cubature rules, with a special attention to their role in polynomial approximation by orthogonal bases. We test some relevant rules on domains such as the interval, the square, the disk, the triangle, the cube and the sphere. The approximation power of the corresponding least squares (LS) projection is compared with standard hyperinterpolation and its recently proposed ``exactness-relaxed'' version. The Matlab codes used for these tests are available in open-source form.

2601.04708Jan 2026

View

An HHT-$α$-based finite element framework for wave propagation in constitutively nonlinear elastic materials

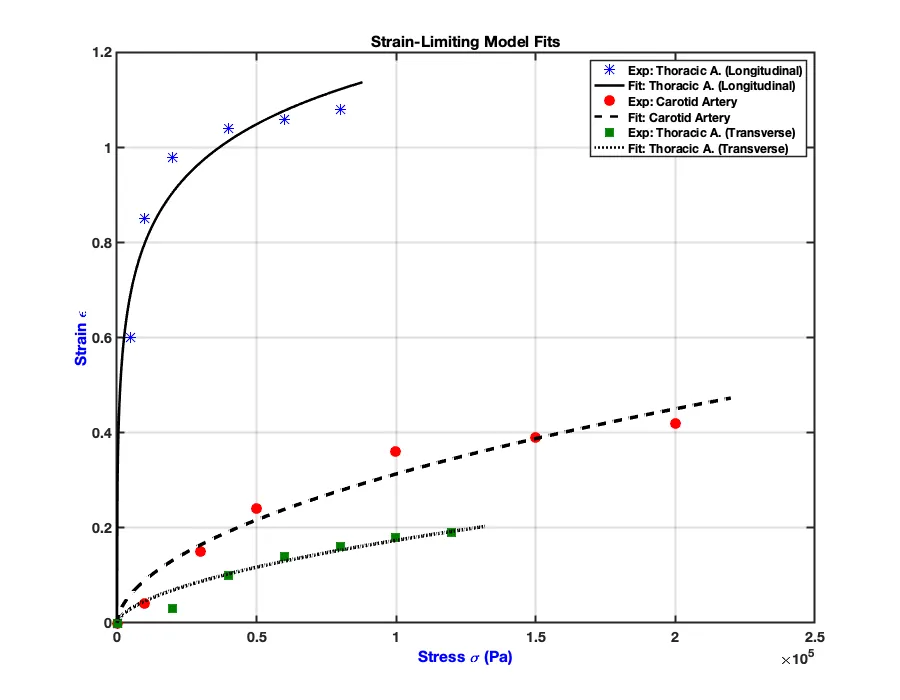
This paper presents a computational framework for modeling wave propagation in geometrically linear elastic materials characterized by algebraically nonlinear constitutive relations. We derive a specific form of the nonlinear wave equation in which the nonlinearity explicitly appears in the time-derivative terms that govern the evolution of the mechanical fields. The numerical solution is established using a fully discrete formulation that combines the standard finite element method for spatial discretization with the implicit Hilber-Hughes-Taylor (HHT)-$α$ scheme for time integration. To address the nonlinear nature of the discrete system, we employ Newton's method to iteratively solve the linearized equations at each time step. The accuracy and robustness of the proposed framework are rigorously verified through convergence analyses, which demonstrate optimal convergence rates in both space and time. Furthermore, a detailed parametric study is conducted to elucidate the influence of the model's constitutive parameters. The results reveal that the magnitude parameter of the stress-dependent variation in wave speed leads to wavefront steepening and the formation of shock discontinuities. Conversely, the exponent parameter acts as a nonlinearity filter; high values suppress nonlinear effects in small-strain regimes, whereas low values allow significant dispersive behavior. This work provides a validated tool for analyzing shock formation in advanced nonlinear materials.

2601.04628Jan 2026

View

The explicit constraint force method for optimal experimental design

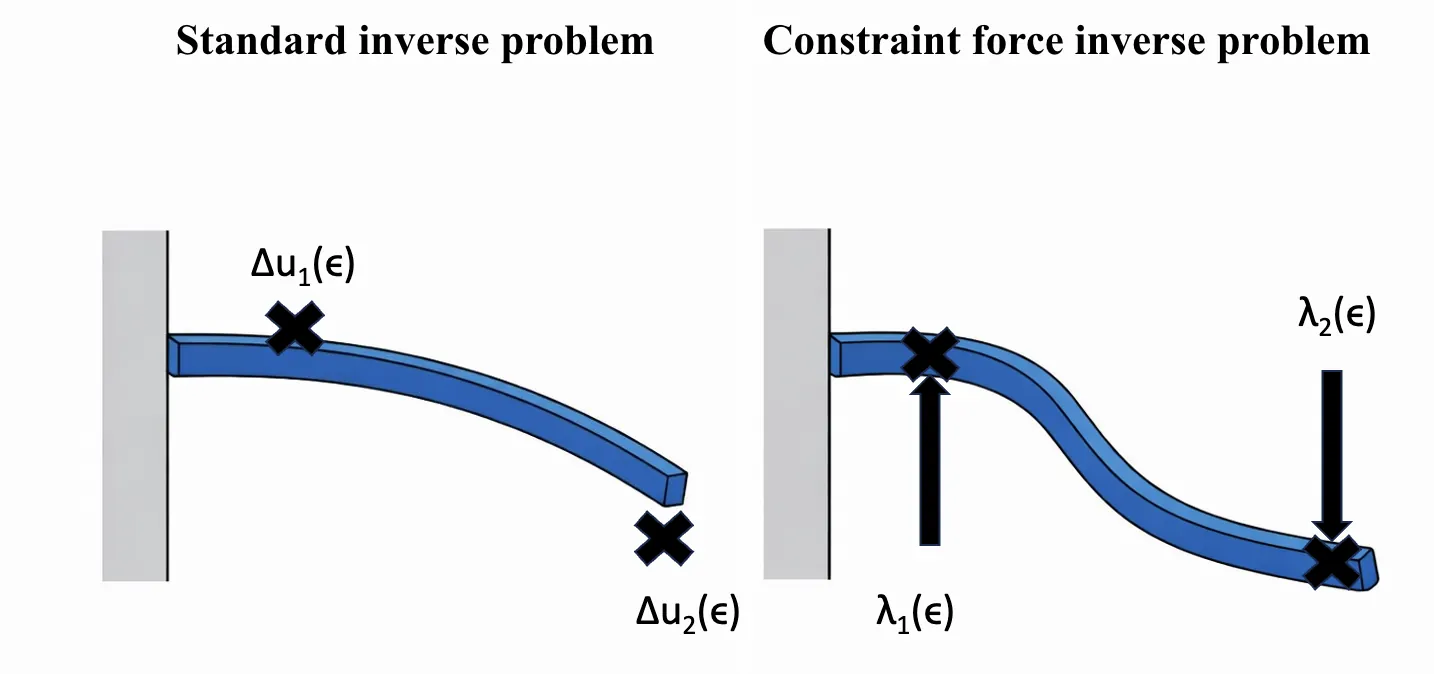
The explicit constraint force method (ECFM) was recently introduced as a novel formulation of the physics-informed solution reconstruction problem, and was subsequently extended to inverse problems. In both solution reconstruction and inverse problems, model parameters are estimated with the help of measurement data. In practice, experimentalists seek to design experiments such that the acquired data leads to the most robust recovery of the missing parameters in a subsequent inverse problem. While there are well-established techniques for designing experiments with standard approaches to the inverse problem, optimal experimental design (OED) has yet to be explored with the ECFM formulation. In this work, we investigate OED with a constraint force objective. First, we review traditional approaches to OED based on the Fisher information matrix, and propose an analogous formulation based on constraint forces. Next, we reflect on the different interpretations of the objective from standard and constraint force-based inverse problems. We then test our method on several example problems. These examples suggest that an experiment which is optimal in the sense of constraint forces tends to position measurements in the stiffest regions of the system. Because the responses -- and thus the measurements -- are small in these regions, this strategy is impractical in the presence of measurement noise and/or finite measurement precision. As such, our provisional conclusion is that ECFM is not a viable approach to OED.

2601.04557Jan 2026

View

Adaptive Multi-Grade Deep Learning for Highly Oscillatory Fredholm Integral Equations of the Second Kind

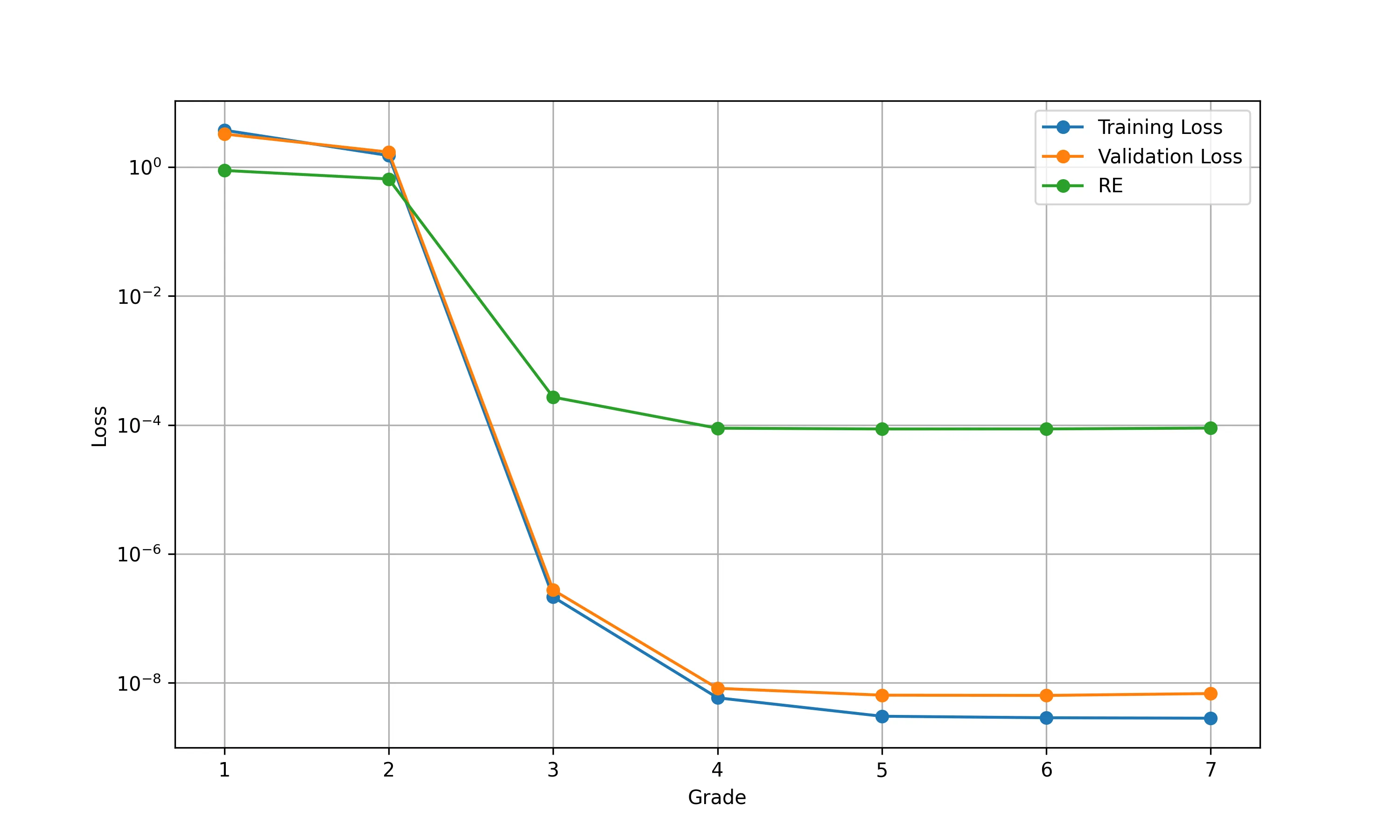
This paper studies the use of Multi-Grade Deep Learning (MGDL) for solving highly oscillatory Fredholm integral equations of the second kind. We provide rigorous error analyses of continuous and discrete MGDL models, showing that the discrete model retains the convergence and stability of its continuous counterpart under sufficiently small quadrature error. We identify the DNN training error as the primary source of approximation error, motivating a novel adaptive MGDL algorithm that selects the network grade based on training performance. Numerical experiments with highly oscillatory (including wavenumber 500) and singular solutions confirm the accuracy, effectiveness and robustness of the proposed approach.

2601.04496Jan 2026

View

Nonlinear parametrization solver for fractional Burgers equations

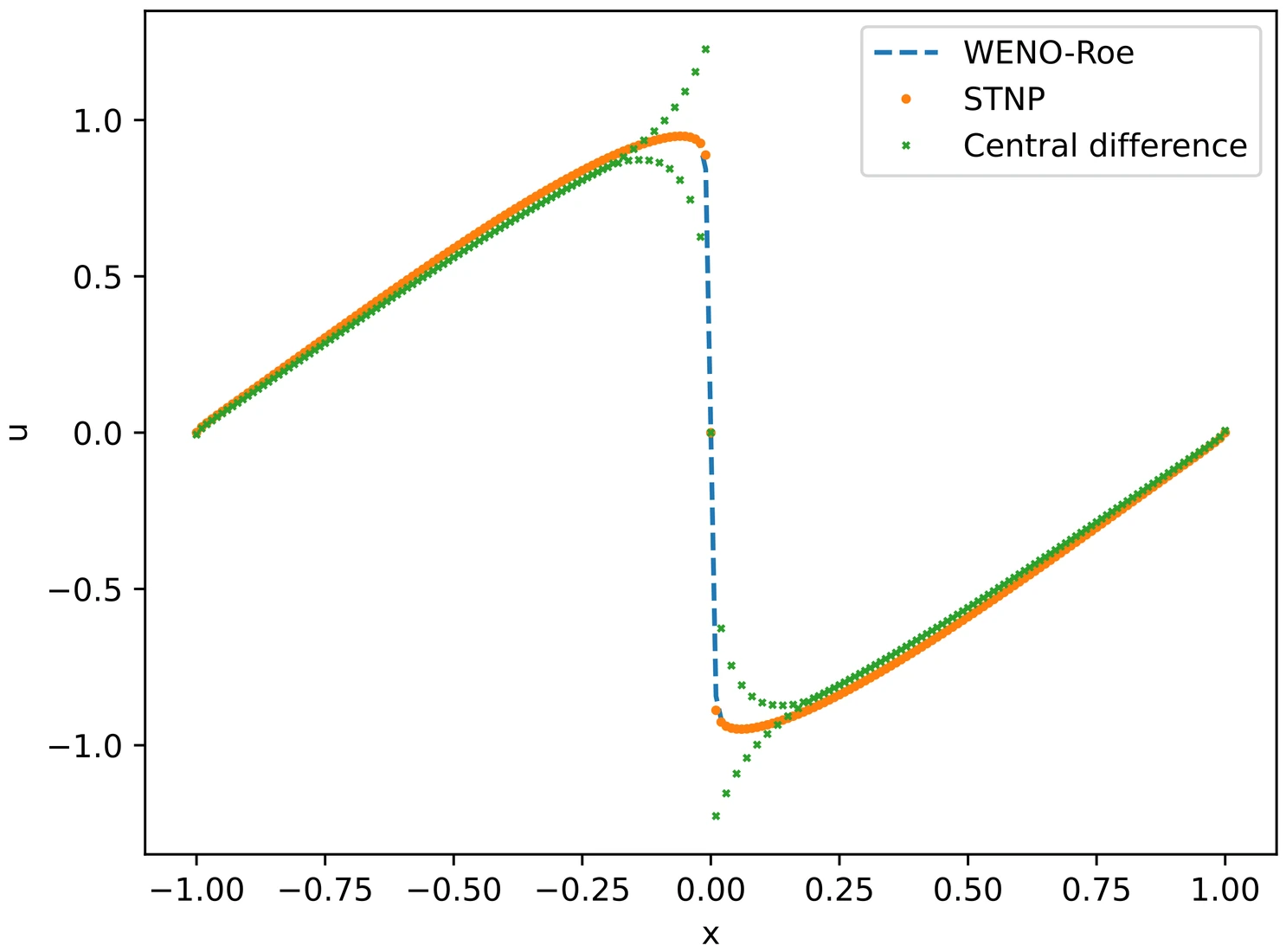
Fractional Burgers equations pose substantial challenges for classical numerical methods due to the combined effects of nonlocality and shock-forming nonlinear dynamics. In particular, linear approximation frameworks-such as spectral, finite-difference, or discontinuous Galerkin methods-often suffer from Gibbs-type oscillations or require carefully tuned stabilization mechanisms, whose effectiveness degrades in transport-dominated and long-time integration regimes. In this work, we introduce a sequential-in-time nonlinear parametrization (STNP) for solving fractional Burgers equations, including models with a fractional Laplacian or with nonlocal nonlinear fluxes. The solution is represented by a nonlinear parametric ansatz, and the parameter evolution is obtained by projecting the governing dynamics onto the tangent space of the parameter manifold through a regularized least-squares formulation at each time step. This yields a well-posed and stable time-marching scheme that preserves causality and avoids global-in-time optimization. We provide a theoretical analysis of the resulting projected dynamics, including a stability estimate and an a posteriori error bound that explicitly decomposes the total error into contributions from initial condition fitting, projection residuals, and discretization of fractional operators. Our analysis clarifies the stabilizing role of regularization and quantifies its interaction with the nonlocal discretization error. Numerical experiments for both fractional Burgers models demonstrate that STNP achieves oscillation-free shock resolution and accurately captures long-time dynamics. The method consistently outperforms high-order spectral schemes augmented with spectral vanishing viscosity, while requiring significantly fewer degrees of freedom and avoiding ad hoc stabilization.

2601.04482Jan 2026

View

2601.04479

Approximations of Extremal Eigenspace and Orthonormal Polar Factor

This paper is concerned with two extremal problems from matrix analysis. One is about approximating the top eigenspaces of a Hermitian matrix and the other one about approximating the orthonormal polar factor of a general matrix. Tight error bounds on the quality of the approximations are obtained.

2601.04479Jan 2026

View

Toward genuine efficiency and cluster robustness of preconditioned CG-like eigensolvers

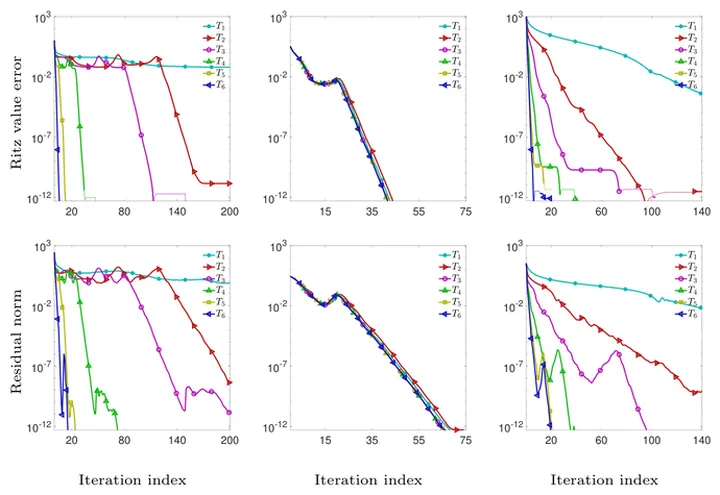
The performance of eigenvalue problem solvers (eigensolvers) depends on various factors such as preconditioning and eigenvalue distribution. Developing stable and rapidly converging vectorwise eigensolvers is a crucial step in improving the overall efficiency of their blockwise implementations. The present paper is concerned with the locally optimal block preconditioned conjugate gradient (LOBPCG) method for Hermitian eigenvalue problems, and motivated by two recently proposed alternatives for its single-vector version LOPCG. A common basis of these eigensolvers is the well-known CG method for linear systems. However, the optimality of CG search directions cannot perfectly be transferred to CG-like eigensolvers. In particular, while computing clustered eigenvalues, LOPCG and its alternatives suffer from frequent delays, leading to a staircase-shaped convergence behavior which cannot be explained by the existing estimates. Keeping this in mind, we construct a class of cluster robust vector iterations where LOPCG is replaced by asymptotically equivalent two-term recurrences and the search directions are timely corrected by selecting a far previous iterate as augmentation. The new approach significantly reduces the number of required steps and the total computational time.

2601.04429Jan 2026

View

From Penrose to Melrose: Computing Scattering Amplitudes at Infinity for Unbounded Media

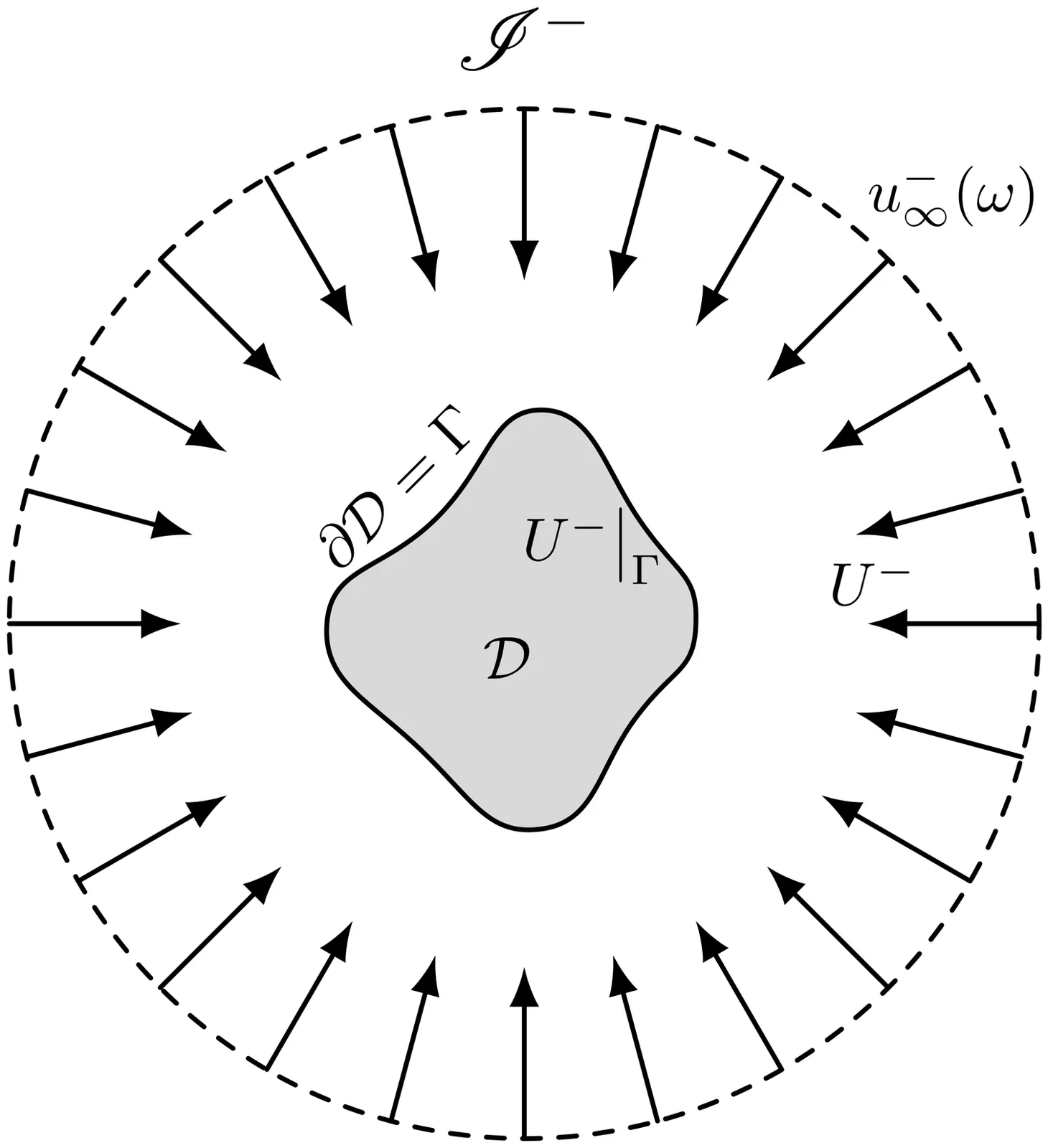
We develop a method to compute scattering amplitudes for the Helmholtz equation in variable, unbounded media with possibly long-range asymptotics. Combining Penrose's conformal compactification and Melrose's geometric scattering theory, we formulate the time-harmonic scattering problem on a compactified manifold with boundary and construct a two-step solver for scattering amplitudes at infinity. The construction is asymptotic: it treats a neighborhood of infinity, and is meant to couple to interior solvers via domain decomposition. The method provides far-field data without relying on explicit solutions or Green's function representation. Scattering in variable media is treated in a unified framework where both the incident and scattered fields solve the same background Helmholtz operator. Numerical experiments for constant, short-range, and long-range media with single-mode and Gaussian beam incidence demonstrate spectral convergence of the computed scattering amplitudes in all cases.

2601.04167Jan 2026

View

Efficient third-order iterative algorithms for computing zeros of special functions

This manuscript presents a novel and reliable third-order iterative procedure for computing the zeros of solutions to second-order ordinary differential equations. By approximating the solution of the related Riccati differential equation using the trapezoidal rule, this study has derived the proposed third-order method. This work establishes sufficient conditions to ensure the theoretical non-local convergence of the proposed method. This study provides suitable initial guesses for the proposed third-order iterative procedure to compute all zeros in a given interval of the solutions to second-order ordinary differential equations. The orthogonal polynomials like Legendre and Hermite, as well as the special functions like Bessel, Coulomb wave, confluent hypergeometric, and cylinder functions, satisfy the proposed conditions for convergence. Numerical simulations demonstrate the effectiveness of the proposed theory. This work also presents a comparative analysis with recent studies.

2601.04148Jan 2026

View

Active subspace methods and derivative-based Shapley effects for functions with non-independent variables

Lower-dimensional subspaces that impact estimates of uncertainty are often described by Linear combinations of input variables, leading to active variables. This paper extends the derivative-based active subspace methods and derivative-based Shapley effects to cope with functions with non-independent variables, and it introduces sensitivity-based active subspaces. While derivative-based subspace methods focus on directions along which the function exhibits significant variation, sensitivity-based subspace methods seek a reduced set of active variables that enables a reduction in the function's variance. We propose both theoretical results using the recent development of gradients of functions with non-independent variables and practical settings by making use of optimal computations of gradients, which admit dimension-free upper-bounds of the biases and the parametric rate of convergence. Simulations show that the relative performance of derivative-based and sensitivity-based active subspaces methods varies across different functions.

2601.04132Jan 2026

View

2601.04119

Quantitative Constraints for Stable Sampling on the Sphere

We derive quantitative volume constraints for sampling measures $μ_t$ on the unit sphere $\mathbb{S}^d$ that satisfy Marcinkiewicz-Zygmund inequalities of order $t$. Using precise localization estimates for Jacobi polynomials, we obtain explicit upper and lower bounds on the $μ_t$-mass of geodesic balls at the natural scale $t^{-1}$. Whereas constants are typically left implicit in the literature, we place special emphasis on fully explicit constants, and the results are genuinely quantitative. Moreover, these bounds yield quantitative constraints for the $s$-dimensional Hausdorff volume of Marcinkiewicz-Zygmund sampling sets and, in particular, optimal lower bounds for the length of Marcinkiewicz-Zygmund curves.

2601.04119Jan 2026

View

Algebraic Multigrid with Overlapping Schwarz Smoothers and Local Spectral Coarse Grids for Least Squares Problems

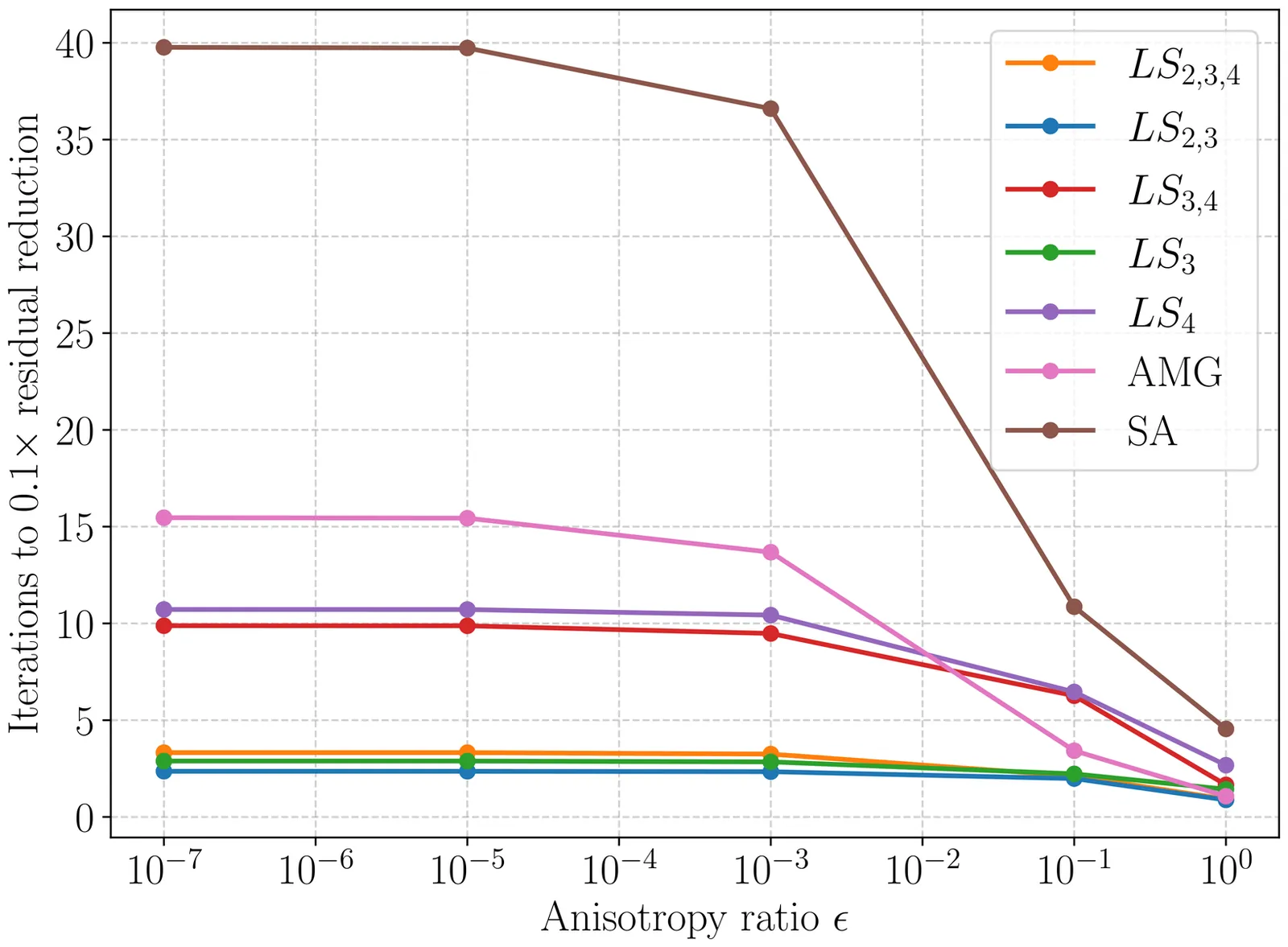
This paper develops a new algebraic multigrid (AMG) method for sparse least-squares systems of the form $A=G^TG$ motivated by challenging applications in scientific computing where classical AMG methods fail. First we review and relate the use of local spectral problems in distinct fields of literature on AMG, domain decomposition (DD), and multiscale finite elements. We then propose a new approach blending aggregation-based coarsening, overlapping Schwarz smoothers, and locally constructed spectral coarse spaces. By exploiting the factorized structure of $A$, we construct an inexpensive symmetric positive semidefinite splitting that yields local generalized eigenproblems whose solutions define sparse, nonoverlapping coarse basis functions. This enables a fully algebraic and naturally recursive multilevel hierarchy that can either coarsen slowly to achieve AMG-like operator complexities, or coarsen aggressively-with correspondingly larger local spectral problems-to ensure robustness on problems that cannot be solved by existing AMG methods. The method requires no geometric information, avoids global eigenvalue solves, and maintains efficient parallelizable setup through localized operations. Numerical experiments demonstrate that the proposed least-squares AMG-DD method achieves convergence rates independent of anisotropy on rotated diffusion problems and remains scalable with problem size, while for small amounts of anisotropy we obtain convergence and operator complexities comparable with classical AMG methods. Most notably, for extremely anisotropic heat conduction operators arising in magnetic confinement fusion, where AMG and smoothed aggregation fail to reduce the residual even marginally, our method provides robust and efficient convergence across many orders of magnitude in anisotropy strength.

2601.04112Jan 2026

View

A higher order sparse grid combination technique

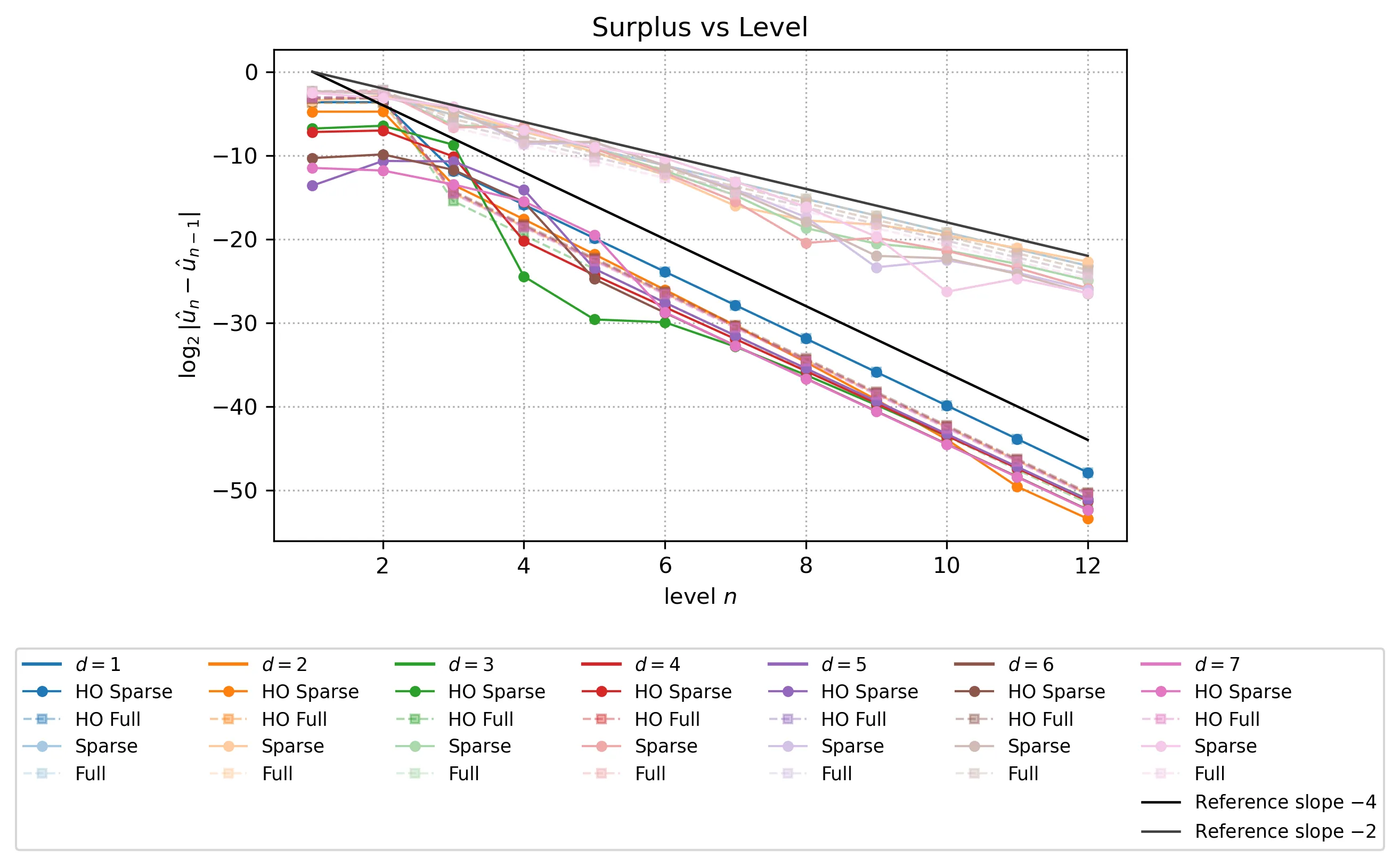
We show that a generalised sparse grid combination technique which combines multi-variate extrapolation of finite difference solutions with the standard combination formula lifts a second order accurate scheme on regular meshes to a fourth order combined sparse grid solution. In the analysis, working in a general dimension, we characterise all terms in a multivariate error expansion of the scheme as solutions of a sequence of semi-discrete problems. This is first carried out formally under suitable assumptions on the truncation error of the scheme, stability and regularity of solutions. We then verify the assumptions on the example of the Poisson problem with smooth data, and illustrate the practical convergence in up to seven dimensions.

2601.04075Jan 2026

View

A Bivariate Spline Construction of Orthonormal Polynomials over Polygonal Domains and Its Applications to Quadrature

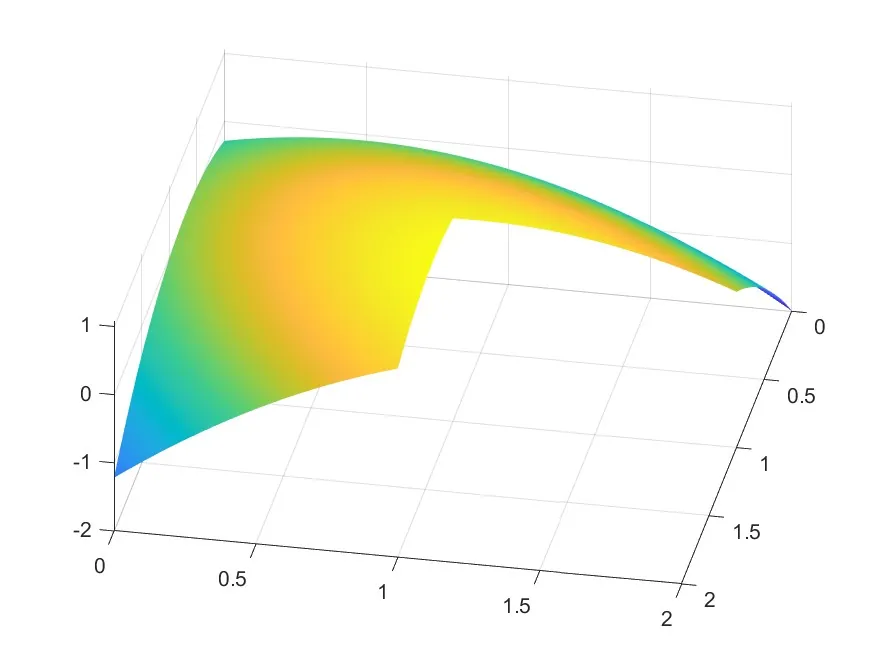
We present computational methods for constructing orthogonal/orthonormal polynomials over arbitrary polygonal domains in $\mathbb{R}^2$ using bivariate spline functions. Leveraging a mature MATLAB implementation which generates spline spaces of any degree, any smoothness over any triangulation, we have exact polynomial representation over the polygonal domain of interest. Two algorithms are developed: one constructs orthonormal polynomials of degree $d>0$ over a polygonal domain, and the other constructs orthonormal polynomials of degree $d+1$ in the orthogonal complement of $\mathbb{P}_d$. Numerical examples for degrees $d=1--5$ illustrate the structure and zero curves of these polynomials, providing evidence against the existence of Gauss quadrature on centrally symmetric domains. In addition, we introduce polynomial reduction strategies based on odd- and even-degree orthogonal polynomials, reducing the integration to the integration of its residual quadratic or linear polynomials. These reductions motivate new quadrature schemes, which we further extend through polynomial interpolation to obtain efficient, high-precision quadrature rules for various polygonal domains.

2601.04022Jan 2026

View

Posterior error bounds for prior-driven balancing in linear Gaussian inverse problems

In large-scale Bayesian inverse problems, it is often necessary to apply approximate forward models to reduce the cost of forward model evaluations, while controlling approximation quality. In the context of Bayesian inverse problems with linear forward models, Gaussian priors, and Gaussian noise, we use perturbation theory for inverses to bound the error in the approximate posterior mean and posterior covariance resulting from a linear approximate forward model. We then focus on the smoothing problem of inferring the initial condition of linear time-invariant dynamical systems, using finitely many partial state observations. For such problems, and for a specific model order reduction method based on balanced truncation, we show that the impulse response of a certain prior-driven system is closely related to the prior-preconditioned Hessian of the inverse problem. This reveals a novel connection between systems theory and inverse problems. We exploit this connection to prove the first a priori error bounds for system-theoretic model order reduction methods applied to smoothing problems. The bounds control the approximation error of the posterior mean and covariance in terms of the truncated Hankel singular values of the underlying system.

2601.03971Jan 2026

View

Page 1 of 90