Probability & Statistics
Probability theory, stochastic processes, and mathematical statistics
Probability theory, stochastic processes, and mathematical statistics
 2601.05217
2601.05217We revisit a fundamental question in hypothesis testing: given two sets of probability measures $\mathcal{P}$ and $\mathcal{Q}$, when does a nontrivial (i.e.\ strictly unbiased) test for $\mathcal{P}$ against $\mathcal{Q}$ exist? Le~Cam showed that, when $\mathcal{P}$ and $\mathcal{Q}$ have a common dominating measure, a test that has power exceeding its level by more than $\varepsilon$ exists if and only if the convex hulls of $\mathcal{P}$ and $\mathcal{Q}$ are separated in total variation distance by more than $\varepsilon$. The requirement of a dominating measure is frequently violated in nonparametric statistics. In a passing remark, Le~Cam described an approach to address more general scenarios, but he stopped short of stating a formal theorem. This work completes Le~Cam's program, by presenting a matching necessary and sufficient condition for testability: for the aforementioned theorem to hold without assumptions, one must take the closures of the convex hulls of $\mathcal{P}$ and $\mathcal{Q}$ in the space of bounded finitely additive measures. We provide simple elucidating examples, and elaborate on various subtle measure theoretic and topological points regarding compactness and achievability.
We study the non-equilibrium stationary fluctuations of a symmetric zero-range process on the discrete interval $\{1, \ldots, N-1\}$ coupled to reservoirs at sites $1$ and $N-1$, which inject and remove particles at rates proportional to $N^{-θ}$ for any value of $θ\in\mathbb{R}$. We prove that, if the jump rate is bounded and under diffusive scaling, the fluctuations converge to the solution of a generalised Ornstein-Uhlenbeck equation with characteristic operators that depend on the stationary density profile. The limiting equation is supplemented with boundary conditions of Dirichlet, Robin, or Neumann type, depending on the strength of the reservoirs. We also introduce two notions of solutions to the corresponding martingale problems, which differ according to the choice of test functions.
 2601.04974
2601.04974In this paper, we study systems of $N$ interacting particles described by the classical and relativistic Langevin dynamics with singular forces and multiplicative noises. For the classical model, we prove the ergodicity, obtaining an exponential rate of convergence to the invariant Boltzmann-Gibbs distribution, and the small-mass limit, recovering the $N$-particle interacting overdamped Langevin dynamics. For the relativistic model, we establish the ergodicity, obtaining an algebraic mixing rate of any order to the Maxwell-Jüttner distribution, and the Newtonian limit (that is when the speed of light tends to infinity), approximating a system of underdamped Langevin dynamics. The proofs rely on the construction of Lyapunov functions that account for irregular potentials and multiplicative noises.
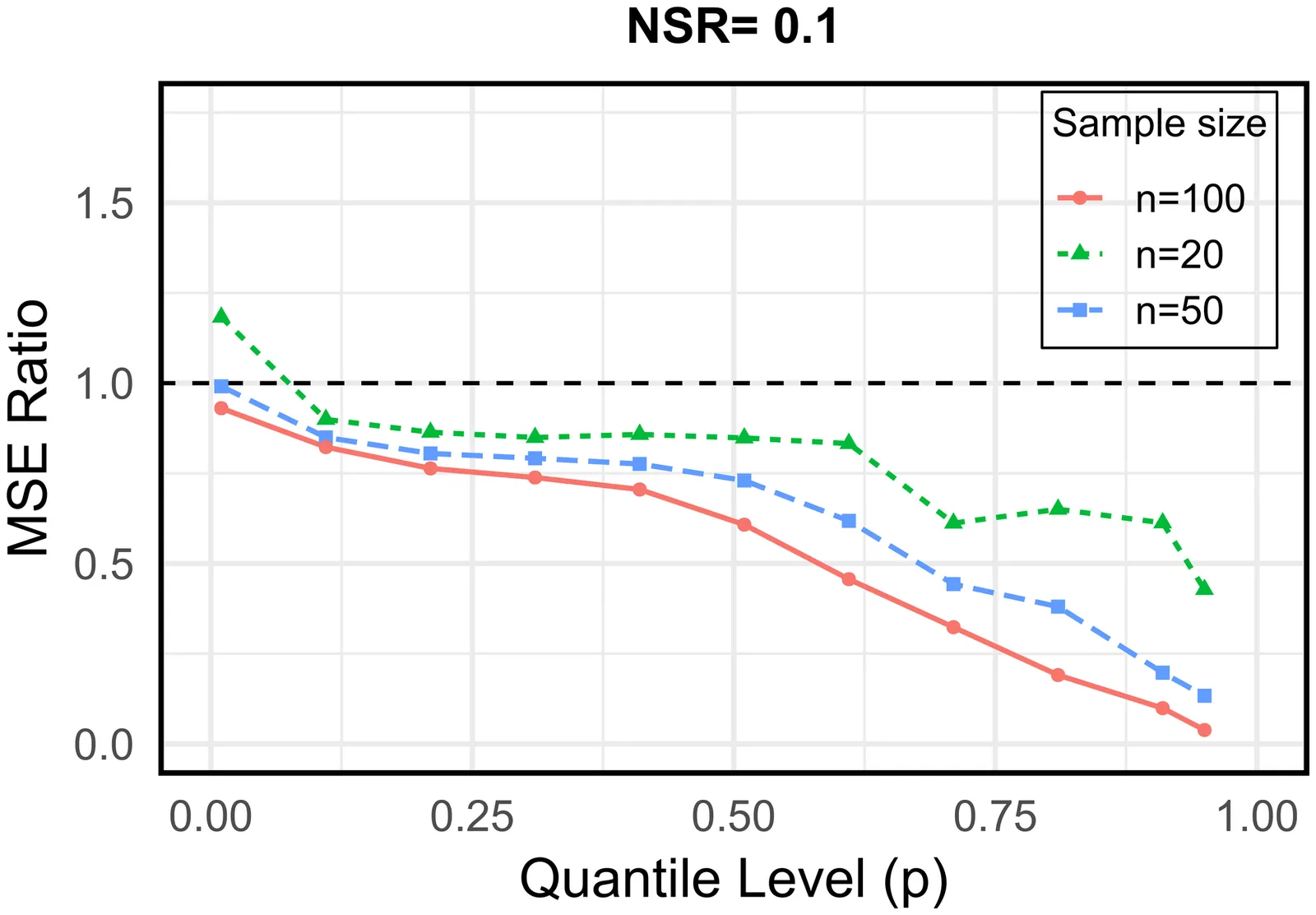
We propose an estimator of a concave cumulative distribution function under the measurement error model, where the non-negative variables of interest are perturbed by additive independent random noise. The estimator is defined as the least concave majorant on the positive half-line of the deconvolution estimator of the distribution function. We show its uniform consistency and its square root convergence in law in $\ell_\infty(\mathbb R)$. To assess the validity of the concavity assumption, we construct a test for the nonparametric null hypothesis that the distribution function is concave on the positive half-line, against the alternative that it is not. We calibrate the test using bootstrap methods. The theoretical justification for calibration led us to establish a bootstrap version of Theorem 1 in Söhl and Trabs (2012), a Donsker-type result from which we obtain, as a special case, the limiting behavior of the deconvolution estimator of the distribution function in a bootstrap setting with measurement error. Combining this Donsker-type theorem with the functional delta method, we show that the test statistic and its bootstrap version have the same limiting distribution under the null hypothesis, whereas under the alternative, the bootstrap statistic is stochastically smaller. Consequently, the power of the test tends to one, for any fixed alternative, as the sample size tends to infinity. In addition to the theoretical results for the estimator and the test, we investigate their finite-sample performance in simulation studies.
 2601.04869
2601.04869We observe that the distribution of the eigenvalues of an $N$-by-$N$ GUE random matrix is log-concave on $\mathbb{R}^N$, and that the same is true for the law of a single gap between two consecutive eigenvalues. We use this observation to prove several concentration bounds for the semicircle-renormalised eigengaps, improving on bounds recently obtained in [Tao (2024). On the distribution of eigenvalues of GUE and its minors at fixed index. [arXiv:2412.10889].
This article proposes a method for forming invariant stochastic differential systems, namely dynamic systems with trajectories belonging to a given smooth manifold. The Itô or Stratonovich stochastic differential equations with the Wiener component describe dynamic systems, and the manifold is implicitly defined by a differentiable function. A convenient implementation of the algorithm for forming invariant stochastic differential systems within symbolic computation environments characterizes the proposed method. It is based on determining a basis associated with a tangent hyperplane to the manifold. The article discusses the problem of basis degeneration and examines variants that allow for the simple construction of a basis that does not degenerate. Examples of invariant stochastic differential systems are given, and numerical simulations are performed for them.
 2601.04863
2601.04863Under reasonable algebraic assumptions and under an infinite second order moment assumption, we show that the logarithm of the norm (log-norm) of a product of random i.i.d. matrices with entries in $\mathbb{R}$ or in any other local field satisfies a generalized Central Limit Theorem (GCLT) in the sense of Paul Lévi. The proof is based on a weak law of large number for the difference $Δ_n$ between the log-norm of the product of the first $n$ matrices and the sum of their log-norms. This weak law of large numbers morally says that $Δ_n$ behaves like a sum of i.i.d. random variables that have a finite moment of order $2q$ as long as the log-norm of each matrices has a finite moment of order $q$ for a given $q > 0$. This gain of moment is the central result of the present paper and is based on the construction of pivotal times. Moreover, these results admit a nice higher rank extension when one looks at the full Cartan projection instead of the log-norm.
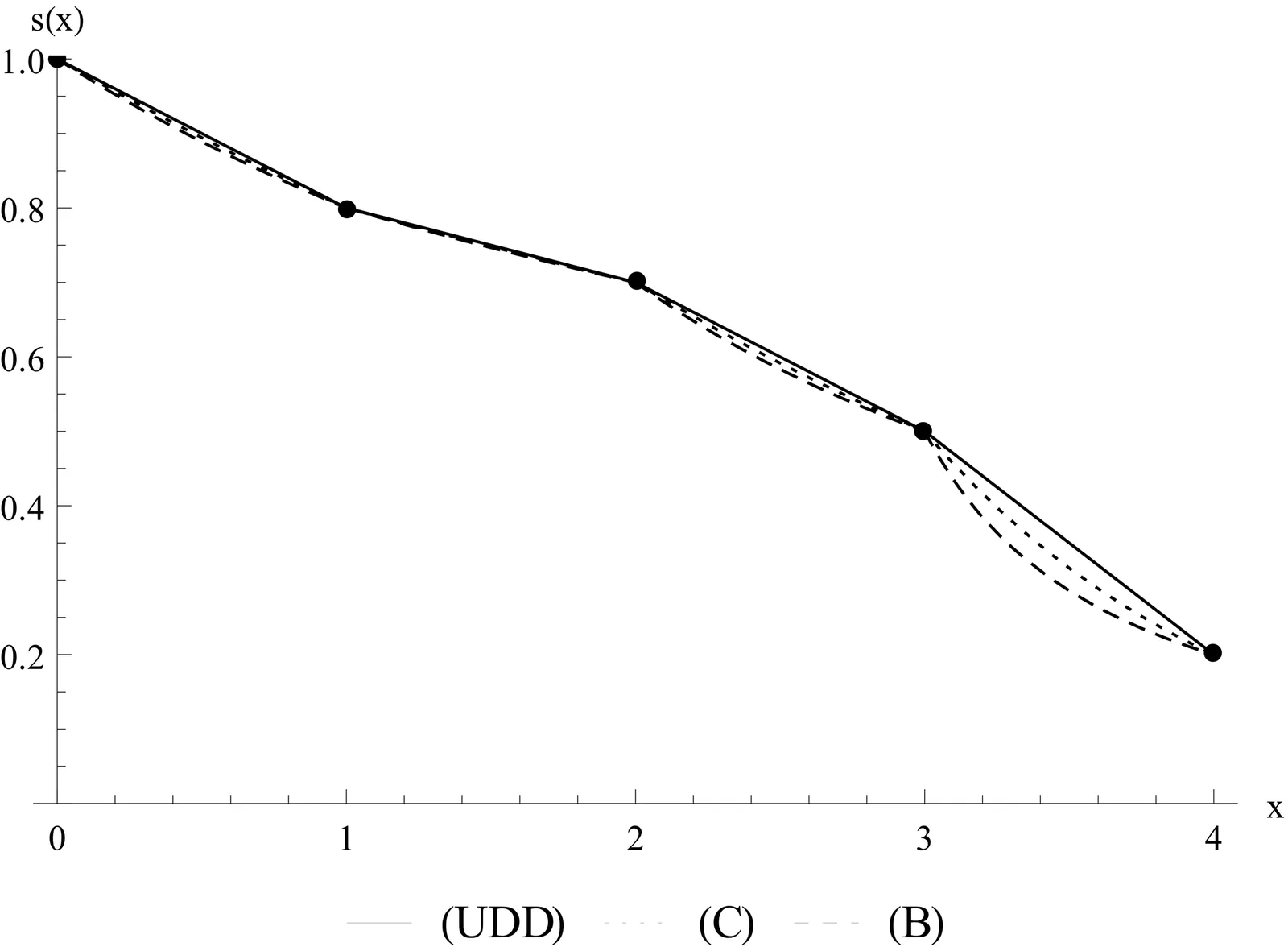
In this article, we present several formulas that make it easier to compute the net single premiums when the mortality force over the fractional ages is assumed to be constant (C). More precisely, we compute the moments of the random variables $ν^{T_x}$, $T_x$, $T_xν^{T_x}$, etc., where $T_x$ denotes the future lifetime of a person who is $x\in\{0,\,1,\,\ldots\}$ years old, and $ν$ is the annual discount multiplier. We verify the obtained formulas on the real data from the human mortality table and the Gompertz survival law. The obtained numbers are compared with the corresponding ones when the survival function over fractional ages is interpolated using the uniform distribution of deaths (UDD) and Balducci's (B) assumptions. We also formulate and prove the statement on the comparison of the moments of the mentioned random variables under assumptions (C), (UDD), and (B).
We study Brownian loop soup clusters in $\mathbb{R}^3$ for an arbitrary intensity $α>0$. We show the existence of a phase transition for the presence of unbounded clusters and study its basic properties. In particular, we show that, when $α$ is sufficiently large, almost surely all the loops are connected into a single cluster. Such a phenomenon is not observed in discrete percolation-type models. In addition, we prove the existence of a one-arm exponent and compare the clusters with the finite-range system obtained by imposing lower and upper bounds on the diameter of the loops. Finally, we provide a toolbox concerning the Brownian loop measure in $\mathbb{R}^d$, $d \ge 3$. In particular, we derive decomposition formulas by rerooting the loops in specific ways and show that the loop measure is conformally invariant, generalising results of [Lup18] in dimension 1 and [LW04] in dimension 2.
 2601.04738
2601.04738In this paper, we provide the strong rate of convergence for the Euler--Maruyama scheme for multi-dimensional stochastic differential equations with uniformly locally (unbounded) Hölder continuous drift and multiplicative noise. Our technique is based on Itô--Tanaka trick (Zvonkin transformation) for unbounded drift. Moreover, in order to apply the stochastic sewing lemma, we use the heat kernel estimate for the density function of the Euler--Maruyama scheme.
 2601.04677
2601.04677This paper studies large deviation principles and weak convergence, both at the level of finite-dimensional distributions and in functional form, for a class of continuous, isotropic, centered Gaussian random fields defined on the unit sphere. The covariance functions of these fields evolve recursively through a nonlinear map induced by an activation function, reflecting the statistical dynamics of infinitely wide random neural networks as depth increases. We consider two types of centered fields, obtained by subtracting either the value at the North Pole or the spherical average. According to the behavior of the derivative at $t=1$ of the associated covariance function, we identify three regimes: low disorder, sparse, and high disorder. In the low-disorder regime, we establish functional large deviation principles and weak convergence results. In the sparse regime, we obtain large deviation principles and weak convergence for finite-dimensional distributions, while both properties fail at the functional level sense due to the emergence of discontinuities in the covariance recursion.
 2601.04584
2601.04584We study fluctuations of individual eigenvalues of kernel matrices arising from dense graphon-based random graphs. Under minimal integrability and boundedness assumptions on the graphon, we establish distributional limits for simple, well-separated eigenvalues of the associated integral operator. We show that a sharp dichotomy governs the asymptotic behavior. In the non-degenerate regime, the properly normalized empirical eigenvalue satisfies a central limit theorem with an explicit variance, whereas in the degenerate regime, the leading fluctuations vanish and the centered eigenvalue converges to an explicit weighted chi-square limit determined by the operator spectrum. Our analysis requires no smoothness or Lipschitz-type assumptions on the graphon. While earlier work under comparable integrability conditions established operator convergence and eigenspace consistency, the present results characterize the full fluctuation behavior of individual eigenvalues, thereby extending eigenvalue fluctuation theory beyond regimes accessible through operator convergence alone.
Half-space models in the Kardar-Parisi-Zhang (KPZ) universality class exhibit rich boundary phenomena that alter the asymptotic behavior familiar from their full-space counterparts. A distinguishing feature of these systems is the presence of a boundary parameter that governs a transition between subcritical, critical, and supercritical regimes, characterized by different scaling exponents and fluctuation statistics. In this paper we construct the pinned half-space Airy line ensemble $\mathcal{A}^{\mathrm{hs}; \infty}$ on $[0,\infty)$ -- a natural half-space analogue of the Airy line ensemble -- expected to arise as the universal scaling limit of supercritical half-space KPZ models. The ensemble $\mathcal{A}^{\mathrm{hs}; \infty}$ is obtained as the weak limit of the critical half-space Airy line ensembles $\mathcal{A}^{\mathrm{hs}; \varpi}$ introduced in arXiv:2505.01798 as the boundary parameter $\varpi$ tends to infinity. We show that $\mathcal{A}^{\mathrm{hs}; \infty}$ has a Pfaffian point process structure with an explicit correlation kernel and that, after a parabolic shift, it satisfies a one-sided Brownian Gibbs property described by pairwise pinned Brownian motions. Far from the origin, $\mathcal{A}^{\mathrm{hs}; \infty}$ converges to the standard Airy line ensemble, while at the origin its distribution coincides with that of the ordered eigenvalues (with doubled multiplicity) of the stochastic Airy operator with $β= 4$.
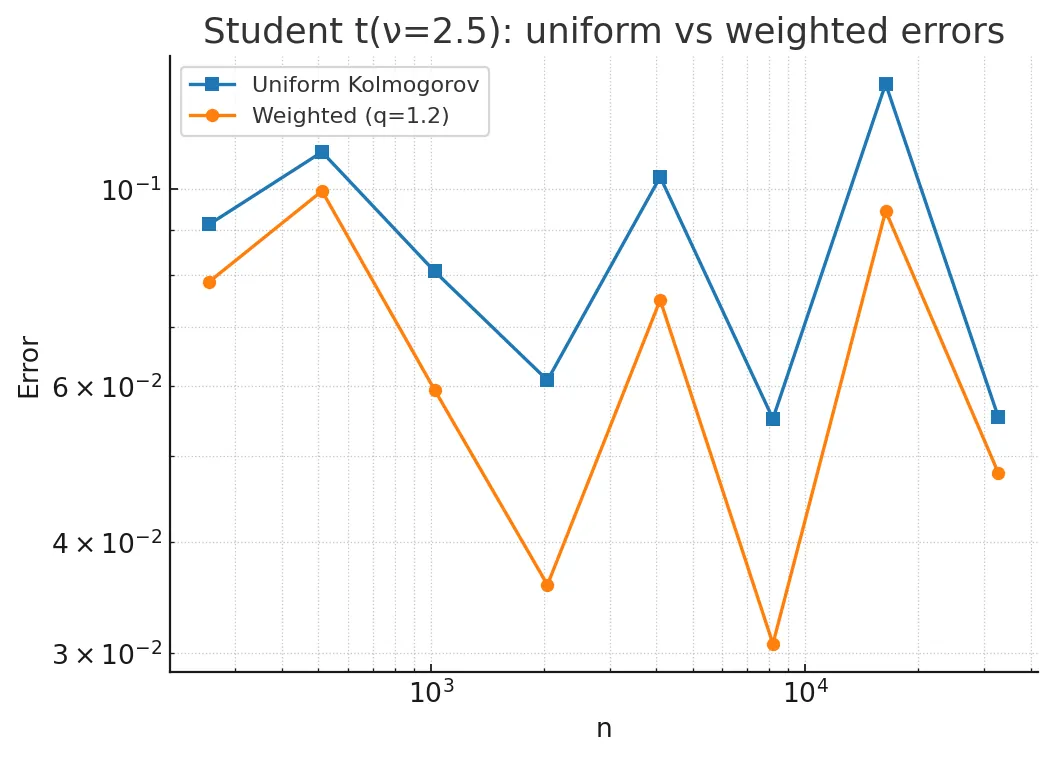
Standard risk metrics used in model validation, such as the Kolmogorov-Smirnov distance, fail to converge at practical rates when applied to high-frequency financial data characterized by heavy tails (infinite skewness). This creates a "noise barrier" where valid risk models are rejected due to tail events irrelevant to central tendency accuracy. In this paper, we introduce a Weighted Kolmogorov Metric tailored for financial time series with sub-cubic moments ($\mathbb{E}|X|^{2+δ}<\infty$). By incorporating an exhaustion function $h(x)$ that mechanically downweights extreme tail noise, we prove that we can restore the optimal Gaussian convergence rate of $O(n^{-1/2})$ even for Pareto and Student-t distributions common in Crypto and FX markets. We provide a complete proof using a core/tail truncation scheme and establish the optimal tuning of the weight parameter $q$.
This paper establishes convergence rates for learning elliptic pseudo-differential operators, a fundamental operator class in partial differential equations and mathematical physics. In a wavelet-Galerkin framework, we formulate learning over this class as a structured infinite-dimensional regression problem with multiscale sparsity. Building on this structure, we propose a sparse, data- and computation-efficient estimator, which leverages a novel matrix compression scheme tailored to the learning task and a nested-support strategy to balance approximation and estimation errors. In addition to obtaining convergence rates for the estimator, we show that the learned operator induces an efficient and stable Galerkin solver whose numerical error matches its statistical accuracy. Our results therefore contribute to bringing together operator learning, data-driven solvers, and wavelet methods in scientific computing.
 2601.04384
2601.04384Classical anti-concentration results focus on the random sum $S := \sum _{i=1}^n ξ_i v_i$, where $ξ_i$ are independent random variables and $v_i$ are real numbers. In this paper, we prove new concentration results concerning the random sum $S := \sum_{i=1}^n w_{π_i } v_i $, where $w_i , v_i$ are real numbers and $π$ is a random permutation.
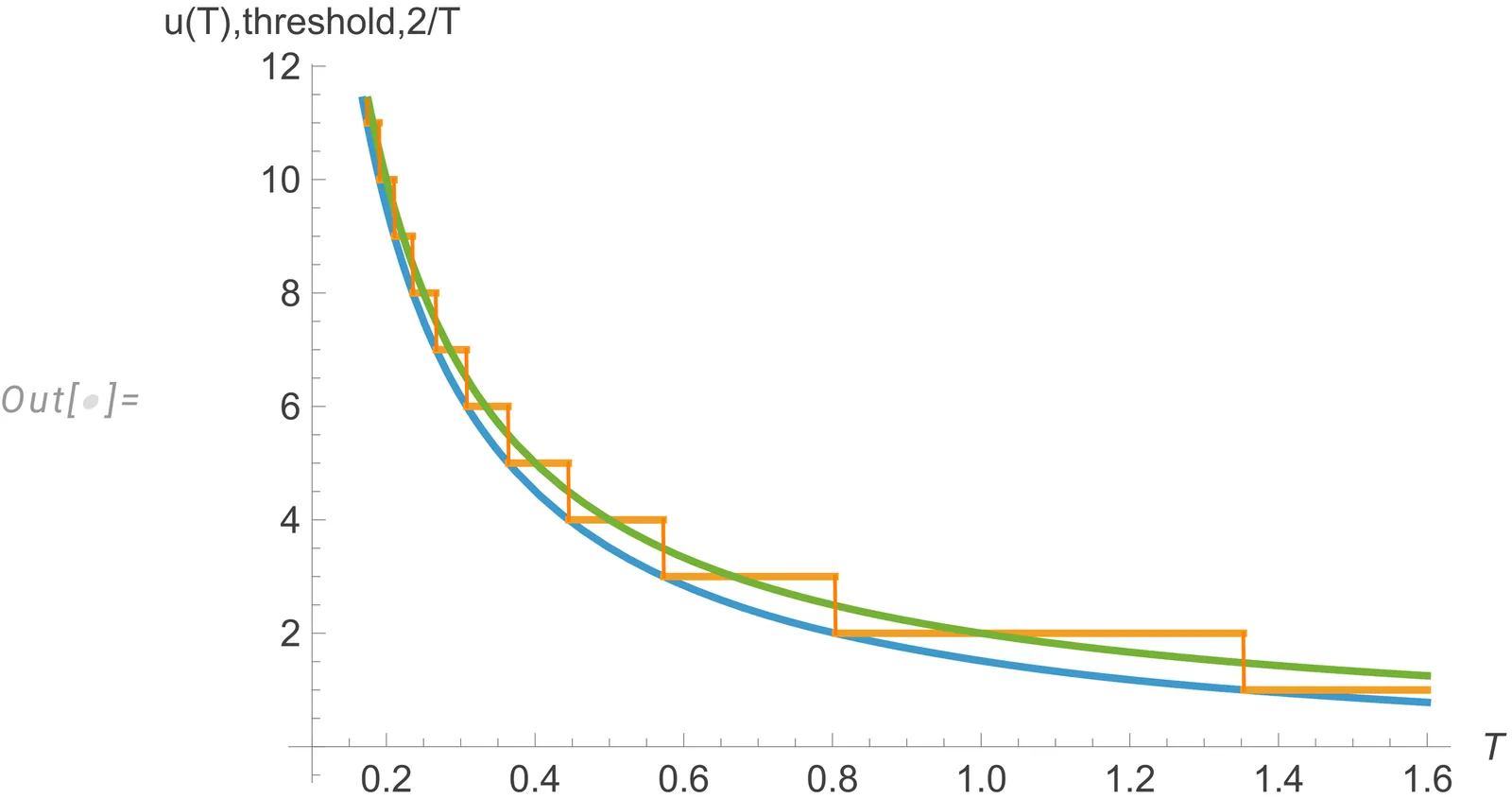
Many discrete-time optimal stopping problems are known to have more tractable limit forms based on a planar Poisson process. Using this tool we find a solution to the optimal stopping problem for i.i.d. sequence of $n$ discrete uniform random variables, in the asymptotic regime where $n$ and the range of distribution are of the same order. The optimal stopping rule in the Poisson problem is identified, by means of a time change, with known asymptotic solution to Lindley's problem of minimising the expected rank.
 2601.04161
2601.04161We study the Ergodic Properties of Random Walks in stationary ergodic environments without uniform ellipticity under a minimal assumption. There are two main components in our work. The first step is to adopt the arguments of Lawler to first prove a uniqueness principle. We use a more general definition of environments using~\textit{Environment Functions}. As a corollary, we can deduce an invariance principle under these assumptions for balanced environments under some assumptions. We also use the uniqueness principle to show that any balanced, elliptic random walk must have the same transience behaviour as the simple symmetric random walk. The second is to transfer the results we deduce in balanced environments to general ergodic environments(under some assumptions) using a control technique to derive a measure under which the \textit{local process} is stationary and ergodic. As a consequence of our results, we deduce the Law of Large Numbers for the Random Walk and an Invariance Principle under our assumptions.
 2601.04079
2601.04079We study the total variation distance under two information-erasing maps on inhomogeneous Bernoulli product measures: summation and homogenization. While summation is a Markov kernel and hence satisfies the usual data processing inequality, homogenization -- which maps each Bernoulli parameter to the cumulative mean -- is not. Nevertheless, we prove that the homogenization map also reduces the TV distance, up to a universal constant. The argument is based on an explicit two-sided control of the TV distance between Poisson binomials, obtained via a parameter interpolation and a second-moment extraction lemma.
 2601.04038
2601.04038The class of generalized gamma convolutions (GGC) is closed with respect to (wrt) change of scales, weak limits and addition and multiplication of independent random variables. Our main result adds the new property that GGC is also closed wrt q-th powers, q>1. The proof uses explicit formulas for the densities of finite sums of independent gamma variables, hyperbolically completely monotone functions (HCM) and the Laplace transform. The result is applied to sums and products of independent gamma variables and to symmetric extended GGC (symEGGC).