Algebraic Geometry
arXiv:math.AG
Algebraic varieties, stacks, sheaves, schemes, moduli spaces, complex geometry, quantum cohomology.
Looking for a broader view? This category is part of:
1,475 papers
2601.04430Maximal Variation in the Moduli of Curves
We introduce and study the maximal-variation locus in families and moduli spaces of projective curves, defined via conductor-level balancing of meromorphic differentials on the normalization. This notion captures precisely when the space of canonical differentials behaves with the expected dimension under degeneration. We prove semicontinuity and openness results showing that maximal variation is stable in flat families, identify a natural determinantal degeneracy locus where maximal variation fails, and establish that this failure is governed entirely by the presence of non-Gorenstein singularities. In particular, all smooth and nodal curves satisfy maximal variation, while every non-Gorenstein singularity contributes explicitly and additively to degeneracy. We compute the expected codimension of degeneracy loci, describe their closure and adjacency relations in moduli, and explain how non-Gorenstein defects give rise to additional Hodge-theoretic phenomena in degenerations. This framework provides a uniform, intrinsic, and deformation-theoretically meaningful classification of degeneracy in spaces of canonical differentials.
2601.04430Jan 2026
View2601.04427On automorphisms of $p$-torsion $\mathbf{G}_m$-gerbes
Olsson showed in [Ols25] that if $\mathcal{X} \to X$ is a $\mathbf{G}_m$-gerbe over a smooth projective variety over an algebraically closed field $k$ such that the Brauer class of $\mathcal{X}$ has order prime to the characteristic of $k$, then the homomorphism of $k$-group algebraic spaces $\operatorname{Aut}^0_{\mathcal{X}} \to \operatorname{Aut}^0_X$ is surjective. We provide an example to show that this need not be the case when the Brauer class of $\mathcal{X}$ has order equal to the characteristic. Our main tools are deformation theory of the fppf sheafified Artin--Mazur formal groups and nice properties of the flat cohomology of ordinary varieties in positive characteristic which are presumably well-known, but which we collect and give an exposition of here. We additionally prove some sufficient conditions for surjectivity of $\operatorname{Aut}^0_{\mathcal{X}} \to \operatorname{Aut}^0_X$ using representability results of Bragg and Olsson.
2601.04427Jan 2026
View2601.04410Infinitesimal Variations of Hodge Structure for Singular Curves I
We study the infinitesimal variation of Hodge structure associated with families of reduced algebraic curves with singularities. The analysis applies to curves beyond the nodal case and is not restricted to plane curves, encompassing curves lying on smooth projective surfaces as well as families with more general isolated singularities. Using deformation-theoretic and residue-theoretic methods, we describe how the infinitesimal period map decomposes into local contributions supported at singular points, together with global constraints arising from the geometry of the normalization. While nodal singularities give rise to nontrivial rank-one contributions, other singularities may contribute only through higher-order local data or may be invisible at the infinitesimal level. As a consequence, we obtain sharp criteria for maximal infinitesimal variation in terms of numerical invariants of the curve, notably when the number of nodes satisfies the inequality $δ\ge g$, where $g$ denotes the genus of the normalization. We extend these results to curves on very general surfaces in projective three-space, showing that maximal variation persists on Picard-rank-one surfaces but fails for sufficiently large genus in the presence of higher ADE singularities. These results extend classical maximality phenomena in infinitesimal Hodge theory to a broader singular and geometric setting.
2601.04410Jan 2026
View
Elimination Without Eliminating: Computing Complements of Real Hypersurfaces Using Pseudo-Witness Sets
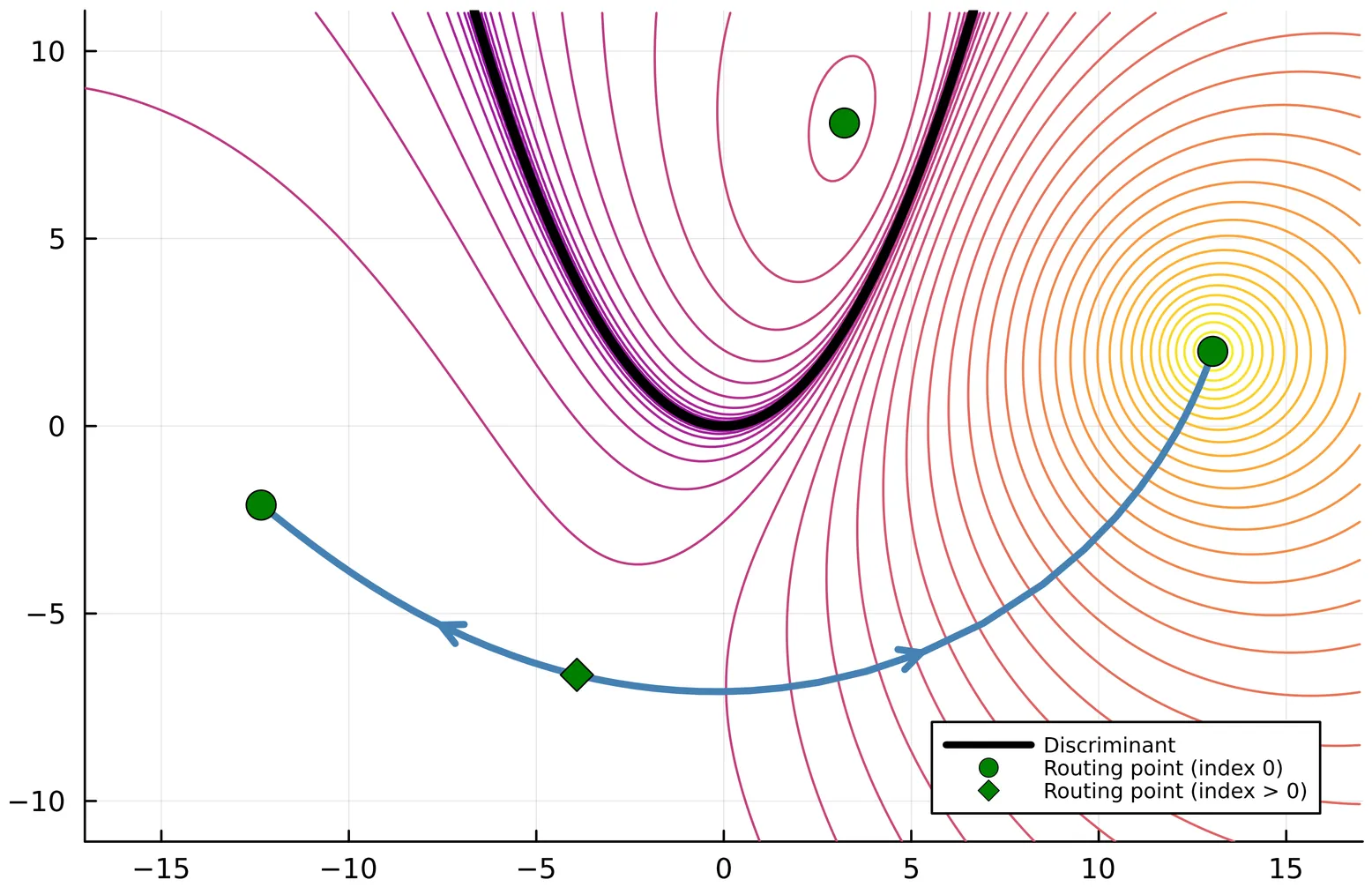
Many hypersurfaces in algebraic geometry, such as discriminants, arise as the projection of another variety. The real complement of such a hypersurface partitions its ambient space into open regions. In this paper, we propose a new method for computing these regions. Existing methods for computing regions require the explicit equation of the hypersurface as input. However, computing this equation by elimination can be computationally demanding or even infeasible. Our approach instead derives from univariate interpolation by computing the intersection of the hypersurface with a line. Such an intersection can be done using so-called pseudo-witness sets without computing a defining equation for the hypersurface - we perform elimination without actually eliminating. We implement our approach in a forthcoming Julia package and demonstrate, on several examples, that the resulting algorithm accurately recovers all regions of the real complement of a hypersurface.
2601.04383Jan 2026
View
Torelli loci, product cycles, and the homomorphism conjecture for $\mathcal{A}_g$
The tautological $\mathbb{Q}$-subalgebra $\mathsf{R}^*(\mathcal{A}_g) \subset \mathsf{CH}^*(\mathcal{A}_g)$ of the Chow ring of the moduli space of principally polarized abelian varieties is generated by the Chern classes of the Hodge bundle. There is a canonical $\mathbb{Q}$-linear projection operator $\mathsf{taut}: \mathsf{CH}^*(\mathcal{A}_g) \rightarrow \mathsf{R}^*(\mathcal{A}_g).$ We present here new calculations of intersection products of the Torelli locus in $\mathcal{A}_g$ with the product loci $\mathcal{A}_{r}\times \mathcal{A}_{g-r} \rightarrow \mathcal{A}_g$ for $r\leq 3$. The results suggest that $\mathsf{taut}$ is a $\mathbb{Q}$-algebra homomorphism, at least for special cycles. We discuss a conjectural framework for this homomorphism property. Our calculations follow two independent approaches. The first is a direct study of the excess intersection geometry of the fiber product of the Torelli and product morphisms. The second recasts the geometry in terms of families Gromov-Witten classes, which are computed by a wall-crossing formula related to unramified maps. We define tautological projections of cycles on the fiber products $\mathcal X_g^s \to \mathcal A_g$ of the universal family. We compute these projections for a class of product cycles on $\mathcal X_g^s$ in terms of a determinant involving the universal theta divisors and Poincaré classes. Using Abel-Jacobi pullbacks of product cycles on $\mathcal X_g^s$ and their projections, we construct a new family of classes which we conjecture to lie in the Gorenstein kernels of the tautological rings $\mathsf{R}^*(\mathcal M^{\mathrm{ct}}_{g,n})$. In particular, we construct a nontrivial element of the Gorenstein kernel of $\mathsf{R}^5(\mathcal{M}_{5,2}^{\mathrm{ct}})$.
2601.04353Jan 2026
View
Open $r$-spin theory in genus one, and the Gelfand-Dikii wave function
We construct the $g=1$ sector of the open $r$-spin theory, that is, an open $r$-spin theory on the moduli space of cylinders. This is the second construction of a $g>0$ open intersection theory, which includes descendents (the first is the all genus construction of the intersection theory on moduli of open Riemann surfaces with boundaries [23,30], whose $g=1$ case equals to the $r=2$ case of our construction). Unlike the construction of [30], in order to construct the $r$-spin cylinder theory we had to overcome the foundational problem of dimension jump loci, which in analogous closed theories has been treated using virtual fundamental class techniques, that are currently absent in the open setting. For this reason our construction is much more involved, and relies on the point insertion technique developed in [31,32]. We prove that the open $g=1$ potential equals, after a coordinate change, to the $g=1$ part of the Gelfand-Dikii wave function, thus confirming a conjecture of [7]. We also prove that our $g=1$ intersection numbers satisfy a $g=1$ recursion, also predicted in [7,15]. This recursion is the $g=1$ analogue of Solomon's famous $g=0$ Open WDVV equation [25], with descendents, and is also the universal $g=1$ recursion for $F$-Cohomological field theories [1]. Again, this is first geometric construction which is not the $g=1$ sector of [23,30], proven to satisfy this universal recursion.
2601.04114Jan 2026
View2601.04109Automorphisms of odd dimensional $(2,2)$-complete intersections in characteristic $2$
We compute the automorphism scheme of a generic odd dimensional $(2,2)$-complete intersection in characteristic $2$. This is the only case for complete intersections having a non-trivial identity component in automorphism schemes apart from quadric hypersurfaces and genus $1$ curves.
2601.04109Jan 2026
View2601.04064AKSZ construction for shifted Poisson structures
We prove the AKSZ theorem for shifted Poisson structures: if $X$ is an $n$-shifted Poisson derived stack, and $Y$ a $d$-oriented derived stack, then the mapping stack \[\underline{\mathrm{Map}}(Y,X)\] is naturally endowed with an $(n-d)$-shifted Poisson structure. For this, we prove that the data of an $n$-shifted Poisson structure on a derived Artin stack is equivalent to the data of an $(n+1)$-shifted Lagrangian thickening of it. We also extend the definition of shifted Poisson structures to derived prestacks having a deformation theory and give two applications, one for mapping stacks with a non-proper source and one in BV formalism.
2601.04064Jan 2026
View2601.04053Thomason condition for regular algebraic stacks
We show that any immersion into a concentrated regular Noetherian algebraic stack with quasi-finite and locally separated diagonal satisfies the Thomason condition. In particular, the derived category of quasi-coherent sheaves on such an algebraic stack is singly compactly generated. This extends results of Hall--Rydh from separated to locally separated diagonal, under additional regularity hypotheses.
2601.04053Jan 2026
View2601.03816Residue Balancing on Singular Curves
This paper investigates residue maps and their spanning properties for singular algebraic curves, with particular emphasis on three interconnected themes: the \emph{scheme--theoretic residue span}, the \emph{residue--balancing principle}, and \emph{residue balancing in the presence of arbitrary singularities}. Starting from the theory of dualizing sheaves on nodal curves, we reinterpret canonical and higher--order differentials as meromorphic objects on the normalization whose local principal parts are constrained by explicit residue conditions. A key result is the scheme--theoretic residue span theorem, which asserts that % for nodal curves of geometric genus $g$ with $δ$ nodes, when $δ\ge g$ the residue functionals at the nodes span $H^0(C,ω_C)^\vee$, so canonical differentials are completely determined by their residue data. This provides a concrete, linear description of $H^0(C,ω_C)$ and yields powerful applications to deformation theory, Severi varieties, and moduli problems. \vspace{0.1cm} We then develop the residue--balancing principle, showing that global residue conditions on each irreducible component of a singular curve are equivalent to local balancing conditions at the singular points. This equivalence clarifies the local--to--global structure of dualizing sheaves and extends naturally to $k$--differentials. Finally, we address the case of arbitrary singularities, where nodes no longer suffice to describe local geometry. Using normalization and the conductor ideal, we formulate a refined balancing principle that replaces simple residue cancellation by higher--order and conductor--level constraints. Together, these results provide a unified framework for understanding how local singular behavior governs global differentials and their deformations.
2601.03816Jan 2026
View2601.03691Surfaces of general type and sl_2-triples
The sl_2-triples play a fundamental role for the structure theory of Lie algebras, and representation theory in general. Here we investigate sl_2-triples of global vector fields on schemes X in positive characteristics p>0, and develop a general theory for actions of the corresponding height-one group scheme G=SL_2[F]. Sending a point to the Lie algebra of its stabilizer defines rational maps to various Grassmann varieties. For surfaces of general type, this yields fibrations in curves of genus g at least 2 over the projective line. Using properties of the corresponding moduli stack M_g, we prove that there are no smooth surfaces of general type with an sl_2-triple. On the other hand, employing Lefschetz pencils and Frobenius pullbacks we show that canonical surfaces of general type with such triples exist in abundance. In this connection, we classify the rational double points where the tangent sheaf is free or the evaluation pairing with Kähler differentials is surjetive, including characteristic two.
2601.03691Jan 2026
View2601.03406On the Ulrichness of twisted syzygies and dual syzygies bundles
Given a projective variety $X$ and a very ample line bundle $\mathcal{L}$ on $X$, we classify for which $X$ and $\mathcal{L}$ the twisted syzygies and twisted dual syzygies bundles are Ulrich with respect to the polarizations $\mathcal{L}^a$. We obtain some partial results when considering an arbitrary polarization $H$.
2601.03406Jan 2026
View2601.03179Deformations of the connected sum of Gorenstein algebras
We prove that the Gorenstein locus of the Hilbert scheme of points on $\mathbb A^n$ is non-reduced for $n>9$; we construct examples of non-reduced points that come from apolar algebras of the sum of general cubics. As a corollary, we get a non-reducedness result for the cactus scheme. We generalise the Białynicki-Birula decomposition to abstract deformation functors, providing a new method of studying deformation theory. Our construction gives us fractal structures on the nested Hilbert scheme.
2601.03179Jan 2026
View2601.03068Hamiltonian reductions as affine closures of cotangent bundles
For an irreducible non-singular affine $G$-variety $Y$ whose action is $2$-large, we prove that the Hamiltonian reduction $T^*Y/\!\!/\!\!/G$ is a symplectic variety with terminal singularities, isomorphic to the affine closure of $T^*Z_{\text{reg}}$ for $Z:=Y/\!/G$. As applications, we provide a short proof of G. Schwarz's theorem on the graded surjectivity of the push-forward map $\mathcal{D}(Y)^G\rightarrow \mathcal{D}(Z)$, and we establish the surjectivity of the symbol map on $Z$.
2601.03068Jan 2026
View2601.03036On the Hilbert-Chow crepant resolution conjecture
We prove the Hilbert-Chow crepant resolution conjecture in the exceptional curve classes for all projective surfaces and all genera. In particular, this confirms Ruan's cohomological Hilbert-Chow crepant resolution conjecture. The proof exploits Fulton-MacPherson compactifications, reducing the conjecture to the case of the affine plane. As an application, using previous results of the author, we also deduce the families DT/GW correspondence for threefolds $S \times C$ in classes that are zero on the first factor, yielding a wall-crossing proof of the correspondence in this case. Finally, we speculate on the relationship between Hilbert schemes and Fulton-MacPherson compactifications beyond the topics considered in this work.
2601.03036Jan 2026
View
K-stability of Fano weighted hypersurfaces via plt flags and convex geometry
We develop a framework to study the K-stability of weighted Fano hypersurfaces based on a combination of birational and convex-geometric techniques. As an application, we prove that all quasi-smooth weighted Fano hypersurfaces of index 1 with at most two weights greater than 1 are K-stable. We also construct several examples of K-unstable quasi-smooth weighted Fano hypersurfaces of low indices. To prove these results, we establish lower bounds for stability thresholds using the method of Abban-Zhuang, which reduces the problem to lower-dimensional cases. A key feature of our approach is the use of plt flags that are not necessarily admissible.
2601.02974Jan 2026
View2601.02741Stacks of p-adic shtukas and spatial kimberlites
The main purpose of this article is to show that the special Newton polygon map from the stack of p-adic shtukas to the stack of G-bundles on the Fargues--Fontaine curve is representable in diamonds and sufficiently nice for cohomological considerations (i.e. fdcs). The second purpose is to show that the $\bar{\mathbb{F}}_p$-fibers of the special Newton polygon map behave like formal schemes, and in particular, satisfy henselianity properties with respect to their reduced locus. These two goals achieved in this article are two of the crucial ingredients used in our collaboration with Hamman, Ivanov, Lourenço and Zou to construct the equivalence that compares the schematic and analytic local Langlands categories of Zhu and of Fargues--Scholze. To achieve these goals, we introduce and study spatial kimberlites, which is a better behaved variant of the theory previously developed by the author.
2601.02741Jan 2026
View2601.02719Symmetric quiver varieties and critical stable envelopes
Symmetric quiver varieties with potentials are natural generalizations of Nakajima quiver varieties, and their equivariant critical cohomologies provide more flexible settings for geometric representation theory and enumerative geometry. In this paper, we study their geometric properties and show that they behave like universally deformed Nakajima quiver varieties. Based on this, we provide a new proof of the existence of critical stable envelopes on them. Following an idea of Nakajima, we give a sheaf theoretic interpretation of critical stable envelopes by the hyperbolic restriction in the affinization of symmetric quiver varieties. The associativity of hyperbolic restrictions implies the triangle lemma of critical stable envelopes.
2601.02719Jan 2026
View2601.02592The fiber product of the Torelli map with any product $\mathcal{A}_{g_1}\times \dots \times \mathcal{A}_{g_k}\to\mathcal{A}_g$ is reduced
We prove that the fiber product of the Torelli map $t\colon \mathcal{M}^{ct}_g \to \mathcal{A}_g$ with any product $\mathcal{A}_{g_1}\times\dots\times \mathcal{A}_{g_k} \to \mathcal{A}_g$ for $g=g_1+\dots+g_k$ has a reduced scheme structure. As a consequence, letting $d=\text{codim}(t^*[\mathcal{A}_{g_1}\times\dots\times \mathcal{A}_{g_k}])$, we find that the class $t^*[\mathcal{A}_{g_1}\times\dots\times \mathcal{A}_{g_k}]\in \mathsf{CH}^{d}(\mathcal{M}^{ct}_g)$ is tautological. In particular, we obtain $t^*[\mathcal{A}_{g_1}\times\dots\times \mathcal{A}_{g_k}] = 0$ for $d > 2g-3.$
2601.02592Jan 2026
View2601.02235Hilbert scheme of smooth projective curves of unexpected dimension \& existence of a component with less than the expected number of moduli
We denote by $\mathcal{H}_{d,g,r}$ the Hilbert scheme of smooth curves of degree $d$ and genus $g$ in $\mathbb{P}^r$. Denoting by $\mathcal{M}_g$ the moduli space of smooth curves of genus $g$, let $μ: \mathcal{H}_{d,g,r}\dasharrow \mathcal{M}_g$ be the natural map sending $X\in\mathcal{H}_{d,g,r}$ to its isomorphism class $μ(X)=[X]\in\mathcal{M}_g$. It has been conjectured that a component $\mathcal{H}\subset\mathcal{H}_{d,g,r}$ has the minimal possible dimension $$\Xx(d,g,r):=3g-3+ρ(d,g,r)+\dim\operatorname{Aut}(\mathbb{P}^r)$$ \noindent if $\codim_{\mathcal{M}_g}μ(\mathcal{H})\le g-5$ provided $\Xx(d,g,r)\ge 0$, where $ρ(d,g,r):=g-(r+1)(g-d+r)$ is the Brill-Noether number. In this article, we exhibit examples against the conjecture discuss further for the study of the functorial map $μ: \\mathcal{H}{d,g,r}\dasharrow\mathcal{M}_g$ along this line. A component $\mathcal{H}\subset \mathcal{H}_{d,g,r}$ is said to have the {\it expected number of moduli} if $$\dimμ({\Hh})=\min\{3g-3, 3g-3+ρ(d,g,r)\},$$provided $3g-3+ρ(d,g,r)\ge 0$. The existence of a component with strictly less than the expected number of moduli has not been known. In this paper, we show the existence of components with less than the expected number of moduli.
2601.02235Jan 2026
ViewPage 1 of 74