Classical Analysis and ODEs
arXiv:math.CA
Special functions, orthogonal polynomials, harmonic analysis, ODEs, differential relations, calculus of variations, approximations, expansions.
Looking for a broader view? This category is part of:
413 papers
2601.04987The local Dirichlet integral and applications
We study the local Dirichlet integral of distance functions and their behavior within the harmonic Dirichlet space. We provide estimates for the local Dirichlet integral of distance functions, which allow us to study their membership in the algebra of multipliers of the Dirichlet space. We give sufficient condition for a closed subset of the unit circle to be polar and we also examine cyclicity in the harmonic Dirichlet spaces.
2601.04987Jan 2026
View2601.04893Convergence of Hermite expansions in modulation spaces
The aim of this paper is to give an elementary proof that Hermite expensions of a function $f$ in the modulation space $M^p(R)$ converges to $f$ in $M^p(R)$ when $1< p<+\infty$ and may diverge when $p = 1,\infty$. The result was previously established for $1< p<+\infty$ by Garling and Wojtaszczyk and for $p = 1,\infty$ by Lusky in an equivalent setting of Fock spaces by different methods. Higher dimesional results are also considered. In an appendix, we also establish upper bounds for the Zak transform of Hermite functions.
2601.04893Jan 2026
View2601.04783Szegő Mapping and Hermite--Padé Polynomials for Multiple Orthogonality on the Unit Circle
We investigate generalized Laurent multiple orthogonal polynomials on the unit circle satisfying simultaneous orthogonality conditions with respect to $r$ probability measures or linear functionals on the unit circle. We show that these polynomials can be characterized as solutions of a general two-point Hermite--Padé approximation problem. We derive Szegő-type recurrence relations, establish compatibility conditions for the associated recurrence coefficients, and obtain Christoffel--Darboux formulas as well as Heine-type determinantal representations. Furthermore, by extending the Szegő mapping and the Geronimus relations, we relate these Laurent multiple orthogonal polynomials to multiple orthogonal polynomials on the real line, thereby making explicit the connection between multiple orthogonality on the unit circle and on the real line.
2601.04783Jan 2026
View
Neumann series of Bessel functions for the solutions of the Sturm-Liouville equation in impedance form and related boundary value problems
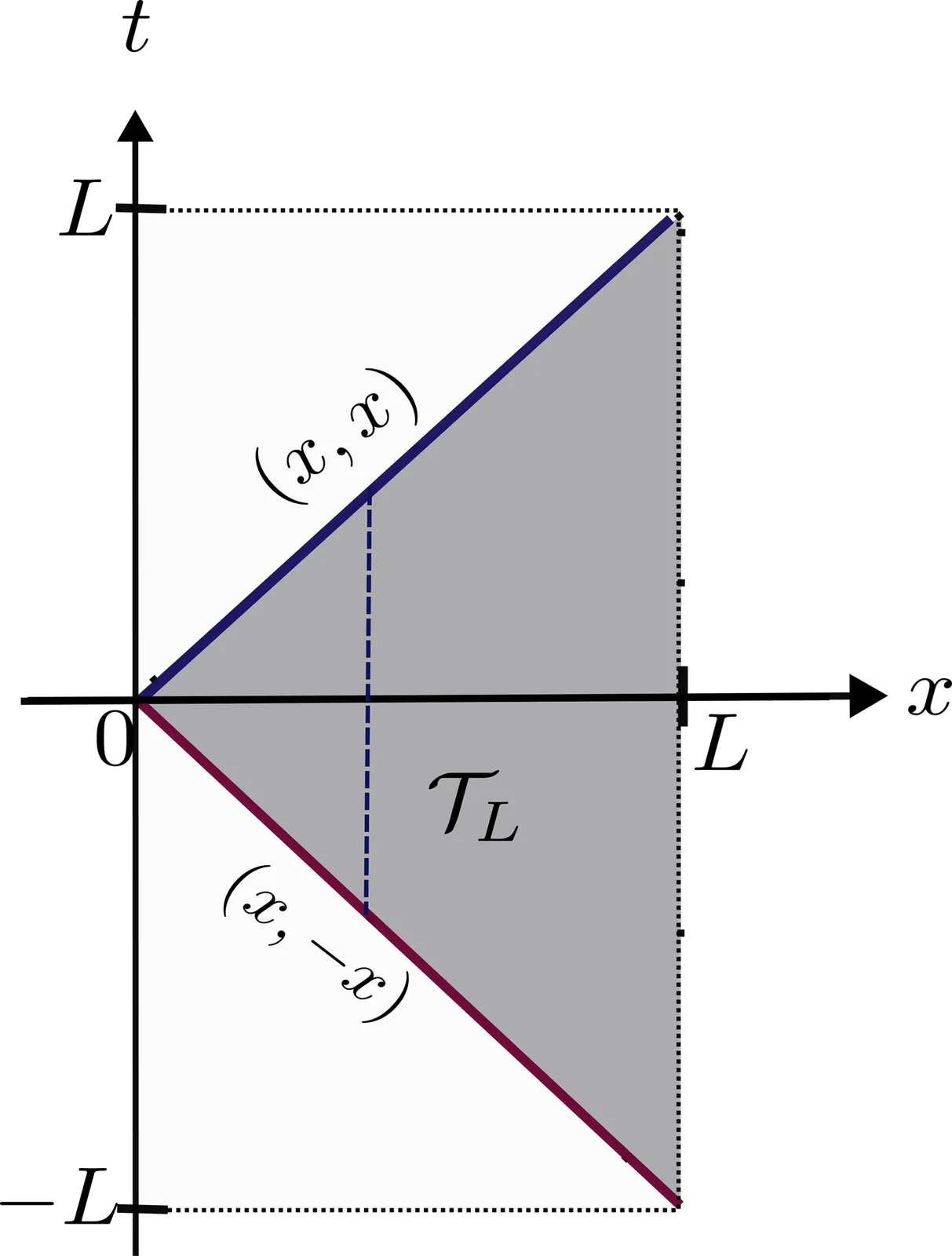
We present a Neumann series of spherical Bessel functions representation for solutions of the Sturm--Liouville equation in impedance form \[ (κ(x)u')' + λκ(x)u = 0,\quad 0 < x < L, \] in the case where $κ\in W^{1,2}(0,L)$ and has no zeros on the interval of interest. The $x$-dependent coefficients of this representation can be constructed explicitly by means of a simple recursive integration procedure. Moreover, we derive bounds for the truncation error, which are uniform whenever the spectral parameter $ρ=\sqrtλ$ satisfies a condition of the form $|\operatorname{Im}ρ|\leq C$. Based on these representations, we develop a numerical method for solving spectral problems that enables the computation of eigenvalues with non-deteriorating accuracy.
2601.04513Jan 2026
View2601.04425Five Parameter Hypergeometric 3F2(1) when One or more Parameters are Integers or Separated by Integers: Derivations, Review, Exotics and More
This work was intended to be all about, and only about, hypergeometric 3F2(1). The initial goal was to revisit many identities from the literature that have been derived over the years and show that they can be obtained in a simpler way armed, with only a minimum of elementary identities. That goal has been achieved as a (patient) reader will discover. In another sense, this work is a partial review of the last half-century's worth of progress in the evaluation of a particular set of 3F2(1), in particular those cases where at least one parameter is an integer or two or more parameters are separated by an integer. The result is a collection of very general identities (or techniques) that an analyst seeking to evaluate a particular 3F2(1), might want to consider as a starting point. That is the secondary goal. Along the way however, the temptation arose to investigate at least one of the unanswered questions that others have raised. This led to a few digressions, and some possibly new results. The reader is invited to follow where curiosity led me to depart from a straightforward review of the state-of-the-art.
2601.04425Jan 2026
View2601.03987An SU(2n)-valued nonlinear Fourier transform
We define a nonlinear Fourier transform which maps sequences of contractive $n \times n$ matrices to $SU(2n)$-valued functions on the circle $\mathbb{T}$. We characterize the image of finitely supported sequences and square-summable sequences on the half-line, and construct an inverse for $SU(2n)$-valued functions whose diagonal $n \times n$ blocks are outer matrix functions. As an application, we relate this nonlinear Fourier transform with quantum signal processing over $U(2n)$ and multivariate quantum signal processing.
2601.03987Jan 2026
View
$H^1$ to $L^q$-boundedness of fractional integral operators having a flag kernel
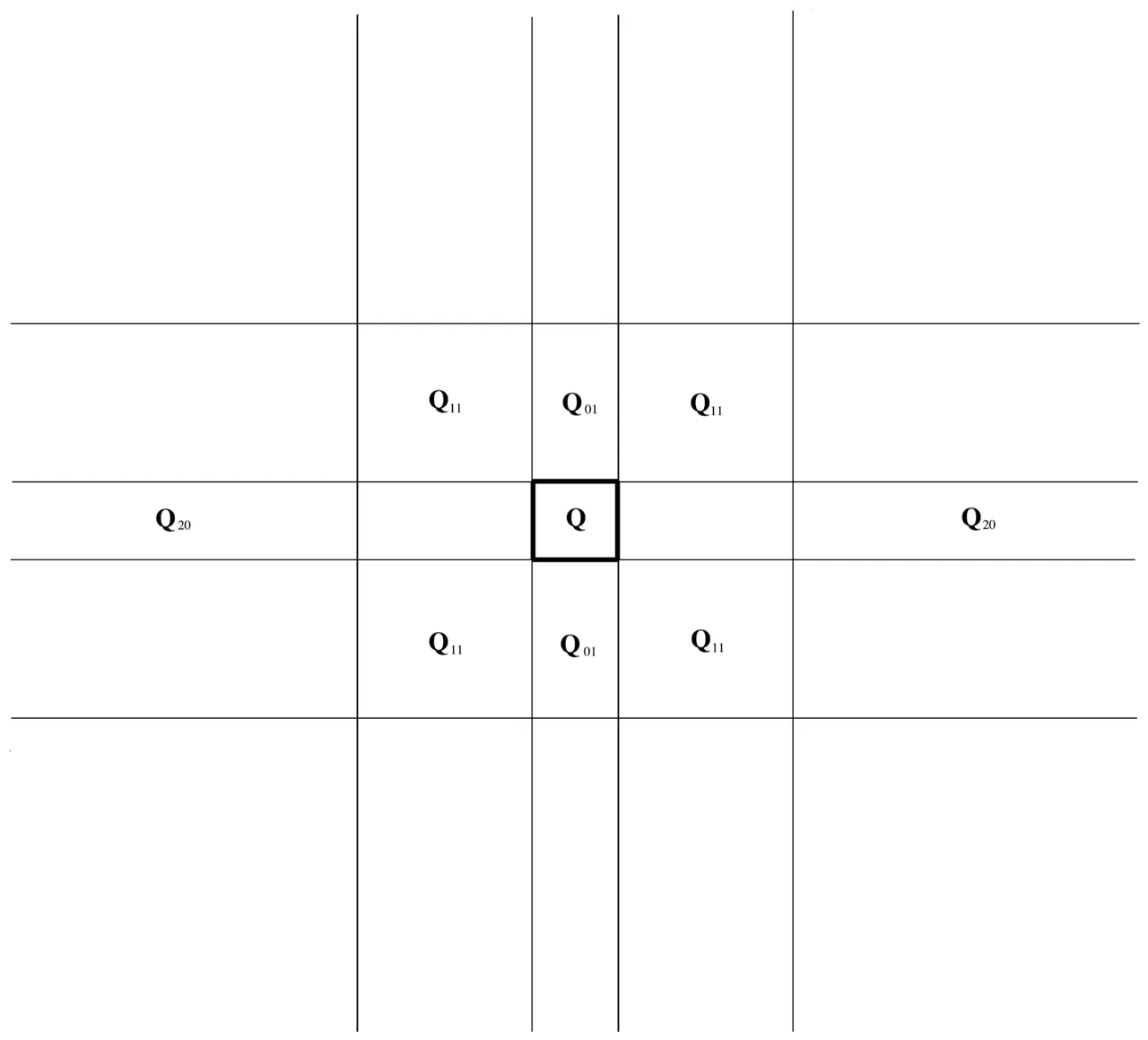
We study a family of fractional integral operators whose kernels satisfying an non-isotropic dilation have singularity on a coordinate subspace. A characterization is given for these operators bounded from the classical, atom decomposable $H^1$-Hardy space to $L^q$-spaces.
2601.03695Jan 2026
View
On Constructions of full-dimensional absolutely normal sets of uniqueness
We construct a class of homogeneous Cantor-Moran measures with all contraction ratios being reciprocal of integers, and prove that they are pointwise absolutely normal. Our approach relies on methods developed by Davenport, Erd{ő}s, and LeVeque \cite{DEL1963} and properties of the order of integers in the multiplicative groups. The construction of these measures differs from the class of pointwise absolutely normal self-similar measures introduced by Hochman and Shmerkin \cite{Hochman2015}, in which dynamical approaches were used. As an application, for all gauge functions $\varphi(r)$ with $r/\varphi(r)\to 0$ as $r\to 0$, we obtain a set of uniqueness $K$ with ${\mathcal H}^{\varphi}(K)>0$. Moreover, we show that there exists a pointwise absolutely normal measure $ μ$ of dimension one fully supported on $K$. The result demonstrates that having a lot of absolutely normal numbers in a Cantor set, even with dimension one, cannot guarantee that it supports a measure with Fourier decay. It also shows that the ${\mathsf{DEL}}$ criterion being satisfied for all integers does not guarantee any Fourier decay nor the supporting set is a set of multiplicity.
2601.03402Jan 2026
View2601.02866New biorthogonal sequences generated by index integrals of the weight functions
We exhibit new biorthogonal sequences generated by index integrals of the squares of the modified Bessel functions and gamma functions. The composition orthogonality, involving differential operators is employed. Generalized Wilson polynomials are introduced. Some properties are investigated.
2601.02866Jan 2026
View
Polynomial-order oscillations in geometric discrepancy
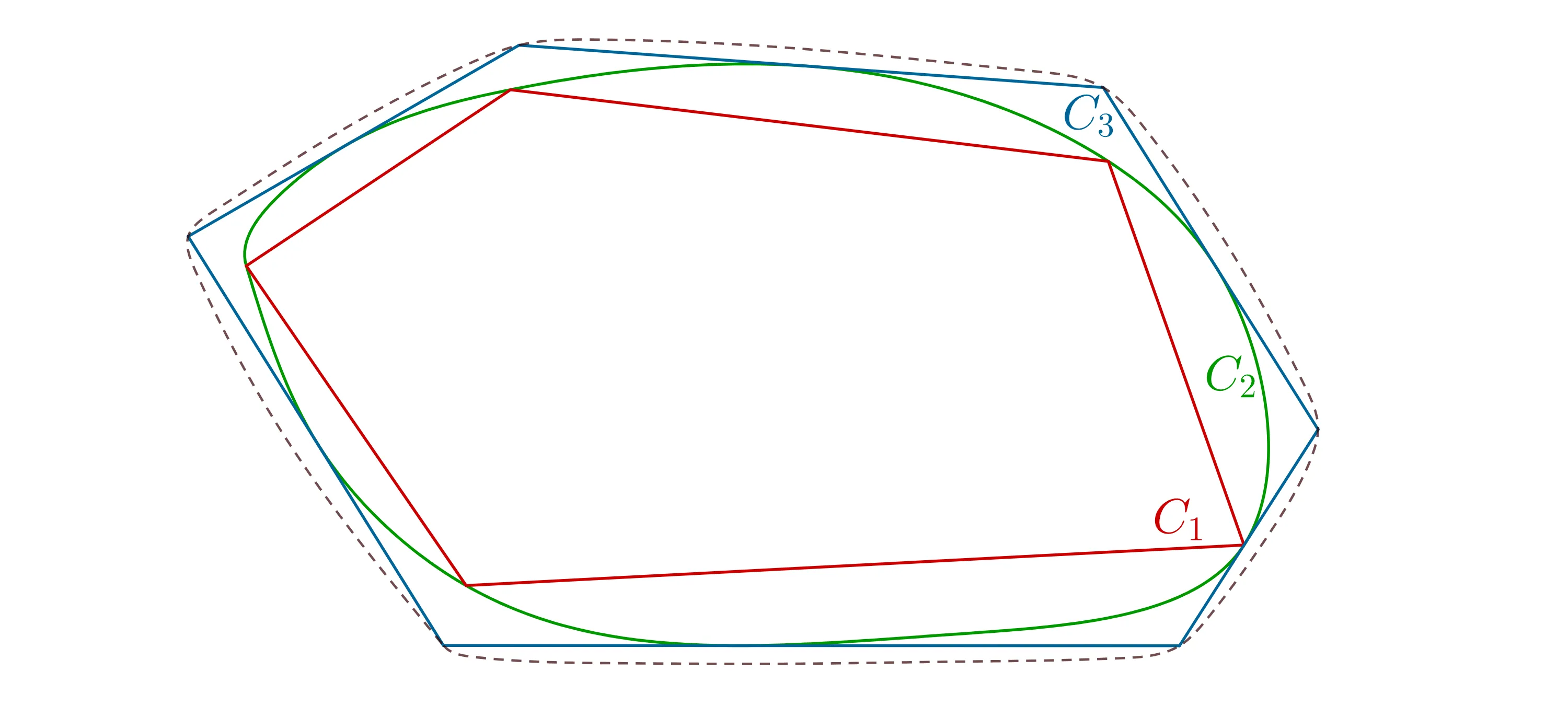
Let $C\subset\mathbb{R}^2$ be a convex body, and let $\mathcal{P}\subset[0,1)^2$ be a set of $N$ points. The discrepancy of $\mathcal{P}$ with respect to $C$ is defined as \begin{equation*} \mathcal{D}(\mathcal{P},\, C)=\sum_{\mathbf{p}\in\mathcal{P}}\sum_{\mathbf{n}\in\mathbb{Z}^2}\mathds{1}_C(\mathbf{p}+\mathbf{n})-N|C|. \end{equation*} A standard approach for estimating how a point distribution deviates from uniformity is to average the latter quantity over a family of sets; in particular, when considering quadratic averages over translations and dilations, one obtains \begin{equation*} \mathcal{D}_2(\mathcal{P},\, C)=\int_{0}^{1}\int_{[0,1)^2}\left|\mathcal{D}( \mathcal{P},\,\boldsymbolτ+δC)\right|^2\,{\rm d}\boldsymbolτ\,{\rm d} δ. \end{equation*} This paper concerns the behaviour of optimal \textit{homothetic quadratic discrepancy} \begin{equation*} \inf_{\# \mathcal{P}=N} \mathcal{D}_2(\mathcal{P},\, C)\quad\text{as}\quad N\to+\infty. \end{equation*} Beck and Chen \cite{MR1489133} showed that the optimal \textit{h.q.d.} of convex polygons has an order of growth of $\log N$. More recently, Brandolini and Travaglini \cite{MR4358540} showed that the optimal \textit{h.q.d.} of planar convex bodies has an order of growth of $N^{1/2}$ if their boundary is $\mathcal{C}^2$, and of $N^{2/5}$ if their boundary is only piecewise-$\mathcal{C}^2$ and not polygonal. We show that, in general, no order of growth is required. First, by an implicit geometric construction, we show that one can obtain prescribed oscillations from a logarithmic order of $\log N$ to polynomial orders of $N^{2/5}$ and $N^{1/2}$, and vice versa. Secondly, by using Fourier-analytic methods, we show that prescribed polynomial-order oscillations in the range $N^α$ with $α\in(2/5,1/2)$ are achievable.
2601.02335Jan 2026
View2601.01880Maximal averages and non-transversality
We investigate the $L^p$ mapping properties of maximal functions associated with analytic hypersurfaces in $\mathbb R^d$, with a particular emphasis on the role of transversality. Around points that are not transversal, we show that the associated maximal function is bounded on $L^p(\mathbb R^d)$ for all $p>2$, regardless of the decay of the Fourier transform of surface measures. In contrast, away from non-transversal points, we prove that $L^p$ bounds for the maximal operator imply that the Fourier transform of the surface measure decays at rate $1/q$ for $q>p$. Combining these two regimes, we demonstrate that the conjecture of Stein and Iosevich-Sawyer on maximal functions could be re-formulated, in the analytic setting, by restricting attention to transversal points. Moreover, our result completely settles the refined form of the conjecture for certain cases.
2601.01880Jan 2026
View2601.01821The Anisotropic Balian-Low Phenomenon and the Variational Construction of Wavelet Frames
This paper investigates the stability of wavelet frames within anisotropic function spaces. By replacing classical integral estimates with a matrix algebra approach, we establish the boundedness of frame operators and derive optimal dual wavelets via variational principles. Our analysis reveals fundamental geometric obstructions, identified here as an anisotropic Balian-Low phenomenon, which preclude the existence of tight frames for isotropic generators in high-shear regimes. Furthermore, we apply these results to determine sharp constants for Sobolev embeddings, explicitly quantifying the impact of dilation geometry on analytic stability.
2601.01821Jan 2026
View2601.01203On oscillator death in the Winfree model I: the one-dimensional case
We show that for the standard sinusoidal Winfree model, a coupling strength exceeding twice the maximal magnitude of the intrinsic frequencies guarantees the convergence of the system for Lebesgue almost every initial data. This is proven by first showing, via an order parameter bootstrapping argument, that the pathwise critical coupling strength is upper bounded by a function of the order parameter, and then showing by a volumetric argument that for Lebesgue almost every data the order parameter cannot stay below and be bounded away from 1 for all time; this is a Winfree model counterpart of the analysis of Ha and the author (2020) performed for the Kuramoto model. Using concentration of measure and the aforementioned volumetric argument, we show that, except possibly on a set of very small measure, oscillator death is observed in finite time; this rigorously demonstrates the existence of the oscillator death regime numerically observed by Ariaratnam and Strogatz (2001). These results are robust under many other choices of interaction functions often considered for the Winfree model. We demonstrate that the asymptotic dynamics described in this paper are sharp by analyzing the equilibria of the Winfree model, and we bound the total number of equilibria using a polynomial description. The sequel to this paper will deal with the Winfree model on higher-dimensional manifolds, such as the Euclidean spheres and the unitary groups.
2601.012031Jan 2026
View2601.01182Approximation of generalized Wiener classes of functions of several variables in different metrics
The paper presents new and known results on estimates of important linear and nonlinear approximation characteristics of generalized Wiener classes of functions of several variables in different metrics.
2601.01182Jan 2026
View2601.01032Necessary conditions for weighted estimates of Multilinear Multipliers and Pseudo-Differential Operators
We study optimal multiple weight assumptions in the weighted theory of multilinear Fourier multipliers and multilinear pseudo-differential operators. For multilinear Fourier multipliers, we revisit the weighted Hörmander-type theorem of Li and Sun, as a multilinear version of Kurtz and Wheeden, and show that their multiple weight condition is sharp. This provides the sharp necessary condition in the multilinear setting and simultaneously improves the classical linear necessity established by Kurtz and Wheeden. In the pseudo-differential setting, we consider recent weighted estimates of the authors for symbols in the multilinear Hörmander class and prove that their multiple weight hypothesis is also best possible. As a corollary, we can obtain the optimality of sharp maximal function estimates for multilinear pseudo-differential operators in the papers of the authors which originated from the results of Chanillo and Torchinsky.
2601.01032Jan 2026
View2601.00721Symbolic Integration of Differential Forms: From Abel to Zeilberger
This paper focuses on symbolic integration of differential forms, with a particular emphasis on historical and modern developments, from Abel's addition theorems for Abelian integrals to Zeilberger's creative telescoping for parameterized integrals. It explores closed rational $p$-forms and provides algorithmic approaches for their integration, extending classical results like Hermite reduction and Liouville's theorem. The integration of closed differential forms with parameters is further examined through telescopers, offering a unified framework for handling both algebraic and transcendental cases.
2601.00721Jan 2026
View2601.00201A note on characterization of $H^1$ Sobolev spaces by square functions
We establish characterization of $H^1$ Sobolev spaces by certain square functions, improving previous results.
2601.00201Jan 2026
View2601.00902Optimal Hardy Inequality for Fractional Laplacians on the Lattice
We study the fractional Hardy inequality on the integer lattice. We prove null-criticality of the Hardy weight and hence optimality of the constant. More specifically, we present a family of Hardy weights with respect to a parameter and show that below a certain threshold the Hardy weight is positive critical while above the threshold it is subcritical. In particular, the Hardy weight at the threshold is optimal in the sense that any larger weight would fail to be a Hardy weight and the Hardy inequality does not allow for a minimizer. A crucial ingredient in our proof is an asymptotic expansion of the fractional discrete Riesz kernel.
2601.00902Dec 2025
View2512.24990The Fourier extension conjecture for the paraboloid
We give a proof of Fourier extension conjecture on the paraboloid in all dimensions bigger than 2 that begins with a decomposition suggested in Sawyer [Saw8] of writing a smooth Alpert projection as a sum of pieces whose Fourier extensions are localized. This is then used in the case d=3 to establish the trilinear equivalence of the Fourier extension conjecture given in C. Rios and E. Sawyer [RiSa1] and [RiSa3]. A key aspect of the proof is that the trilinear equivalence only requires an averaging over grids, which converts a difficult exponential sum into an oscillatory integral with periodic amplitude, that is then used to prove the localization on the Fourier side. Finally, we extend this argument to all dimensions bigger than 2 using bilinear analogues of the smooth Alpert trilinear inequalities, which generalize those in Tao, Vargas and Vega [TaVaVe].
2512.24990Dec 2025
View
From Complex-Analytic Models to Sparse Domination: A Dyadic Approach of Hypersingular Operators via Bourgain's Interpolation Method
Motivated by the work of Cheng--Fang--Wang--Yu on the hypersingular Bergman projection, we develop a real-variable and dyadic framework for hypersingular operators in regimes where strong-type estimates fail at the critical line. The main new input is a hypersingular sparse domination principle combined with Bourgain's interpolation method, which provides a flexible mechanism to establish critical-line (and endpoint) estimates. In the unit disc setting with $1<t<3/2$, we obtain a full characterization of the $(p,q)$ mapping theory for the dyadic hypersingular maximal operator $\mathcal M_t^{\mathcal D}$, in particular including estimates on the critical line $1/q-1/p=2t-2$ and a weighted endpoint criterion in the radial setting. We also prove endpoint estimates for the hypersingular Bergman projection \[ K_{2t}f(z)=\int_{\mathbb D}\frac{f(w)}{(1-z\overline w)^{2t}}\,dA(w), \] including a restricted weak-type bound at $(p,q)=\bigl(\tfrac{1}{3-2t},1\bigr)$. Finally, we introduce a class of hypersingular cousin of sparse operators in $\mathbb R^n$ associated with \emph{graded} sparse families, quantified by the sparseness $η$ and a new structural parameter (the \emph{degree}) $K_{\mathcal S}$, and we characterize the corresponding strong/weak/restricted weak-type regimes in terms of $(n,t,η,K_{\mathcal S})$. Our real-variable perspective addresses to an inquiry raised by Cheng--Fang--Wang--Yu on developing effective real-analytic tools in the hypersingular regime for $K_{2t}$, and it also provides a new route toward the critical-line analysis of Forelli--Rudin type operators and related hypersingular operators in both real and complex settings.
2512.24972Dec 2025
ViewPage 1 of 21
