Analysis & PDEs

Partial differential equations, functional analysis, and harmonic analysis

Includes:Analysis of PDEs(math.AP)Functional Analysis(math.FA)Classical Analysis and ODEs(math.CA)

Trending in Analysis & PDEs

2512.01966

Semigroups For Initial-Boundary Value Problems

We review the theory of one-sided coupled operator matrices with a focus on evolution equations with inhomogeneous boundary conditions. (The original article had no abstract.)

2512.0196617

Dec 2025Analysis of PDEs

Absence of Exponential Stability and Polynomial Stabilization in a Class of Beam Models with Tip Rotary Inertia

We investigate the impact of dissipative dynamic boundary conditions applied at one end of a beam, analyzing their influence on model stability within the Euler-Bernoulli framework. Our primary finding is that hybrid dissipation does not alter the decay characteristics of the original model. We examine two scenarios: first, when hybrid dissipation is the sole dissipative mechanism, and second, when it complements other dissipative mechanisms. In the first case, we demonstrate that hybrid dissipation fails to induce exponential decay, instead producing a slow decay rate of $t^{-1/2}$ for large $t$. In the second case, when acting as a complementary mechanism, hybrid dissipation neither enhances nor diminishes the decay behavior of the original model.

2512.01964

Dec 2025Analysis of PDEs

3,188 papers

2601.05211

A non-commutative de Branges-Rovnyak model for row contractions

We extend the de Branges-Rovnyak model for completely non-coisometric (CNC) linear contractions on a Hilbert space to the non-commutative multivariate setting of CNC row contractions. Namely, we show that any CNC contraction from several copies of a Hilbert space into a single copy is unitarily equivalent to the adjoint of the restricted backward right shifts acting on the de Branges-Rovnyak space of a contractive left multiplier between vector-valued "free Hardy spaces" of square-summable power series in several non-commuting (NC) variables. This contractive, operator-valued left multiplier, the characteristic function of the CNC row contraction, is a complete unitary invariant and it is always column-extreme as a contractive left multiplier. Our construction builds a model reproducing kernel Hilbert space of NC functions using a "non-commutative resolvent" of the row contraction, $T$, which is the inverse of the monic, affine linear pencil of $T$ in a certain NC unit row-ball of the NC universe of all row tuples of square matrices of all finite sizes.

2601.05211Jan 2026

View

2601.05130

Sparsity and uniform regularity for regularised optimal transport

We consider regularised quadratic optimal transport with subquadratic polynomial or entropic regularisation. In both cases, we prove interior Lipschitz-estimates on a transport-like map and interior gradient Lipschitz-estimates on the potentials, under the assumption that the transport map solving the unregularised problem is bi-$C^{1,α}$-regular. For strictly subquadratic and entropic regularisation, the estimates improve to interior $C^1$ and $C^2$ estimates for the transport-like map and the potentials, respectively. Our estimates are uniform in the regularisation parameter. As a consequence of this, we obtain convergence of the transport-like map (resp. the potentials) to the unregularised transport map (resp. Kantorovich potentials) in $C^{0,1-}_{\mathrm{loc}}$ (resp. $C^{1,1-}_{\mathrm{loc}}$). Central to our approach are sharp local bounds on the size of the support for regularised optimal transport which we derive for a general convex, superlinear regularisation term. These bounds are of independent interest and imply global bias bounds for the regularised transport plans. Our global bounds, while not necessarily sharp, improve on the best known results in the literature for quadratic regularisation.

2601.05130Jan 2026

View

Non-linear parabolic PDEs with rough data and coefficients: existence, uniqueness and regularity of weak solutions in critical spaces

This article investigates the well-posedness of weak solutions to non-linear parabolic PDEs driven by rough coefficients with rough initial data in critical homogeneous Besov spaces. Well-posedness is understood in the sense of existence and uniqueness of maximal weak solutions in suitable weighted $Z$-spaces in the absence of smallness conditions. We showcase our theory with an application to rough reaction--diffusion equations. Subsequent articles will treat further classes of equations, including equations of Burgers-type and quasi-linear problems, using the same approach. Our toolkit includes a novel theory of hypercontractive singular integral operators (SIOs) on weighted $Z$-spaces and a self-improving property for super-linear reverse Hölder inequalities.

2601.05080Jan 2026

View

On the effects of protection zone and directed population flux in prey-predator dynamics

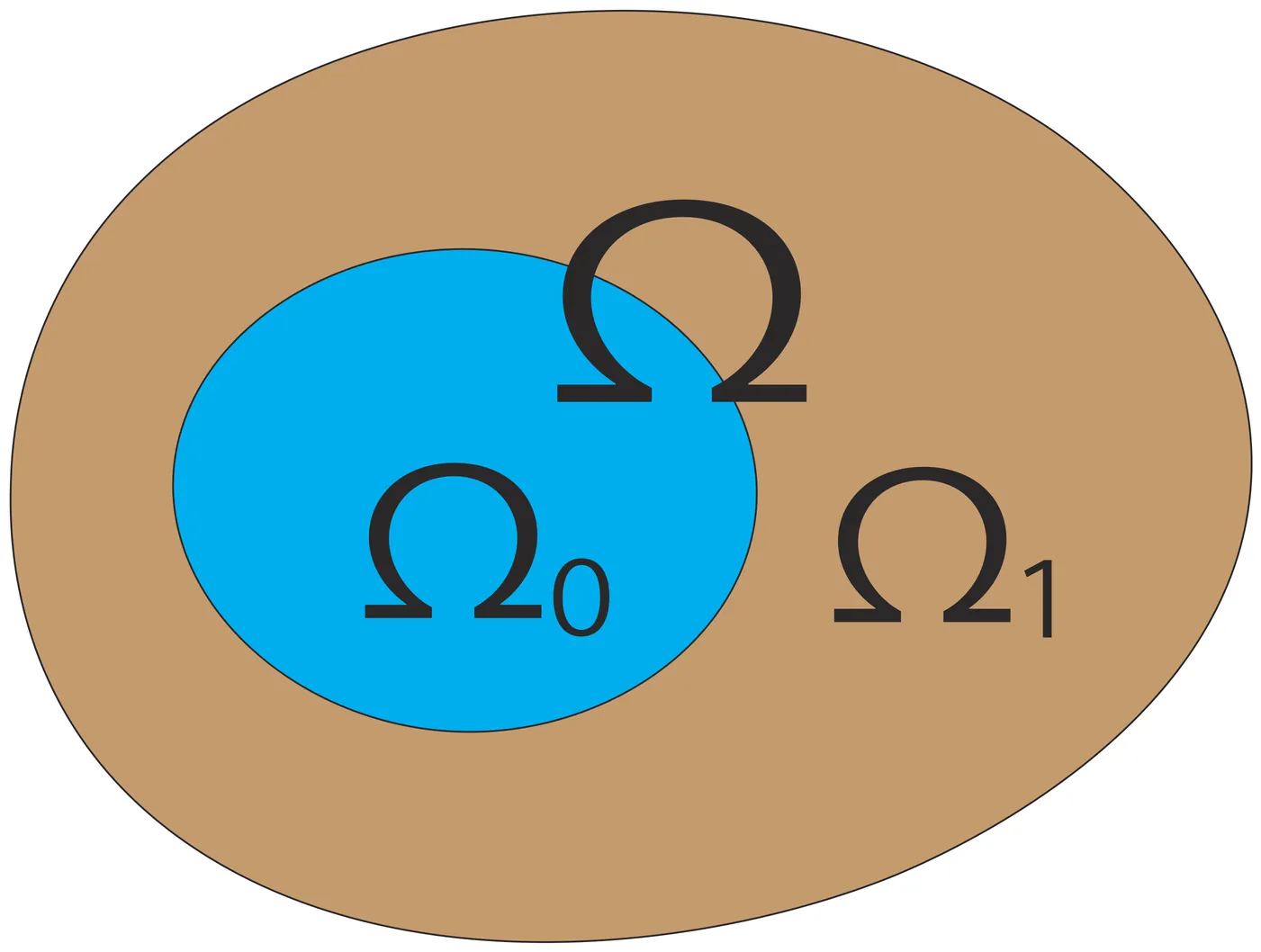
We study a spatial predator-prey model in which prey can enter a protection zone (refuge) inaccessible to predators, while predators exhibit directed movement toward prey-rich regions. The directed movement is modeled by a far-sighted population flux motivated by classical movement rules, in contrast to the more commonly analyzed near-sighted chemotaxis-type mechanisms. We first establish local-in-time well-posedness for the corresponding nonstationary problem under Neumann boundary conditions, despite the discontinuity induced by the refuge interface. We then investigate the stationary problem, focusing on how the coexistence states emerge and organize globally in parameter space. In particular, we identify the bifurcation threshold for positive steady states from semitrivial predator-only equilibria, and describe the global continuation of the resulting branches. Our analysis reveals that strong directed movement can induce turning-point structures and multiplicity of coexistence steady states, highlighting a nontrivial interplay between spatial protection and predator movement behavior.

2601.05054Jan 2026

View

2601.05023

Finite-time blow-up in a quasilinear two-species chemotaxis system with two chemicals

This paper investigates the finite-time blow-up phenomena to a quasilinear two-species chemotaxis system with two chemicals \begin{align}\tag{$\star$} \begin{cases} u_t = \nabla \cdot \left(D_1(u) \nabla u\right) - \nabla \cdot \left(u \nabla v\right), & x \in Ω, \ t > 0, 0 = Δv - μ_2 + w, \quad μ_2=\fint_Ωw, & x \in Ω, \ t > 0, w_t = \nabla \cdot \left(D_2(w) \nabla w\right) - \nabla \cdot \left(w \nabla z\right), & x \in Ω, \ t > 0, 0 = Δz - μ_1 + u, \quad μ_1=\fint_Ωu, & x \in Ω, \ t > 0, \frac{\partial u}{\partial ν} = \frac{\partial v}{\partial ν} = \frac{\partial w}{\partial ν} = \frac{\partial z}{\partial ν} = 0, & x \in \partial Ω, \ t > 0, u(x, 0) = u_0(x), \quad w(x, 0) = w_0(x), & x \in Ω, \end{cases} \end{align} where $Ω\subset \mathbb{R}^n$ $(n \geqslant 3)$ is a smoothly bounded domain. The nonlinear diffusion functions $ D_1(s) $ and $ D_2(s) $ are of the following forms: \begin{align*} D_1(s)\simeq s^{m_1-1} \quad \text{and}\quad D_2(s) \simeq s^{m_2-1}, \quad m_1,m_2> 1 \end{align*} for $s\geqslant 1$. For the classical two-species chemotaxis system with two chemicals (i.e. the second and fourth equations are replaced by $0 = Δv - v + w$ and $0 = Δz - z + u$ ), Zhong [J. Math. Anal. Appl., 500 (2021), Paper No. 125130, pp. 22.] showed that the system possesses a globally bounded classical solution in the case that \[ m_1 + m_2 < \max\left\{m_1m_2 + \frac{2m_1}{ n},\ m_1m_2 + \frac{2m_2 }{ n}\right\}. \] Complementing the boundedness result, we prove that the system ($\star$) admits solutions that blow up in finite time, if \[ m_1 + m_2 > \max\left\{ m_1m_2 + \frac{2m_1}{ n},\ m_1m_2 + \frac{2m_2}{ n}\right\} \] with $n\geqslant 3$.

2601.05023Jan 2026

View

2601.05015

Nodal set comparison for Allen--Cahn solutions with conical asymptotics

We establish a comparison principle for entire solutions of the Allen--Cahn equation whose nodal sets, possibly singular, are asymptotic to a regular minimizing hypercone. We show that inclusion of the positive phases enforces a global ordering of the solutions. As a consequence, the positive phase uniquely determines the solution, and strict phase inclusion implies that the corresponding nodal sets are disjoint. Our analysis relies on a maximum principle for the linearized operator on unbounded domains that are not necessarily smooth, and yields an Allen--Cahn analogue of the strong maximum principle for minimal hypersurfaces.

2601.05015Jan 2026

View

Critical blow-up curve in a two-species chemotaxis system with two chemicals involving flux-limitation

We investigate the following two-species chemotaxis system with two chemicals involving flux-limitation \begin{align}\tag{$\star$} \begin{cases} u_t = Δu - \nabla \cdot \left(u(1+|\nabla v|^2)^{-\frac{p}{2}}\nabla v\right), & x \in Ω, \ t > 0, \\ 0 = Δv - μ_w + w, \quad μ_{w}=f_Ω w, & x \in Ω, \ t > 0, \\ w_t = Δw - \nabla \cdot \left(w (1+|\nabla z|^2)^{-\frac{q}{2}} \nabla z\right), & x \in Ω, \ t > 0, \\ 0 = Δz - μ_u + u, \quad μ_{u}=f_Ω u, & x \in Ω, \ t > 0, \\ \frac{\partial u}{\partial ν} = \frac{\partial v}{\partial ν} = \frac{\partial w}{\partial ν} = \frac{\partial z}{\partial ν} = 0, & x \in \partial Ω, \ t > 0, \\ u(x, 0) = u_0(x), \quad w(x, 0) = w_0(x), & x \in Ω, \end{cases} \end{align} where $p,q \in \mathbb{R}$ and $Ω\subset \mathbb{R}^n$ is a smooth bounded domain. In this paper, we identify a critical blow-up curve ( i.e $p=\frac{n-2}{n-1}$ and $q=\frac{n-2}{n-1}$ in the square $(0,\frac{n-2}{n-1}] \times (0,\frac{n-2}{n-1}]$) for system ($\star$) with $n\geq 3$ and $p,q>0$. Specifically, \begin{itemize} \item when $Ω=B_R(0) \subset \mathbb{R}^n$ with $n\geq 3$, if $0<p<\frac{n-2}{n-1}$ and $0<q<\frac{n-2}{n-1}$, there exist radially symmetric initial data such that the corresponding solution blows up in finite time; \item for any general smooth bounded domain, if either $n=1$ ( with $p,q \in \mathbb{R}$ arbitrary) or $n\geq 2$ with $p>\frac{n-2}{n-1}$ or $q>\frac{n-2}{n-1}$, then solutions exist globally and remain bounded. \end{itemize}

2601.05008Jan 2026

View

Critical blow-up lines in a two-species quasilinear chemotaxis system with two chemicals

In this study, we explore the quasilinear two-species chemotaxis system with two chemicals \begin{align}\tag{$\star$} \begin{cases} u_t = \nabla \cdot(D(u)\nabla u) - \nabla \cdot \left(S(u) \nabla v\right), & x \in Ω, \ t > 0, \\ 0 = Δv - μ_w + w, \quad μ_w=\fint_Ωw, & x \in Ω, \ t > 0, \\ w_t = Δw - \nabla \cdot \left(w \nabla z\right), & x \in Ω, \ t > 0, \\ 0 = Δz - μ_u + u, \quad μ_u=\fint_Ωu, & x \in Ω, \ t > 0, \\ \frac{\partial u}{\partial ν} = \frac{\partial v}{\partial ν} = \frac{\partial w}{\partial ν} = \frac{\partial z}{\partial ν} = 0, & x \in \partial Ω, \ t > 0, \\ u(x, 0) = u_0(x), \quad w(x, 0) = w_0(x), & x \in Ω, \end{cases} \end{align} where $Ω\subset \mathbb{R}^n$ ($n \geq3$) is a smooth bounded domain. The functions $D(s)$ and $S(s)$ exhibit asymptotic behavior of the form \begin{align*} D(s) \simeq k_D s^p \ \text {and} \ S(s) \simeq k_S s^q, \quad s \gg 1 \end{align*} with $p,q \in \mathbb{R}$. We prove that \begin{itemize} \item when $Ω$ is a ball, if $q-p>2-\frac{n}{2}$ and $q>1-\frac{n}{2}$, there exist radially symmetric initial data $u_0$ and $w_0$, such that the corresponding solutions blow up in finite time; \item for any general smooth bounded domain $Ω\subset \mathbb{R}^n$, if $q-p<2-\frac{n}{2}$, all solutions are globally bounded; \item for any general smooth bounded domain $Ω\subset \mathbb{R}^n$, if $q<1-\frac{n}{2}$, all solutions are global. \end{itemize} We point out that our results implies that the system ($\star$) possess two critical lines $ q-p=2-\frac{n}{2}$ and $q=1-\frac{n}{2}$ to classify three dynamics among global boundedness, finite-time blow-up, and global existence of solutions to system ($\star$).

2601.04994Jan 2026

View

2601.04987

The local Dirichlet integral and applications

We study the local Dirichlet integral of distance functions and their behavior within the harmonic Dirichlet space. We provide estimates for the local Dirichlet integral of distance functions, which allow us to study their membership in the algebra of multipliers of the Dirichlet space. We give sufficient condition for a closed subset of the unit circle to be polar and we also examine cyclicity in the harmonic Dirichlet spaces.

2601.04987Jan 2026

View

2601.04944

On Navier-Stokes equations arising from the rotation of an obstacle in a fluid

We consider the modified Navier-Stokes equations in R3 describing the motion of a fluid in the presence of a rotating rigid body. Weighted Sobolev spaces are used to describe the behavior of solutions at large distances. Under suitable assumptions, w e prove the existence and regularity of solutions satisfying appropriate conditions at infinity.

2601.04944Jan 2026

View

2601.04894

Improved convergence rates in the fast-reaction approximation of the triangular Shigesada-Kawasaki-Teramoto system

We consider the fast-reaction approximation to the triangular Shigesada-Kawasaki-Teramoto model on a bounded domain in the physical dimension $d\le 3$. We provide explicit convergence rates on the whole domain in $\textnormal{L}^\infty\textnormal{L}^2\cap\textnormal{L}^2\textnormal{H}^1$ and in the interior we prove convergence with an explicit rate in any $\textnormal{L}^\infty\textnormal{H}^l$ for all $l > 0$.

2601.04894Jan 2026

View

2601.04893

Convergence of Hermite expansions in modulation spaces

The aim of this paper is to give an elementary proof that Hermite expensions of a function $f$ in the modulation space $M^p(R)$ converges to $f$ in $M^p(R)$ when $1< p<+\infty$ and may diverge when $p = 1,\infty$. The result was previously established for $1< p<+\infty$ by Garling and Wojtaszczyk and for $p = 1,\infty$ by Lusky in an equivalent setting of Fock spaces by different methods. Higher dimesional results are also considered. In an appendix, we also establish upper bounds for the Zak transform of Hermite functions.

2601.04893Jan 2026

View

2601.04845

Boundedness in a two-dimensional doubly degenerate nutrient taxis system with logistic source

We are concerned with the following doubly degenerate nutrient taxis system \begin{align} \begin{cases}\tag{$\star$}\label{eq-0.1} u_t=\nabla\cdot(u v\nabla u)-\nabla\cdot(u^{2} v\nabla v)+u-u^2,\\[1mm] v_t=Δv-u v, \end{cases} \end{align} posed in a bounded smooth domain $Ω\subset\mathbb{R}^2$ under homogeneous Neumann boundary conditions. This model was introduced to describe the aggregation patterns of colonies of \emph{Bacillus subtilis} observed on thin agar plates. Previous results have established global boundedness in one space dimension and, in two dimensions, under additional assumptions such as small initial data or convex domains (see, e.g., M. Winkler, \textit{Trans. Amer. Math. Soc.}, 2021; M. Winkler, \textit{J. Differ. Equ.}, 2024). In the presence of the quadratic degradation term in the logistic growth, which markedly enhances the dissipative structure of the system, and by employing a weighted energy method, we prove that for arbitrary smooth initial data the problem \eqref{eq-0.1} admits a global weak solution that remains uniformly bounded in time.

2601.04845Jan 2026

View

2601.04804

Semiclassical analysis of the magnetic Laplacian on hyperbolic surfaces

The magnetic Laplacian on hyperbolic surfaces provides a rich analytic framework in which a variety of quantum phenomena emerge. The present note, written for the \emph{Proceedings of the Journées EDP 2025}, is a concise overview of the main results obtained in [arXiv:2505.08584] and work in preparation by the author with L. Charles and A. Chabert.

2601.04804Jan 2026

View

2601.04797

The Semigeostrophic-Euler Limit: Lifespan Lower Bounds and $O(\varepsilon)$ Velocity Stability

We study the two-dimensional semigeostrophic (SG$^{\varepsilon}$) system on the torus in the small-amplitude scaling and its convergence to incompressible Euler in the dual (geostrophic) formulation. Within a natural bootstrap regime for the Poisson/Monge-Ampère coupling, we obtain two main results. First, we prove a lifespan lower bound in slow time with a \emph{log-log} gain; in physical time this yields persistence at least on the scale $\varepsilon^{-1}|\log\log \varepsilon|$. Second, on any bootstrap window we establish a strong velocity-stability estimate with rate $O(\varepsilon)$ in $L^2$, complementing Loeper's $O(1/\varepsilon)$ existence time and $\varepsilon^{2/3}$ weak convergence rate. The proofs combine the incompressible transport structure with a sharp elliptic control of the velocity gradient and a flow-based stability argument. Overall, the results give a clean quantitative bridge from SG$^{\varepsilon}$ to Euler that is both longer-lived (by a log-log factor) and quantitatively stable in velocity.

2601.04797Jan 2026

View

Hypocoercivity and metastability of degenerate KFP equations at low temperature

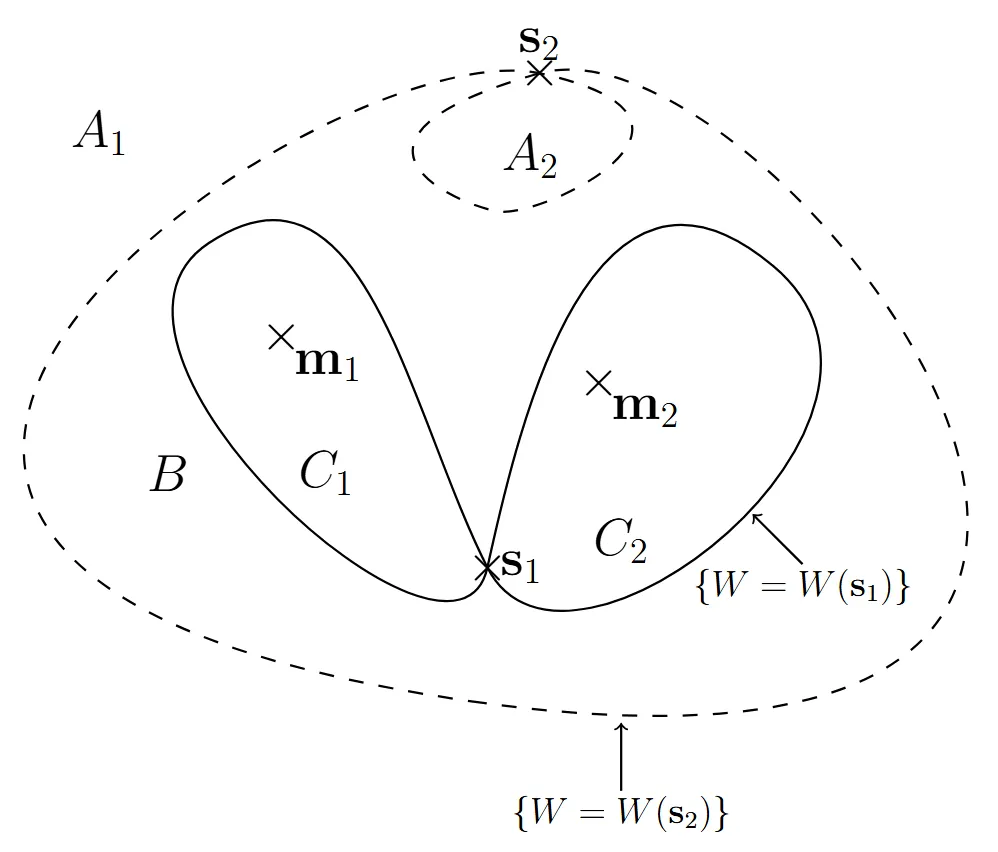
We consider Kramers-Fokker-Planck operators with general degenerate coefficients. We prove semiclassical hypocoercivity estimates for a large class of such operators. Then, we manage to prove Eyring-Kramers formulas for the bottom of the spectrum of some particular degenerate operators in the semiclassical regime, and quantify the spectral gap separating these eigenvalues from the rest of the spectrum. The main ingredient is the construction of sharp Gaussian quasimodes through an adaptation of the WKB method.

2601.04784Jan 2026

View

2601.04783

Szegő Mapping and Hermite--Padé Polynomials for Multiple Orthogonality on the Unit Circle

We investigate generalized Laurent multiple orthogonal polynomials on the unit circle satisfying simultaneous orthogonality conditions with respect to $r$ probability measures or linear functionals on the unit circle. We show that these polynomials can be characterized as solutions of a general two-point Hermite--Padé approximation problem. We derive Szegő-type recurrence relations, establish compatibility conditions for the associated recurrence coefficients, and obtain Christoffel--Darboux formulas as well as Heine-type determinantal representations. Furthermore, by extending the Szegő mapping and the Geronimus relations, we relate these Laurent multiple orthogonal polynomials to multiple orthogonal polynomials on the real line, thereby making explicit the connection between multiple orthogonality on the unit circle and on the real line.

2601.04783Jan 2026

View

2601.04753

Hyperbolic regularization effects for degenerate elliptic equations

This paper investigates the regularity of Lipschitz solutions $u$ to the general two-dimensional equation $\text{div}(G(Du))=0$ with highly degenerate ellipticity. Just assuming strict monotonicity of the field $G$ and heavily relying on the differential inclusions point of view, we establish a pointwise gradient localization theorem and we show that the singular set of nondifferentiability points of $u$ is $\mathcal{H}^1$-negligible. As a consequence, we derive new sharp partial $C^1$ regularity results under the assumption that $G$ is degenerate only on curves. This is done by exploiting the hyperbolic structure of the equation along these curves, where the loss of regularity is compensated using tools from the theories of Hamilton-Jacobi equations and scalar conservation laws. Our analysis recovers and extends all the previously known results, where the degeneracy set was required to be zero-dimensional.

2601.04753Jan 2026

View

2601.04678

The Kato square root estimate with Robin boundary conditions

We prove the Kato square root estimate for second-order divergence form elliptic operators $-div(A\nabla)$ on a bounded, locally uniform domain $D \subseteq \mathbb{R}^n$, for accretive coefficients $A \in L^\infty(D; \mathbb{C}^n)$, under the Robin boundary condition $ν\cdot A\nabla u + bu = 0$ for a (possibly unbounded) boundary conductivity $b$. In contrast to essentially all previous estimates of Kato square root operators, no first-order approach seems possible for the Robin boundary conditions.

2601.04678Jan 2026

View

2601.04622

Liouville-type theorems for the stationary non-Newtonian fluids in a slab

In this paper, we investigate Liouville-type theorems for stationary solutions to the shear thickening fluid equations in a slab. We show that the axisymmetric solution must be trivial if its local $L^\infty$-norm grows mildly as the radius $R$ grows. Also, a bounded general solution $u$ must be trivial if $ru^r$ is bounded. The proof is inspired by the work of Bang, Gui, Wang, and Xie [J. Fluid Mech. 1005 (2025)] for the Navier-Stokes equations, and the key point is to establish a Saint-Venant type estimate that characterizes the growth of the local Dirichlet integral of nontrivial solutions. One new ingredient is the estimate of the constant in Korn's inequality over different domains.

2601.04622Jan 2026

View

Page 1 of 160