Molecular Networks
arXiv:q-bio.MN
Gene regulation, signal transduction, proteomics, metabolomics, network biology.
Looking for a broader view? This category is part of:
24 papers
Thermodynamic Constraints Drive Hierarchical Preemption in Cellular Decision-Making: A Hybrid Petri Net Framework with Application to Bacillus subtilis Sporulation
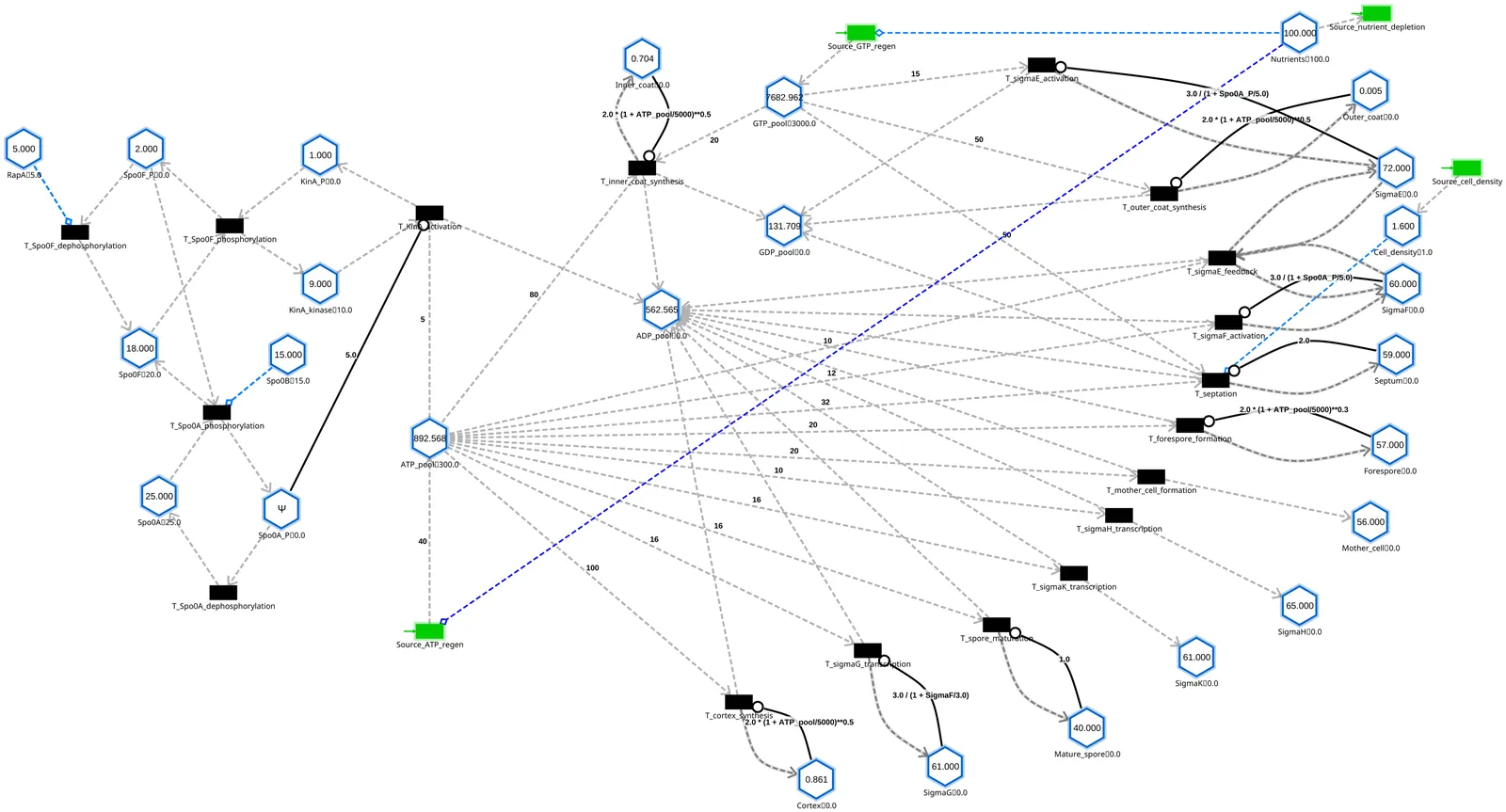
Cellular decision-making under stress involves rapid pathway selection despite energy scarcity. Here we demonstrate that thermodynamic constraints actively drive energy-efficient sporulation, where continuous metabolic sources enable system robustness through dynamic energy management. Using hybrid Petri nets (stochastic transitions with continuous sources) to model Bacillus subtilis sporulation, we show that stress conditions (ATP = 300 mM, 94% depletion) enable sporulation completion with extreme energy efficiency: 0.73 mM ATP per mature spore versus 11.6 mM ATP under normal conditions--a 16-fold efficiency gain. Despite ATP dropping to 1 mM (99.7% depletion) during the crisis, continuous ATP regeneration rescues the system, producing 67 mM mature spores (89% of normal yield) with only 49 mM total ATP consumption. This efficiency emerges from the interplay between stochastic regulatory transitions and continuous metabolic sources, where GTP accumulation (+4974 mM, 166% increase) provides an energy buffer while ATP regeneration (+240 mM) prevents complete depletion. The hybrid Petri net formalism--combining stochastic transitions for regulatory events with continuous sources for metabolic flux--extended with thermodynamic constraints through inhibitor arcs and energy-coupled rate functions, provides the mathematical foundation enabling this discovery by integrating discrete regulatory logic with continuous energy dynamics in a resource-aware concurrency model.
2601.04335Jan 2026
View
Restoring information in aged gene regulatory networks by single knock-ins
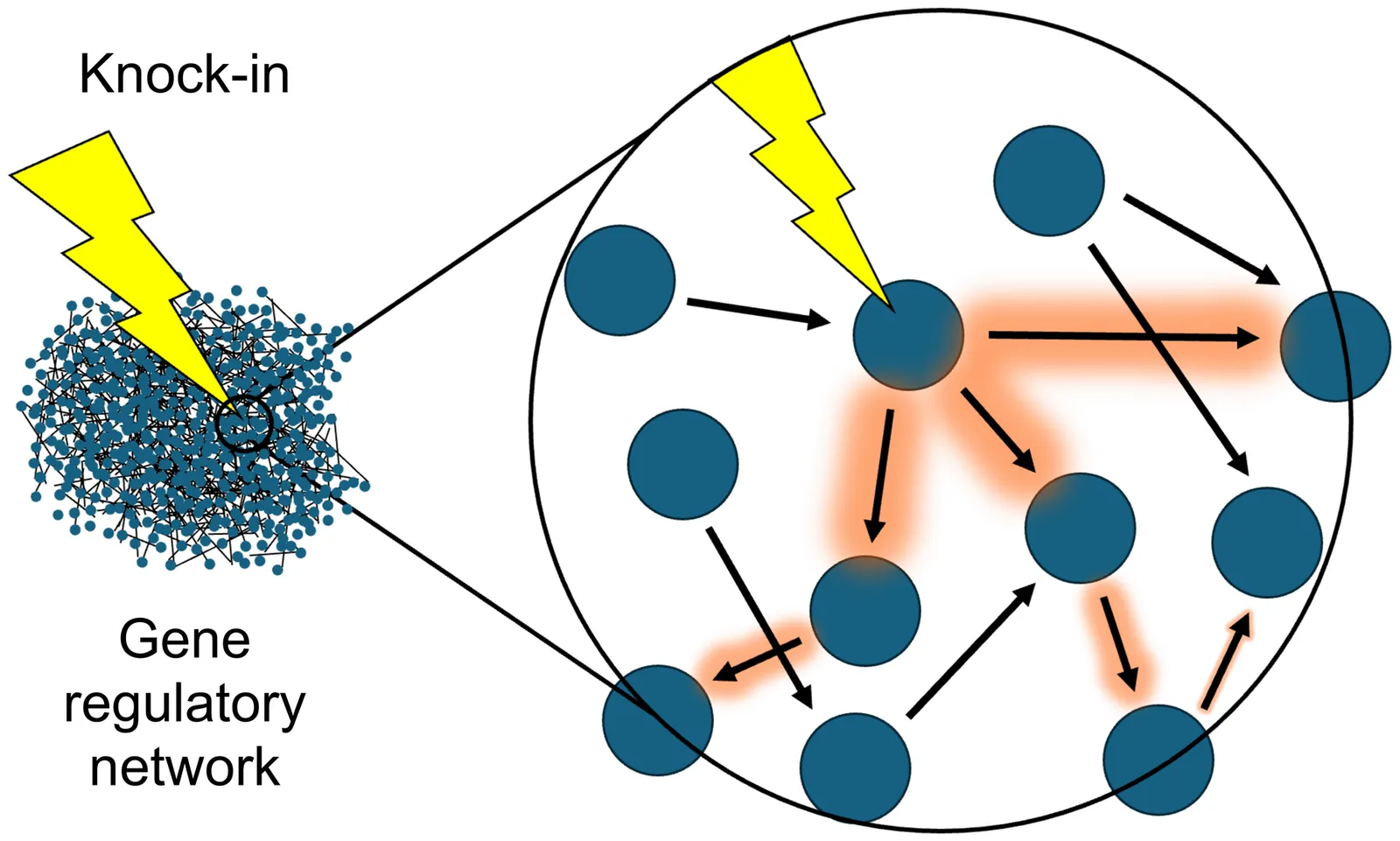
A hallmark of aging is loss of information in gene regulatory networks. These networks are tightly connected, raising the question of whether information could be restored by perturbing single genes. We develop a simple theoretical framework for information transmission in gene regulatory networks that describes the information gained or lost when a gene is "knocked in" (exogenously expressed). Applying the framework to gene expression data from muscle cells in young and old mice, we find that single knock-ins can restore network information by up to 10%. Our work advances the study of information flow in networks and identifies potential gene targets for rejuvenation.
2601.04016Jan 2026
View
Understanding the temperature response of biological systems: Part II -- Network-level mechanisms and emergent dynamics
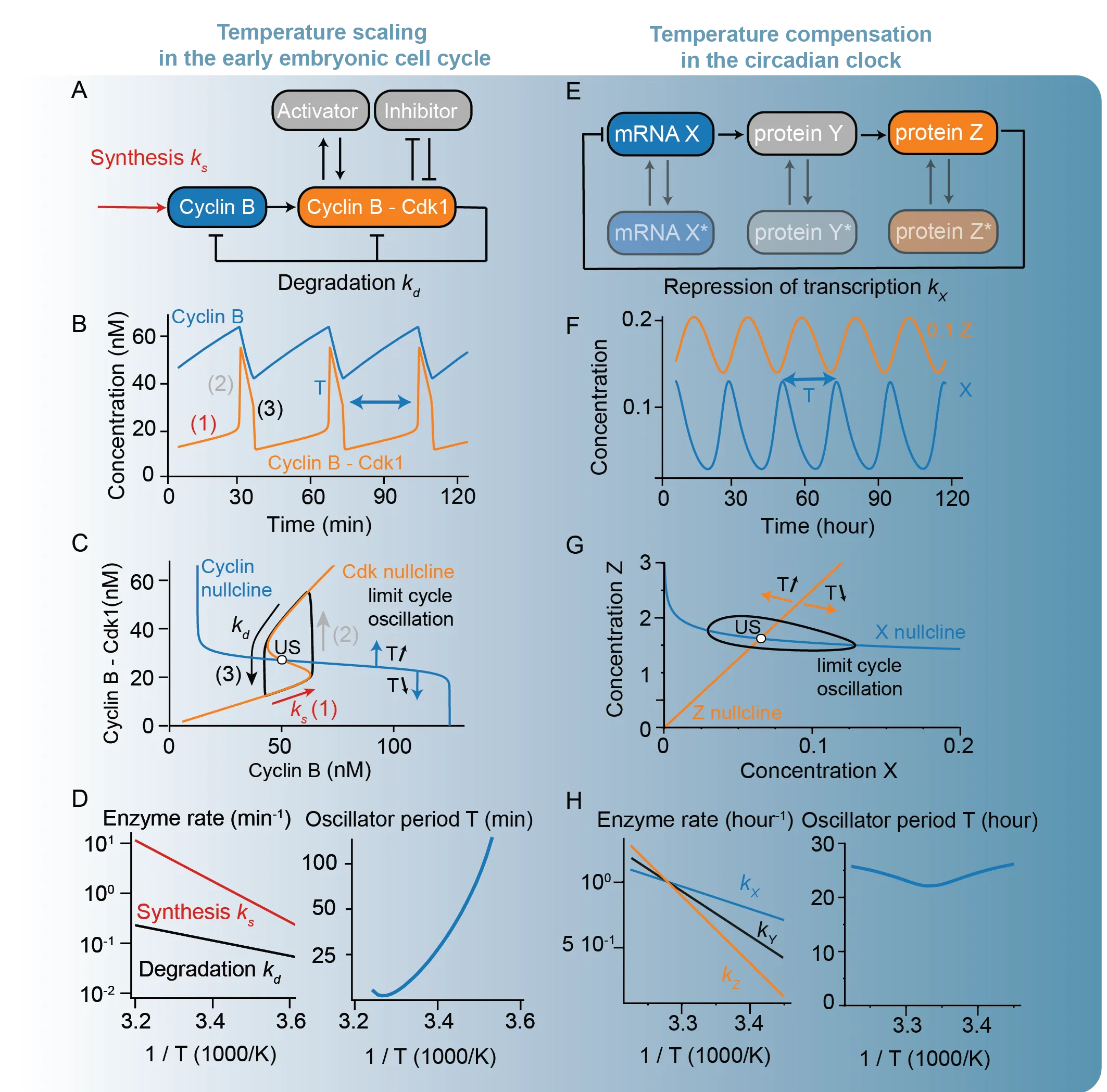
Building on the phenomenological and microscopic models reviewed in Part I, this second part focuses on network-level mechanisms that generate emergent temperature response curves. We review deterministic models in which temperature modulates the kinetics of coupled biochemical reactions, as well as stochastic frameworks, such as Markov chains, that capture more complex multi-step processes. These approaches show how Arrhenius-like temperature dependence at the level of individual reactions is transformed into non-Arrhenius scaling, thermal limits, and temperature compensation at the system level. Together, network-level models provide a mechanistic bridge between empirical temperature response curves and the molecular organization of biological systems, giving us predictive insights into robustness, perturbations, and evolutionary constraints.
2601.03307Jan 2026
View
Allostery Beyond Amplification: Temporal Regulation of Signaling Information
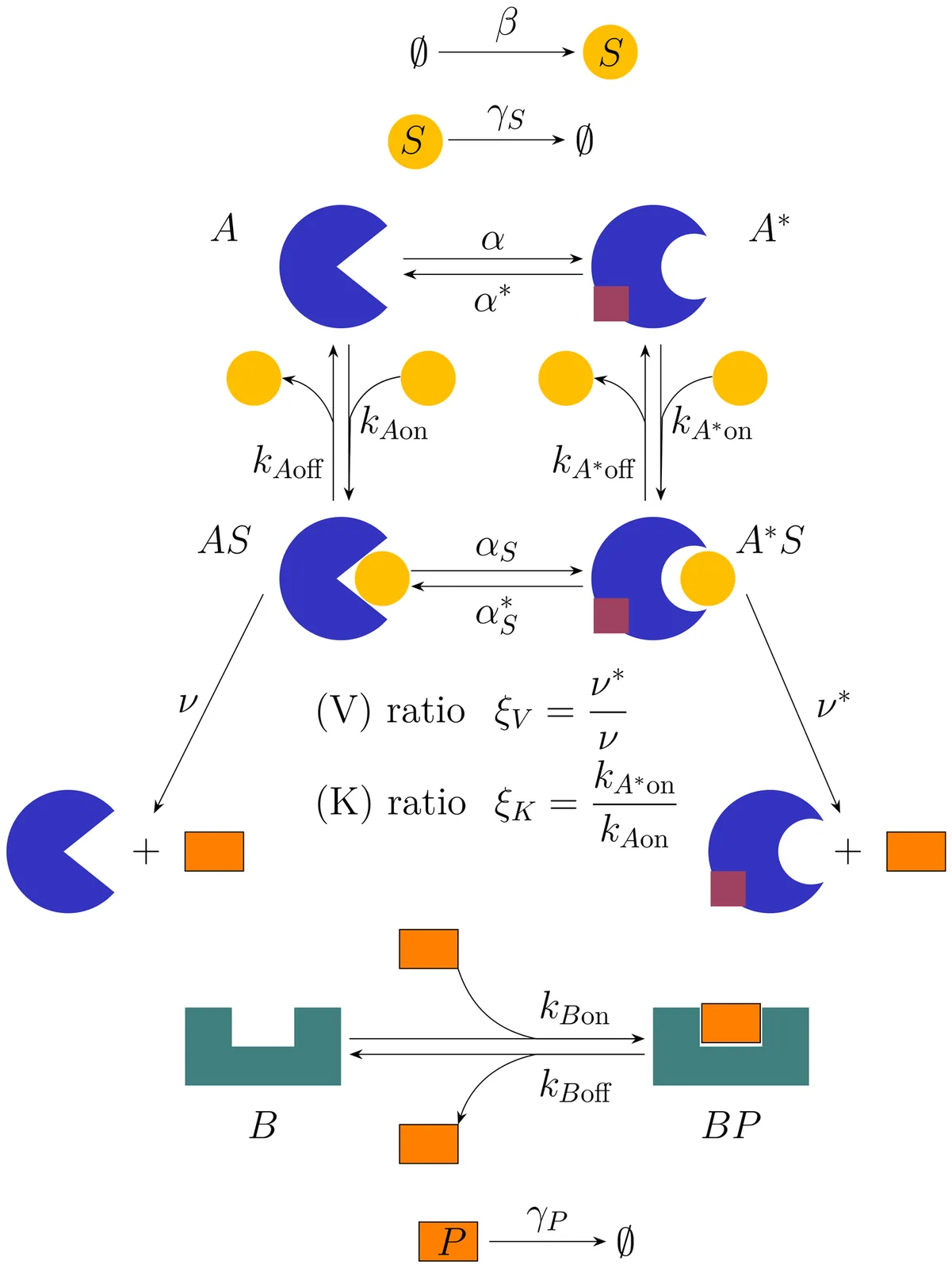
Allostery is a fundamental mechanism of protein regulation and is commonly interpreted as modulating enzymatic activity or product abundance. Here we show that this view is incomplete. Using a stochastic model of allosteric regulation combined with an information-theoretic analysis, we quantify the mutual information between an enzyme's regulatory state and the states of downstream signaling components. Beyond controlling steady-state production levels, allostery also regulates the timing and duration over which information is transmitted. By tuning the temporal operating regime of signaling pathways, allosteric regulation enables distinct dynamical outcomes from identical molecular components, providing a physical mechanism for temporal information flow, signaling specificity, and coordination without changes in metabolic pathways.
2601.01850Jan 2026
View
Saturation-Based Atom Provenance Tracing in Chemical Reaction Networks
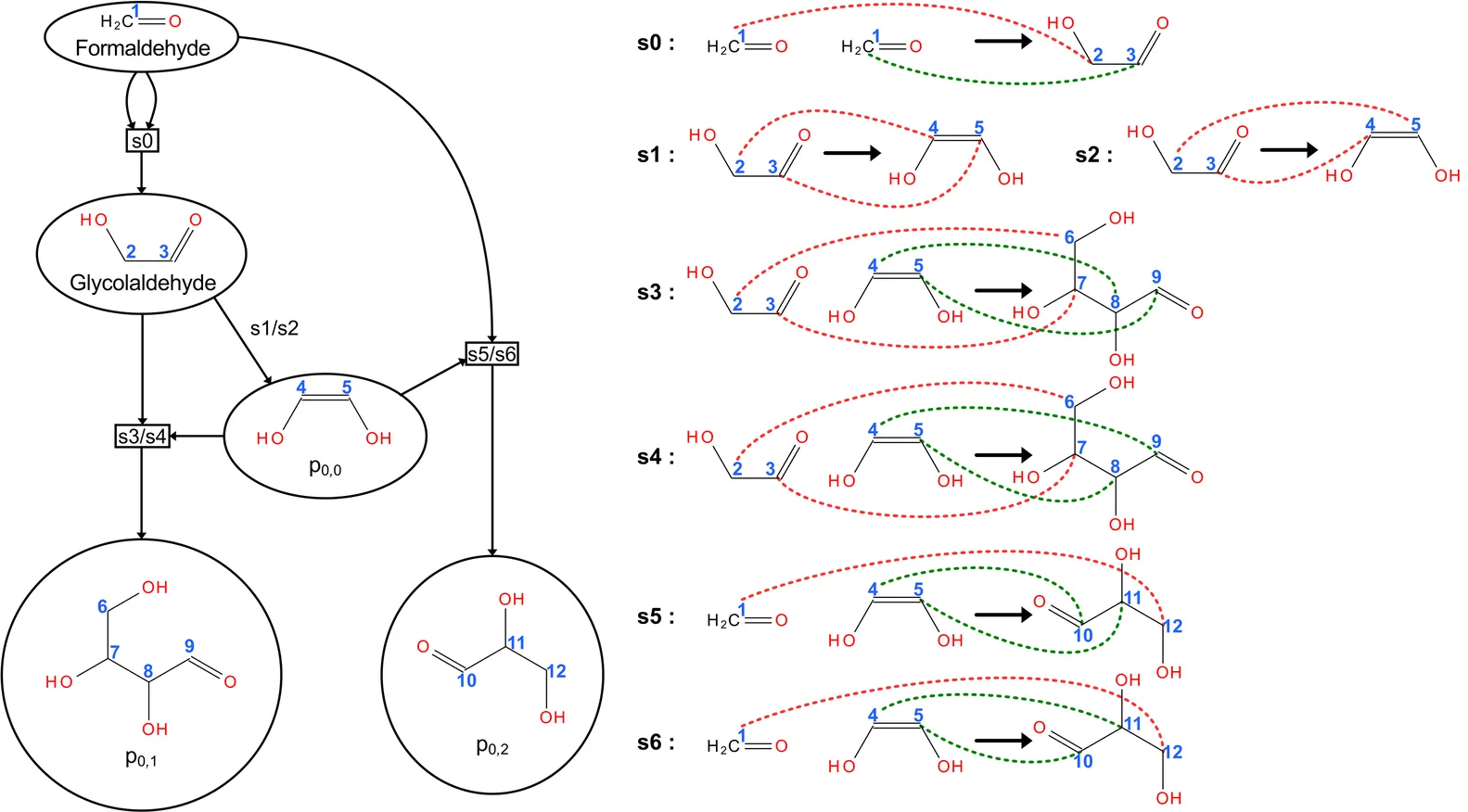
Atom tracing is essential for understanding the fate of labeled atoms in biochemical reaction networks, yet existing computational methods either simplify label correlations or suffer from combinatorial explosion. We introduce a saturation-based framework for enumerating labeling patterns that directly operates on atom-atom maps without requiring flux data or experimental measurements. The approach models reaction semantics using Kleisli morphisms in the powerset monad, allowing for compositional propagation of atom provenance through reaction networks. By iteratively saturating all possible educt combinations of reaction rules, the method exhaustively enumerates labeled molecular configurations, including multiplicities and reuse. Allowing arbitrary initial labeling patterns - including identical or distinct labels - the method expands only isotopomers reachable from these inputs, keeping the configuration space as small as necessary and avoids the full combinatorial growth characteristic of previous approaches. In principle, even every atom could carry a distinct identifier (e.g., tracing all carbon atoms individually), illustrating the generality of the framework beyond practical experimental limitations. The resulting template instance hypergraph captures the complete flow of atoms between compounds and supports projections tailored to experimental targets. Customizable labeling sets significantly reduce generated network sizes, providing efficient and exact atom traces focused on specific compounds or available isotopes. Applications to the tricarboxylic acid cycle, and glycolytic pathways demonstrate that the method fully automatically reproduces known labeling patterns and discovers steady-state labeling behavior. The framework offers a scalable, mechanistically transparent, and generalizable foundation for isotopomer modeling and experiment design.
2512.10708Dec 2025
View
Tracking large chemical reaction networks and rare events by neural networks
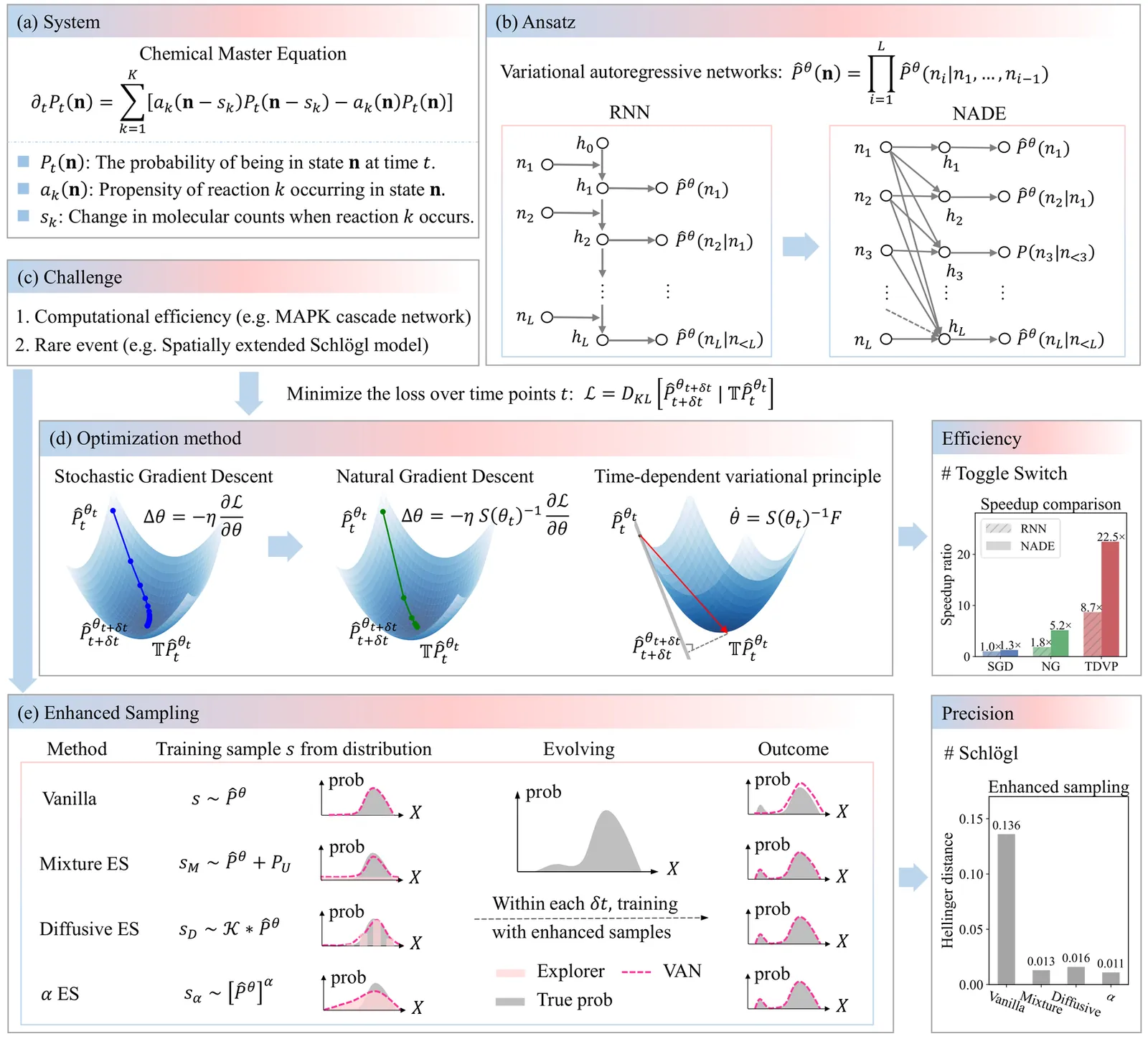
Chemical reaction networks are widely used to model stochastic dynamics in chemical kinetics, systems biology and epidemiology. Solving the chemical master equation that governs these systems poses a significant challenge due to the large state space exponentially growing with system sizes. The development of autoregressive neural networks offers a flexible framework for this problem; however, its efficiency is limited especially for high-dimensional systems and in scenarios with rare events. Here, we push the frontier of neural-network approach by exploiting faster optimizations such as natural gradient descent and time-dependent variational principle, achieving a 5- to 22-fold speedup, and by leveraging enhanced-sampling strategies to capture rare events. We demonstrate reduced computational cost and higher accuracy over the previous neural-network method in challenging reaction networks, including the mitogen-activated protein kinase (MAPK) cascade network, the hitherto largest biological network handled by the previous approaches of solving the chemical master equation. We further apply the approach to spatially extended reaction-diffusion systems, the Schlögl model with rare events, on two-dimensional lattices, beyond the recent tensor-network approach that handles one-dimensional lattices. The present approach thus enables efficient modeling of chemical reaction networks in general.
2512.10309Dec 2025
View
Interpretable Neural Approximation of Stochastic Reaction Dynamics with Guaranteed Reliability
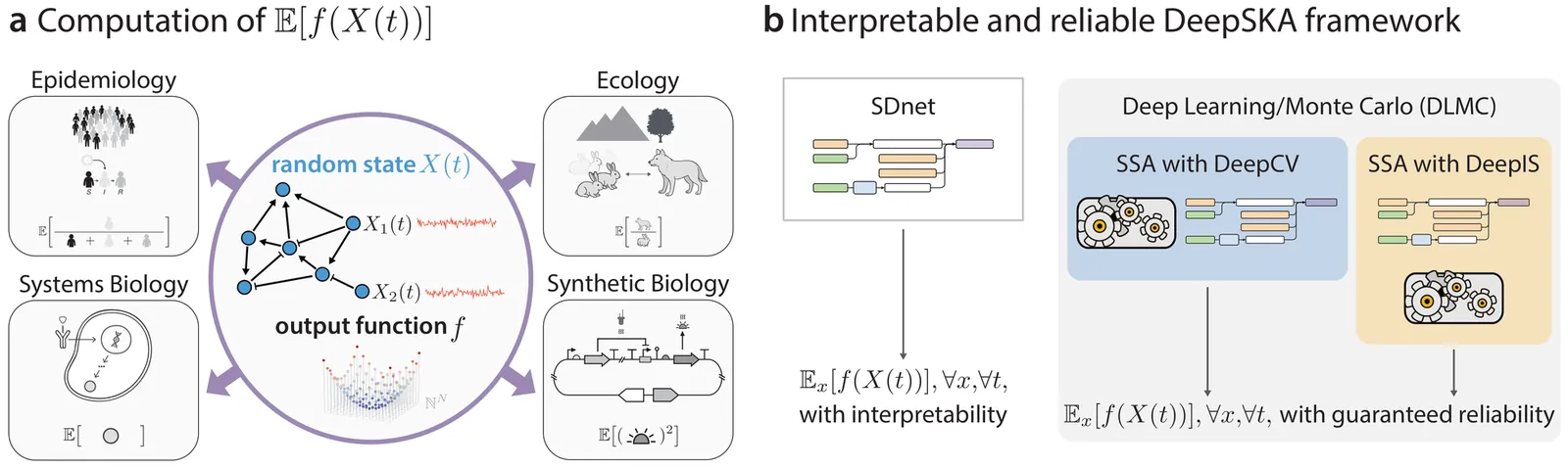
Stochastic Reaction Networks (SRNs) are a fundamental modeling framework for systems ranging from chemical kinetics and epidemiology to ecological and synthetic biological processes. A central computational challenge is the estimation of expected outputs across initial conditions and times, a task that is rarely solvable analytically and becomes computationally prohibitive with current methods such as Finite State Projection or the Stochastic Simulation Algorithm. Existing deep learning approaches offer empirical scalability, but provide neither interpretability nor reliability guarantees, limiting their use in scientific analysis and in applications where model outputs inform real-world decisions. Here we introduce DeepSKA, a neural framework that jointly achieves interpretability, guaranteed reliability, and substantial computational gains. DeepSKA yields mathematically transparent representations that generalise across states, times, and output functions, and it integrates this structure with a small number of stochastic simulations to produce unbiased, provably convergent, and dramatically lower-variance estimates than classical Monte Carlo. We demonstrate these capabilities across nine SRNs, including nonlinear and non-mass-action models with up to ten species, where DeepSKA delivers accurate predictions and orders-of-magnitude efficiency improvements. This interpretable and reliable neural framework offers a principled foundation for developing analogous methods for other Markovian systems, including stochastic differential equations.
2512.062941Dec 2025
View
Simulation and inference methods for non-Markovian stochastic biochemical reaction networks
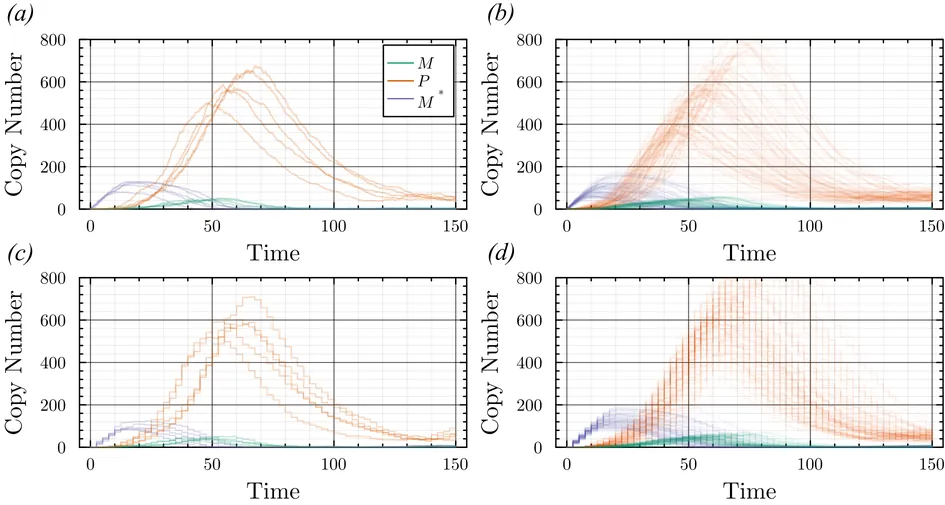
Stochastic models of biochemical reaction networks are widely used to capture intrinsic noise in cellular systems. The typical formulation of these models are based on Markov processes for which there is extensive research on efficient simulation and inference. However, there are biological processes, such as gene transcription and translation, that introduce history dependent dynamics requiring non-Markovian processes to accurately capture the stochastic dynamics of the system. This greater realism comes with additional computational challenges for simulation and parameter inference. We develop efficient stochastic simulation algorithms for well-mixed non-Markovian stochastic biochemical reaction networks with delays that depend on system state and time. Our methods generalize the next reaction method and $τ$-leaping method to support arbitrary inter-event time distributions while preserving computational scalability. We also introduce a coupling scheme to generate exact non-Markovian sample paths that are positively correlated to an approximate non-Markovian $τ$-leaping sample path. This enables substantial computational gains for Bayesian inference of model parameters though multifidelity simulation-based inference schemes. We demonstrate the effectiveness of our approach on a gene regulation model with delayed auto-inhibition, showing substantial gains in both simulation accuracy and inference efficiency of two orders of magnitude. These results extend the practical applicability of non-Markovian models in systems biology and beyond.
2512.02478Dec 2025
View
Hierarchical Molecular Language Models (HMLMs)
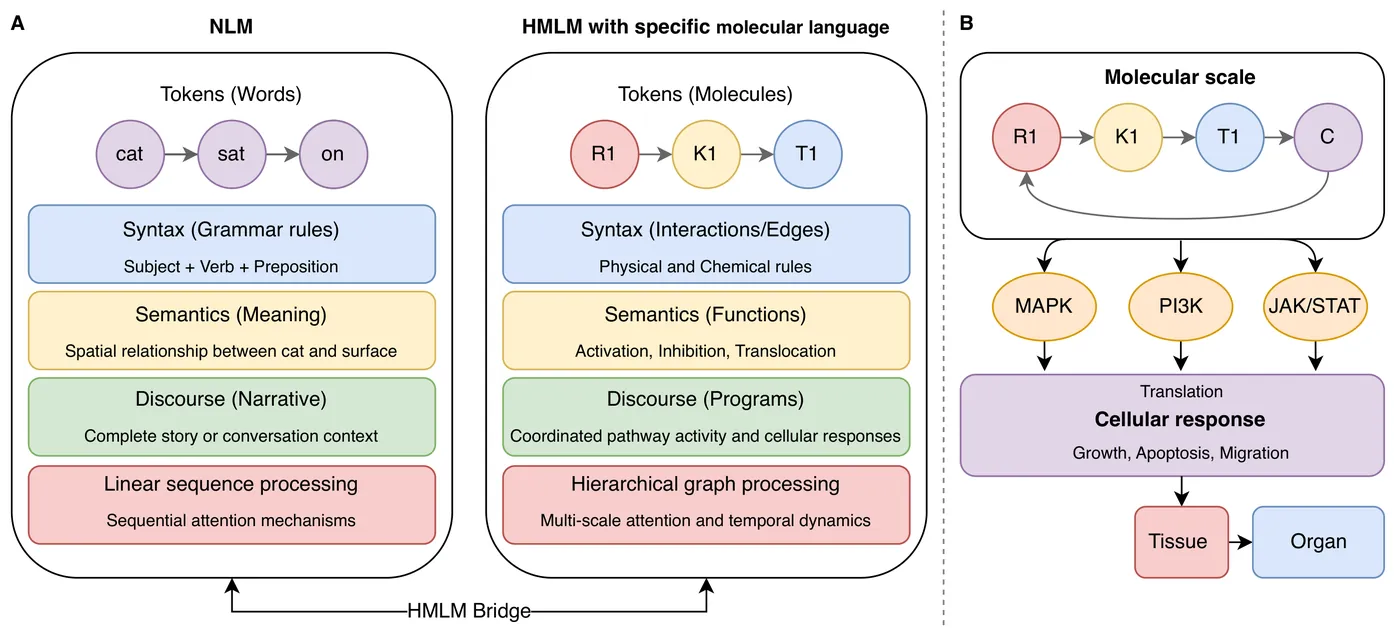
Artificial intelligence (AI) is reshaping computational and network biology by enabling new approaches to decode cellular communication networks. We introduce Hierarchical Molecular Language Models (HMLMs), a novel framework that models cellular signaling as a specialized molecular language, where signaling molecules function as tokens, protein interactions define syntax, and functional consequences constitute semantics. HMLMs employ a transformer-based architecture adapted to accommodate graph-structured signaling networks through information transducers, mathematical entities that capture how molecules receive, process, and transmit signals. The architecture integrates multi-modal data sources across molecular, pathway, and cellular scales through hierarchical attention mechanisms and scale-bridging operators that enable information flow across biological hierarchies. Applied to a complex network of cardiac fibroblast signaling, HMLMs outperformed traditional approaches in temporal dynamics prediction, particularly under sparse sampling conditions. Attention-based analysis revealed biologically meaningful crosstalk patterns, including previously uncharacterized interactions between signaling pathways. By bridging molecular mechanisms with cellular phenotypes through AI-driven molecular language representation, HMLMs establish a foundation for biology-oriented large language models (LLMs) that could be pre-trained on comprehensive pathway datasets and applied across diverse signaling systems and tissues, advancing precision medicine and therapeutic discovery.
2512.00696Nov 2025
View
A Spectral Koopman Approximation Framework for Stochastic Reaction Networks
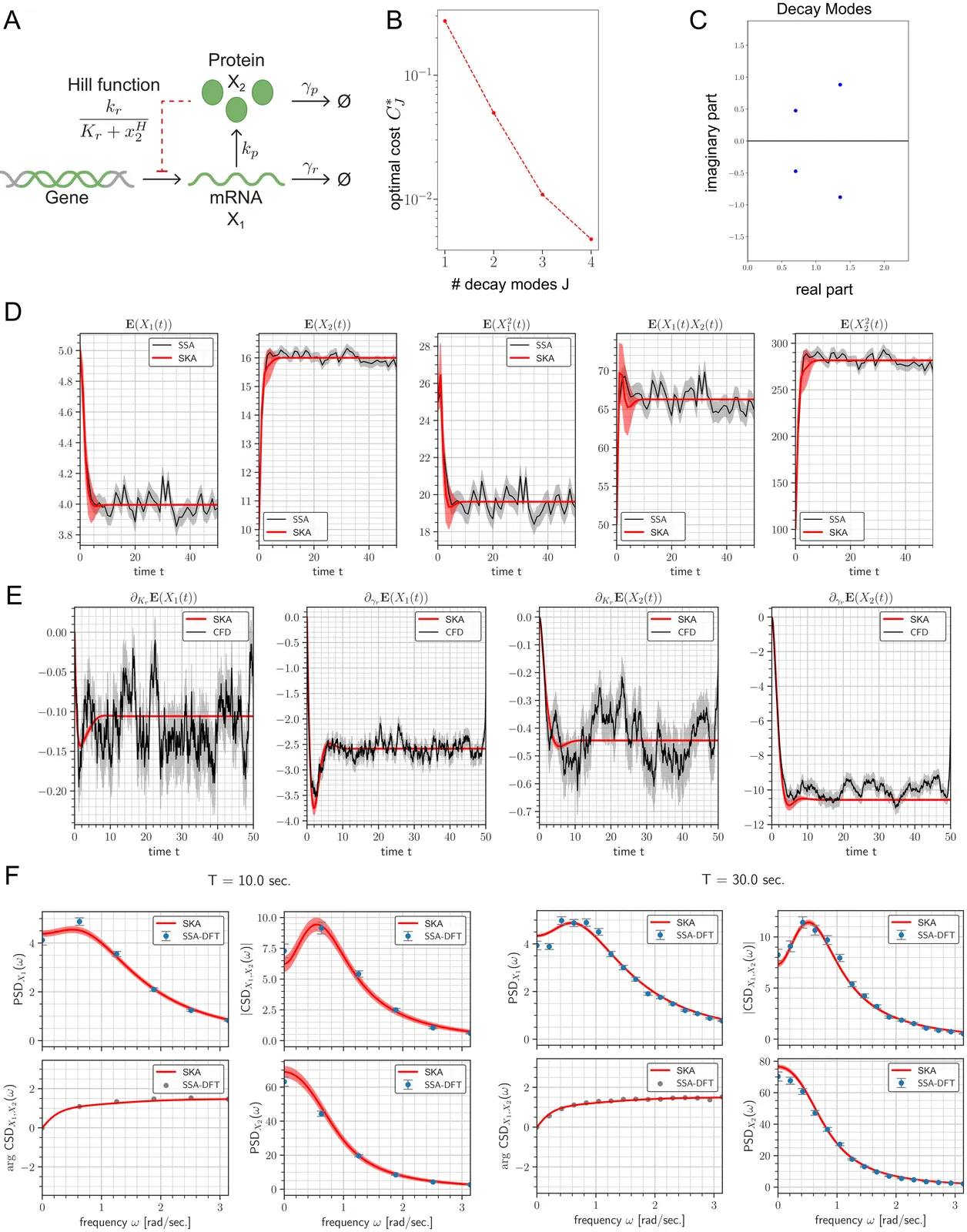
Stochastic reaction networks (SRNs) are a general class of continuous-time Markov jump processes used to model a wide range of systems, including biochemical dynamics in single cells, ecological and epidemiological populations, and queueing or communication networks. Yet analyzing their dynamics remains challenging because these processes are high-dimensional and their transient behavior can vary substantially across different initial molecular or population states. Here we introduce a spectral framework for the stochastic Koopman operator that provides a tractable, low-dimensional representation of SRN dynamics over continuous time, together with computable error estimates. By exploiting the compactness of the Koopman operator, we recover dominant spectral modes directly from simulated or experimental data, enabling efficient prediction of moments, event probabilities, and other summary statistics across all initial states. We further derive continuous-time parameter sensitivities and cross-spectral densities, offering new tools for probing noise structure and frequency-domain behavior. We demonstrate the approach on biologically relevant systems, including synthetic intracellular feedback controllers, stochastic oscillators, and inference of initial-state distributions from high-temporal-resolution flow cytometry. Together, these results establish spectral Koopman analysis as a powerful and general framework for studying stochastic dynamical systems across the biological, ecological, and computational sciences.
2511.231141Nov 2025
View
Enumeration of Autocatalytic Subsystems in Large Chemical Reaction Networks
Autocatalysis is an important feature of metabolic networks, contributing crucially to the self-maintenance of organisms. Autocatalytic subsystems of chemical reaction networks (CRNs) are characterized in terms of algebraic conditions on submatrices of the stoichiometric matrix. Here, we derive sufficient conditions for subgraphs supporting irreducible autocatalytic systems in the bipartite König representation of the CRN. On this basis, we develop an efficient algorithm to enumerate autocatalytic subnetworks and, as a special case, autocatalytic cores, i.e., minimal autocatalytic subnetworks, in full-size metabolic networks. The same algorithmic approach can also be used to determine autocatalytic cores only. As a showcase application, we provide a complete analysis of autocatalysis in the core metabolism of E. coli and enumerate irreducible autocatalytic subsystems of limited size in full-fledged metabolic networks of E. coli, human erythrocytes, and Methanosarcina barkeri (Archea). The mathematical and algorithmic results are accompanied by software enabling the routine analysis of autocatalysis in large CRNs.
2511.18883Nov 2025
View
Canalization as a stabilizing principle of gene regulatory networks: a discrete dynamical systems perspective
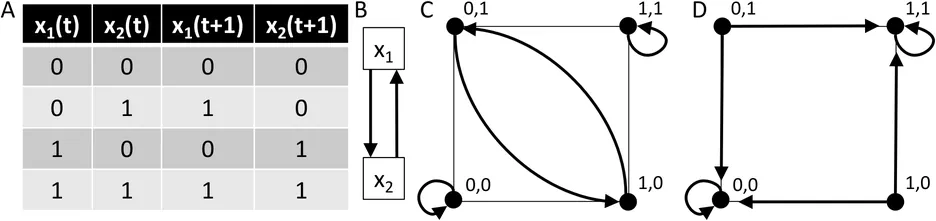
Gene regulatory networks exhibit remarkable stability, maintaining functional phenotypes despite genetic and environmental perturbations. Discrete dynamical models, such as Boolean networks, provide systems biologists with a tractable framework to explore the mathematical underpinnings of this robustness. A key mechanism conferring stability is canalization. This perspective synthesizes historical insights, formal definitions of canalization in discrete dynamical models, quantitative measures of stability, illustrative applications, and emerging challenges at the interface of theory and experiment.
2511.17905Nov 2025
View
BiRNe: Symbolic bifurcation analysis of reaction networks with Python
Computer algebra methods for analyzing reaction networks often rely on the assumption of mass-action kinetics, which transform the governing ODEs into polynomial systems amenable to techniques such as Gröbner basis computation and related algebraic tools. However, these methods face significant computational complexity, limiting their applicability to relatively small networks involving only a handful of species. In contrast, building on recent theoretical advances, we introduce here \textsc{BiRNe} (BIfurcations in Reaction NEtworks) Python module, which relies on a symbolic approach designed to detect bifurcations in larger reaction networks (up to 10-20 species, depending on the network's connectivity) equipped with parameter-rich kinetics. This class includes enzymatic kinetics such as Michaelis--Menten, ligand-binding kinetics like Hill functions, and generalized mass-action kinetics. For a given network, the current algorithm identifies all minimal autocatalytic subnetworks and fully characterizes the presence of bifurcations associated with zero eigenvalues, thus determining whether the network admits multistationarity. It also detects oscillatory bifurcations arising from positive-feedback structures, capturing a significant class of possible oscillations.
2511.14431Nov 2025
View
Biomolecular LQR under Partial Observation
This paper introduces a biomolecular Linear Quadratic Regulator (LQR) to investigate the design principles of gene regulatory networks. We show that for fundamental gene regulation network, the bio-controller derived from LQR theory precisely recapitulate natural network motifs, such as auto-regulation and incoherent feedforward loops. This emulation arises from a fundamental principle: the LQR cost function mathematically encodes environmental survival demands, which subsequently drives the selection of both network topology and biochemical parameters. Our work thus establishes a theoretical basis for interpreting biological circuit design, directly linking evolutionary pressures to observable regulatory structures.
2511.02418Nov 2025
View
ECMSim: A high-performance web simulation of cardiac ECM remodeling through integrated ODE-based signaling and diffusion
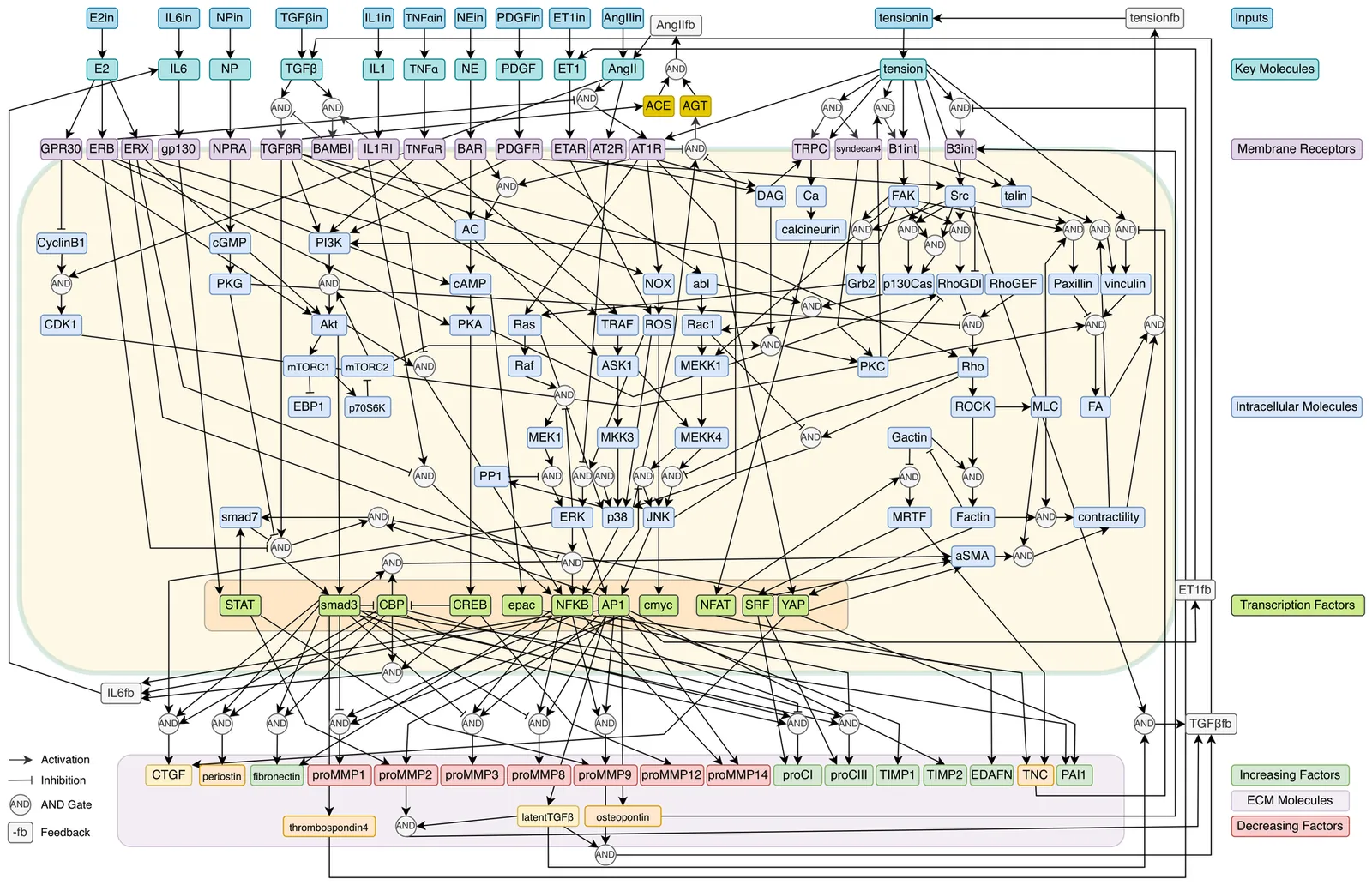
Extracellular matrix (ECM) remodeling is central to a wide variety of healthy and diseased tissue processes. Unfortunately, predicting ECM remodeling under various chemical and mechanical conditions has proven to be excessively challenging, due in part to its complex regulation by intracellular and extracellular molecular reaction networks that are spatially and temporally dynamic. We introduce ECMSim, which is a highly interactive, real-time, and web application designed to simulate heterogeneous matrix remodeling. The current model simulates cardiac scar tissue with configurable input conditions using a large-scale model of the cardiac fibroblast signaling network. Cardiac fibrosis is a major component of many forms of heart failure. ECMSim simulates over 1.3 million equations simultaneously in real time that include more than 125 species and more than 200 edges in each cell in a 100*100 spatial array (10,000 cells), which accounts for inputs, receptors, intracellular signaling cascades, ECM production, and feedback loops, as well as molecular diffusion. The algorithm is represented by a set of ordinary differential equations (ODEs) that are coupled with ECM molecular diffusion. The equations are solved on demand using compiled C++ and the WebAssembly standard. The platform includes brush-style cell selection to target a subset of cells with adjustable input molecule concentrations, parameter sliders to adjust parameters on demand, and multiple coupled real-time visualizations of network dynamics at multiple scales. Implementing ECMSim in standard web technologies enables a fully functional application that combines real-time simulation, visual interaction, and model editing. The software enables the investigation of pathological or experimental conditions, hypothetical scenarios, matrix remodeling, or the testing of the effects of an experimental drug(s) with a target receptor.
2510.125771Oct 2025
View
Adaptive Data-Knowledge Alignment in Genetic Perturbation Prediction
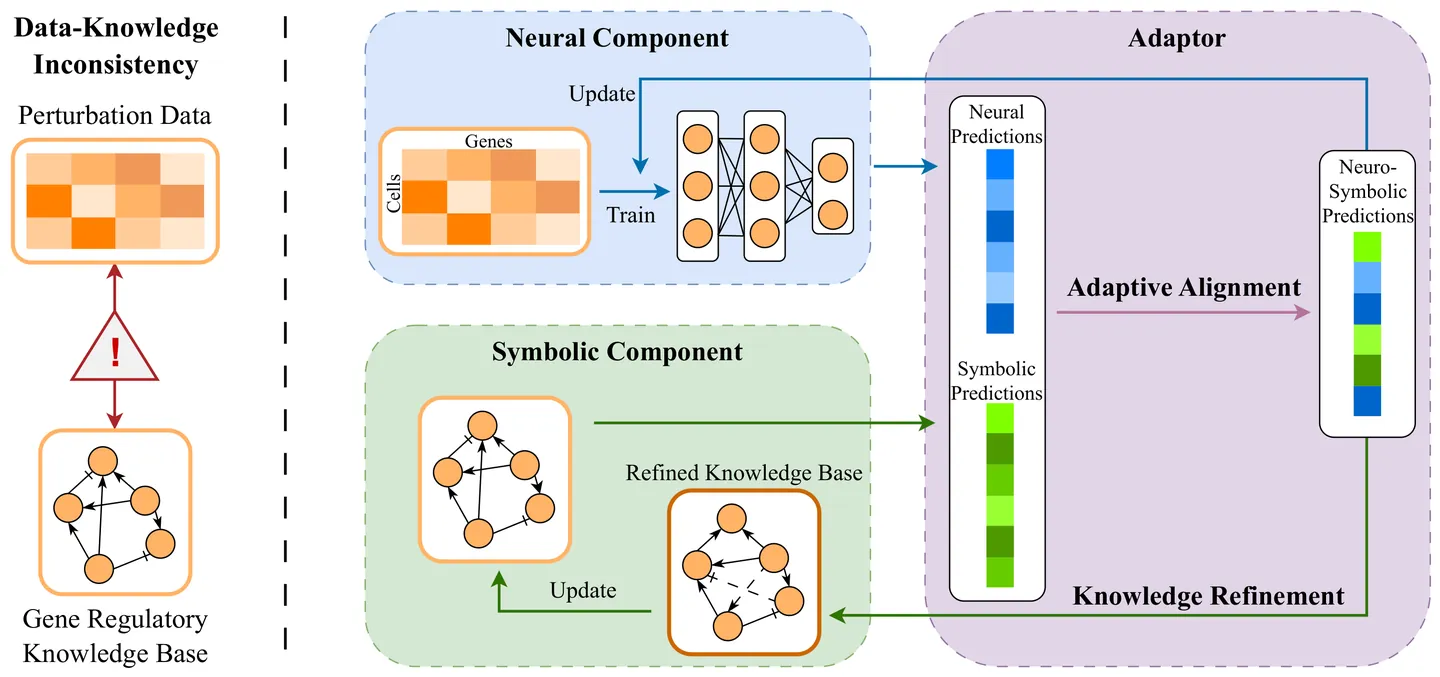
The transcriptional response to genetic perturbation reveals fundamental insights into complex cellular systems. While current approaches have made progress in predicting genetic perturbation responses, they provide limited biological understanding and cannot systematically refine existing knowledge. Overcoming these limitations requires an end-to-end integration of data-driven learning and existing knowledge. However, this integration is challenging due to inconsistencies between data and knowledge bases, such as noise, misannotation, and incompleteness. To address this challenge, we propose ALIGNED (Adaptive aLignment for Inconsistent Genetic kNowledgE and Data), a neuro-symbolic framework based on the Abductive Learning (ABL) paradigm. This end-to-end framework aligns neural and symbolic components and performs systematic knowledge refinement. We introduce a balanced consistency metric to evaluate the predictions' consistency against both data and knowledge. Our results show that ALIGNED outperforms state-of-the-art methods by achieving the highest balanced consistency, while also re-discovering biologically meaningful knowledge. Our work advances beyond existing methods to enable both the transparency and the evolution of mechanistic biological understanding.
2510.00512Oct 2025
View
Stoichiometric recipes for periodic oscillations in reaction networks
Oscillatory chemical reactions are functional components in a variety of biological contexts. In chemistry, the construction and identification of even rudimentary oscillators remain elusive and lack a general framework. Using parameter-rich kinetics - a methodology enabling the disentanglement of parametric dependencies from structural analysis - we investigate the stoichiometry of chemical oscillators. We introduce the concept of oscillatory cores: minimal subnetworks that guarantee the potential for oscillations in any reaction network containing them. These cores fall into two classes, depending on whether they involve positive or negative feedback. In particular, the latter class unveils a family of oscillators - yet to be synthesized - that require a minimum number of reaction steps to exhibit oscillations, a phenomenon we refer to as the principle of length. We identify several mechanisms through which catalysis promotes oscillations: (I) furnishing instability (e.g. autocatalysis), (II) lifting dependencies, (III) lowering length thresholds. Notwithstanding this mechanistic ubiquity, we show that oscillators can also be realized without employing any catalysis. Our results highlight branches of chemistry where oscillators are likely to arise by chance, suggest new strategies for their design, and point to novel classes of oscillators yet to be realized experimentally.
2508.152731Aug 2025
View
2507.09272Degeneracy of Zero-one Reaction Networks
Zero-one biochemical reaction networks are widely recognized for their importance in analyzing signal transduction and cellular decision-making processes. Degenerate networks reveal non-standard behaviors and mark the boundary where classical methods fail. Their analysis is key to understanding exceptional dynamical phenomena in biochemical systems. Therefore, we focus on investigating the degeneracy of zero-one reaction networks. It is known that one-dimensional zero-one networks cannot degenerate. In this work, we identify all degenerate two-dimensional zero-one reaction networks with up to three species by an efficient algorithm. By analyzing the structure of these networks, we arrive at the following conclusion: if a two-dimensional zero-one reaction network with three species is degenerate, then its steady-state system is equivalent to a binomial system.
2507.09272Jul 2025
View
Thermodynamic ranking of pathways in reaction networks
One of the puzzles left open by energetic analyses of irreversible stochastic processes is that boundary conditions that prevent the performance of work or the dissipation of heat make no contribution to an entropy-production budget; yet we see ubiquitously in both engineered and living systems that both transient and persistent energy costs are paid to create and maintain such boundaries. We wish to know whether there are inherent limits for the costs of such phenomena, and common units in which those can be traded off against more familiar costs measured in terms of heat dissipation. We give this problem a concrete framing in the context of CRNs, for the problem of extracting a topologically restricted pathway from a larger distributed network, through activation of some reactions and selective elimination of others. We define a thermodynamic cost function for pathways derived from large-deviation theory of stochastic CRNs, which decomposes into two components: an ongoing maintenance cost to sustain a NESS, and a restriction cost, quantifying the ongoing improbability of neutralizing reactions outside the specified pathway. Applying this formalism to detailed-balanced CRNs in the linear response regime, we make use of their formal equivalence to electrical circuits. We prove that the resistance of a CRN decreases as reactions are added that support the throughput current, and that the maintenance cost, the restriction cost, and the thermodynamic cost of nested pathways are bounded below by those of their hosting network. For small CRNs, we show how catalytic and inhibitory mechanisms can drastically alter pathway costs, enabling unfavorable pathways to become favorable and approach the cost of the hosting pathway. Our results provide insights into the thermodynamic principles governing open CRNs and offer a foundation for understanding the evolution of metabolic networks.
2506.234961Jun 2025
View
Functional classification of metabolic networks
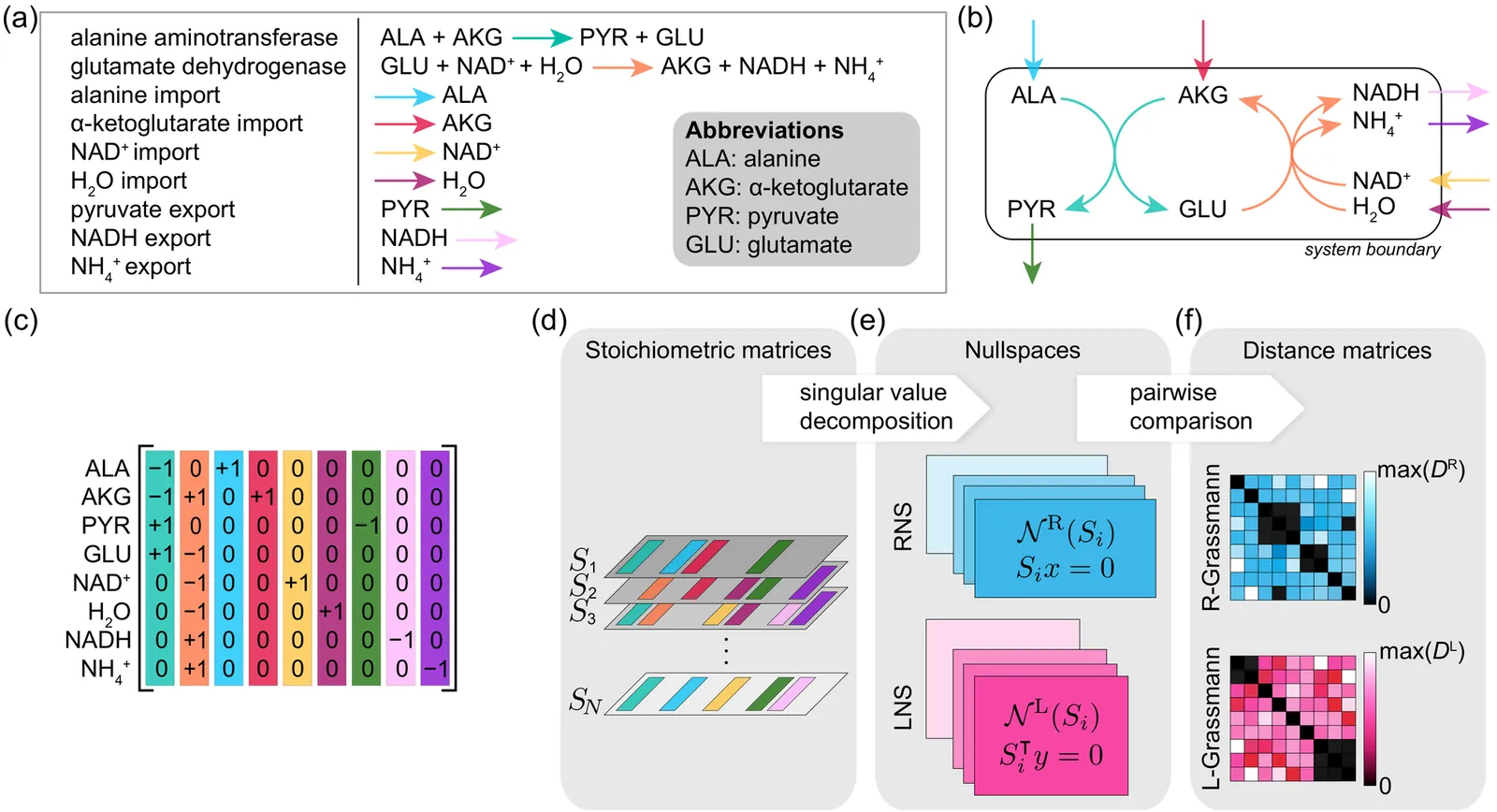
Chemical reaction networks underpin biological and physical phenomena across scales, from microbial interactions to planetary atmosphere dynamics. Bacterial communities exhibit complex competitive interactions for resources, human organs and tissues demonstrate specialized biochemical functions, and planetary atmospheres can display diverse organic and inorganic chemical processes. Despite their complexities, comparing these networks methodically remains a challenge due to the vast underlying degrees of freedom. In biological systems, comparative genomics has been pivotal in tracing evolutionary trajectories and classifying organisms via DNA sequences. However, purely genomic classifications often fail to capture functional roles within ecological systems. Metabolic changes driven by nutrient availability highlight the need for classification schemes that integrate metabolic information. Here we introduce and apply a computational framework for a classification scheme of organisms that compares matrix representations of chemical reaction networks using the Grassmann distance, corresponding to measuring distances between the nullspaces of stoichiometric matrices. Applying this framework to human gut microbiome data confirms that metabolic distances are distinct from phylogenetic distances, underscoring the limitations of genetic information in metabolic classification. Importantly, our analysis of metabolic distances reveals functional groups of organisms enriched or depleted in specific metabolic processes and shows robustness to metabolically silent genetic perturbations. The generalizability of metabolic Grassmann distances is illustrated by application to chemical reaction networks in human tissue and planetary atmospheres, highlighting its potential for advancing functional comparisons across diverse chemical reaction systems.
2503.144371Mar 2025
ViewPage 1 of 2
