Computational Finance
Computational methods for pricing and risk management, Monte Carlo, PDEs, numerical methods in finance.
Computational methods for pricing and risk management, Monte Carlo, PDEs, numerical methods in finance.
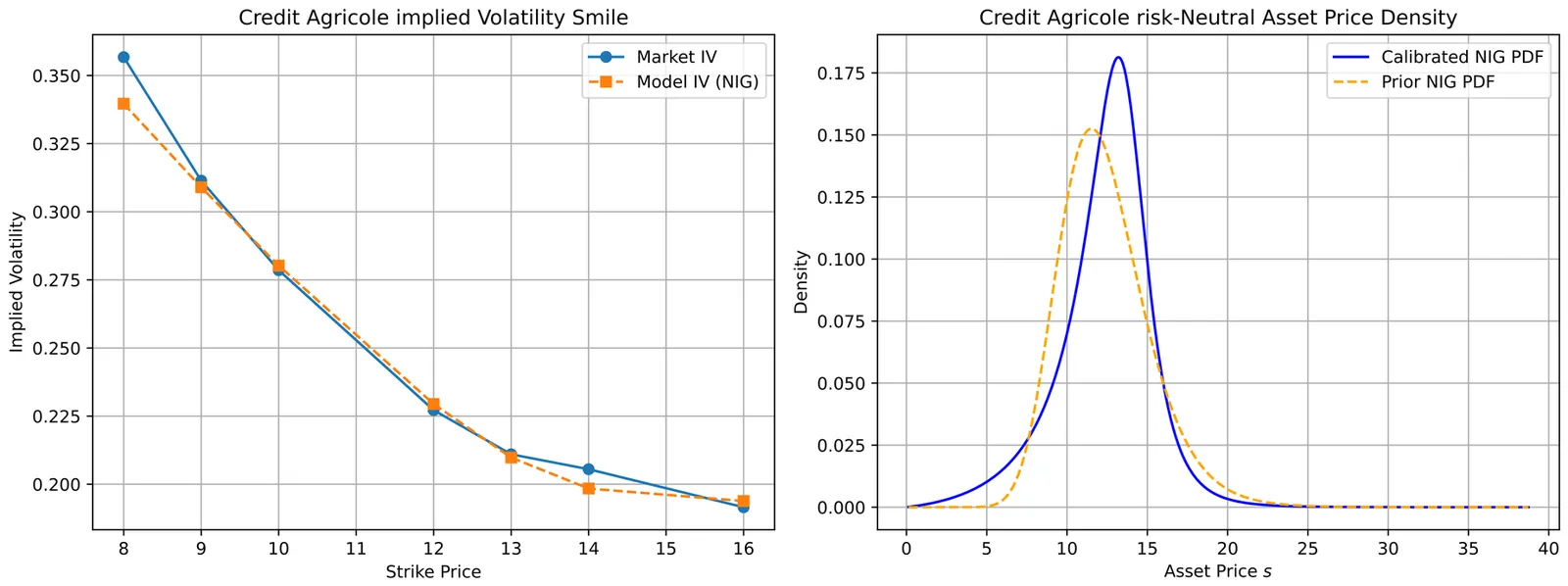
This work introduces an end-to-end framework for multi-asset option pricing that combines market-consistent risk-neutral density recovery with quantum-accelerated numerical integration. We first calibrate arbitrage-free marginal distributions from European option quotes using the Normal Inverse Gaussian (NIG) model, leveraging its analytical tractability and ability to capture skewness and fat tails. Marginals are coupled via a Gaussian copula to construct joint distributions. To address the computational bottleneck of the high-dimensional integration required to solve the option pricing formula, we employ Quantum Accelerated Monte Carlo (QAMC) techniques based on Quantum Amplitude Estimation (QAE), achieving quadratic convergence improvements over classical Monte Carlo (CMC) methods. Theoretical results establish accuracy bounds and query complexity for both marginal density estimation (via cosine-series expansions) and multidimensional pricing. Empirical tests on liquid equity entities (Credit Agricole, AXA, Michelin) confirm high calibration accuracy and demonstrate that QAMC requires 10-100 times fewer queries than classical methods for comparable precision. This study provides a practical route to integrate arbitrage-aware modelling with quantum computing, highlighting implications for scalability and future extensions to complex derivatives.
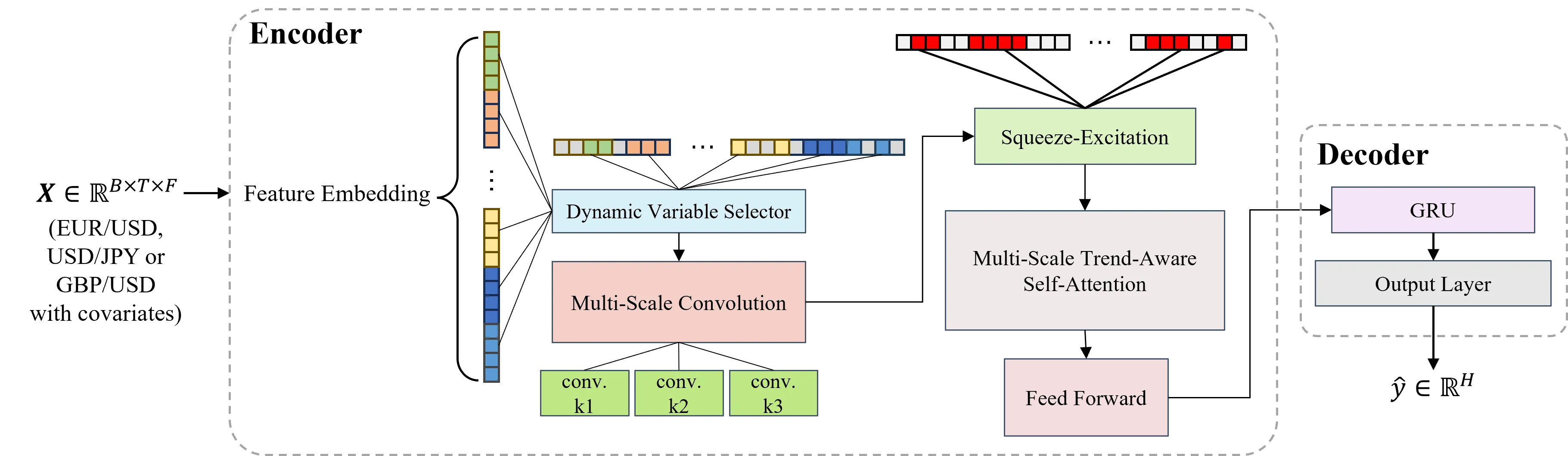
Accurately forecasting daily exchange rate returns represents a longstanding challenge in international finance, as the exchange rate returns are driven by a multitude of correlated market factors and exhibit high-frequency fluctuations. This paper proposes EXFormer, a novel Transformer-based architecture specifically designed for forecasting the daily exchange rate returns. We introduce a multi-scale trend-aware self-attention mechanism that employs parallel convolutional branches with differing receptive fields to align observations on the basis of local slopes, preserving long-range dependencies while remaining sensitive to regime shifts. A dynamic variable selector assigns time-varying importance weights to 28 exogenous covariates related to exchange rate returns, providing pre-hoc interpretability. An embedded squeeze-and-excitation block recalibrates channel responses to emphasize informative features and depress noise in the forecasting. Using the daily data for EUR/USD, USD/JPY, and GBP/USD, we conduct out-of-sample evaluations across five different sliding windows. EXFormer consistently outperforms the random walk and other baselines, improving directional accuracy by a statistically significant margin of up to 8.5--22.8%. In nearly one year of trading backtests, the model converts these gains into cumulative returns of 18%, 25%, and 18% for the three pairs, with Sharpe ratios exceeding 1.8. When conservative transaction costs and slippage are accounted for, EXFormer retains cumulative returns of 7%, 19%, and 9%, while other baselines achieve negative. The robustness checks further confirm the model's superiority under high-volatility and bear-market regimes. EXFormer furnishes both economically valuable forecasts and transparent, time-varying insights into the drivers of exchange rate dynamics for international investors, corporations, and central bank practitioners.
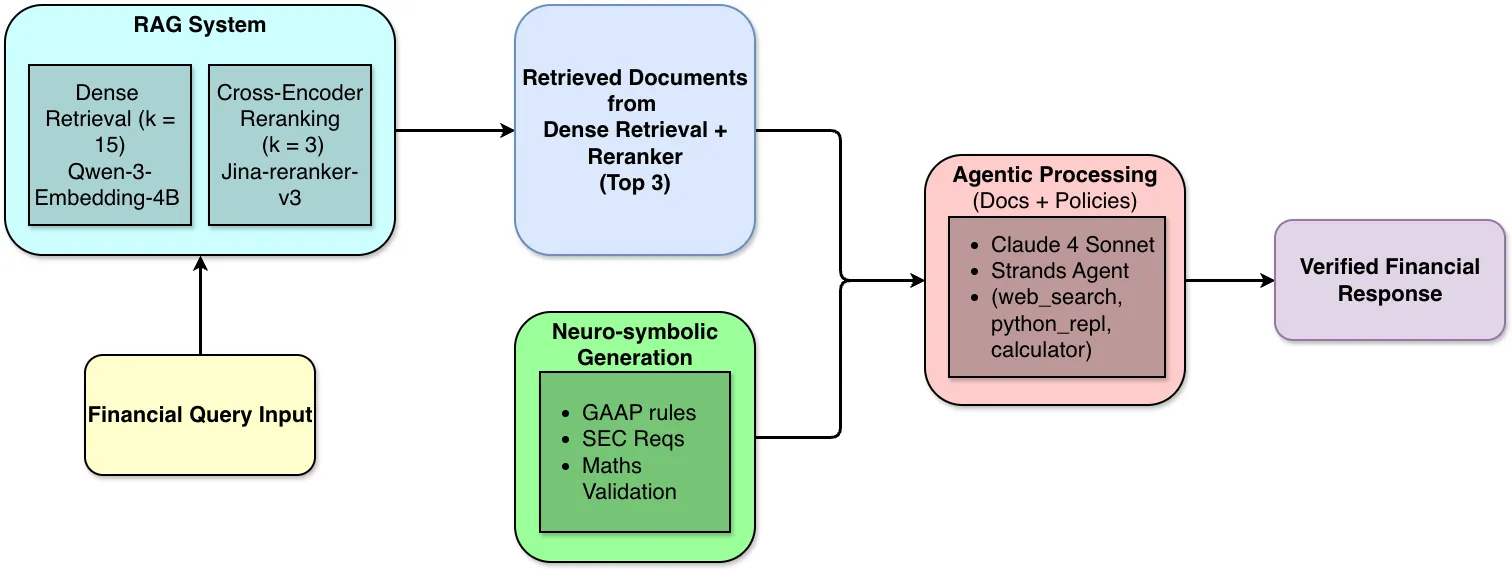
Financial AI systems suffer from a critical blind spot: while Retrieval-Augmented Generation (RAG) excels at finding relevant documents, language models still generate calculation errors and regulatory violations during reasoning, even with perfect retrieval. This paper introduces VERAFI (Verified Agentic Financial Intelligence), an agentic framework with neurosymbolic policy generation for verified financial intelligence. VERAFI combines state-of-the-art dense retrieval and cross-encoder reranking with financial tool-enabled agents and automated reasoning policies covering GAAP compliance, SEC requirements, and mathematical validation. Our comprehensive evaluation on FinanceBench demonstrates remarkable improvements: while traditional dense retrieval with reranking achieves only 52.4\% factual correctness, VERAFI's integrated approach reaches 94.7\%, an 81\% relative improvement. The neurosymbolic policy layer alone contributes a 4.3 percentage point gain over pure agentic processing, specifically targeting persistent mathematical and logical errors. By integrating financial domain expertise directly into the reasoning process, VERAFI offers a practical pathway toward trustworthy financial AI that meets the stringent accuracy demands of regulatory compliance, investment decisions, and risk management.
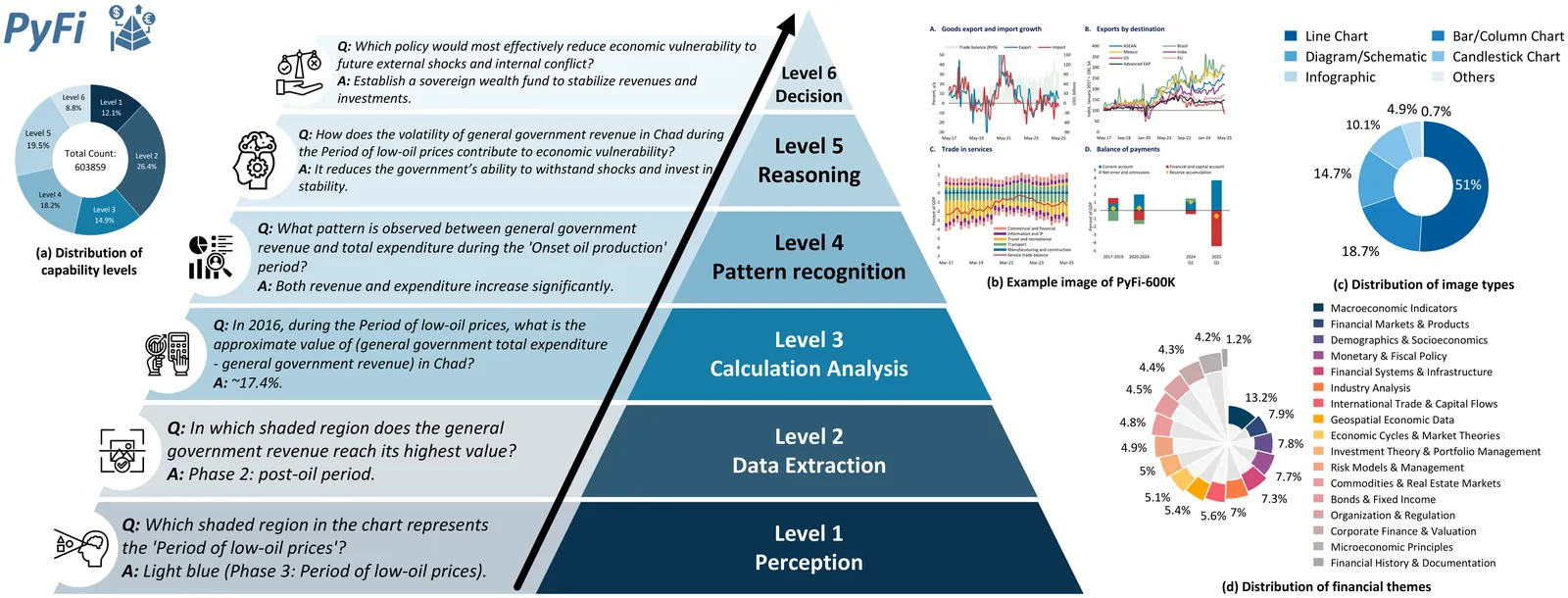
This paper proposes PyFi, a novel framework for pyramid-like financial image understanding that enables vision language models (VLMs) to reason through question chains in a progressive, simple-to-complex manner. At the core of PyFi is PyFi-600K, a dataset comprising 600K financial question-answer pairs organized into a reasoning pyramid: questions at the base require only basic perception, while those toward the apex demand increasing levels of capability in financial visual understanding and expertise. This data is scalable because it is synthesized without human annotations, using PyFi-adv, a multi-agent adversarial mechanism under the Monte Carlo Tree Search (MCTS) paradigm, in which, for each image, a challenger agent competes with a solver agent by generating question chains that progressively probe deeper capability levels in financial visual reasoning. Leveraging this dataset, we present fine-grained, hierarchical, and comprehensive evaluations of advanced VLMs in the financial domain. Moreover, fine-tuning Qwen2.5-VL-3B and Qwen2.5-VL-7B on the pyramid-structured question chains enables these models to answer complex financial questions by decomposing them into sub-questions with gradually increasing reasoning demands, yielding average accuracy improvements of 19.52% and 8.06%, respectively, on the dataset. All resources of code, dataset and models are available at: https://github.com/AgenticFinLab/PyFi .
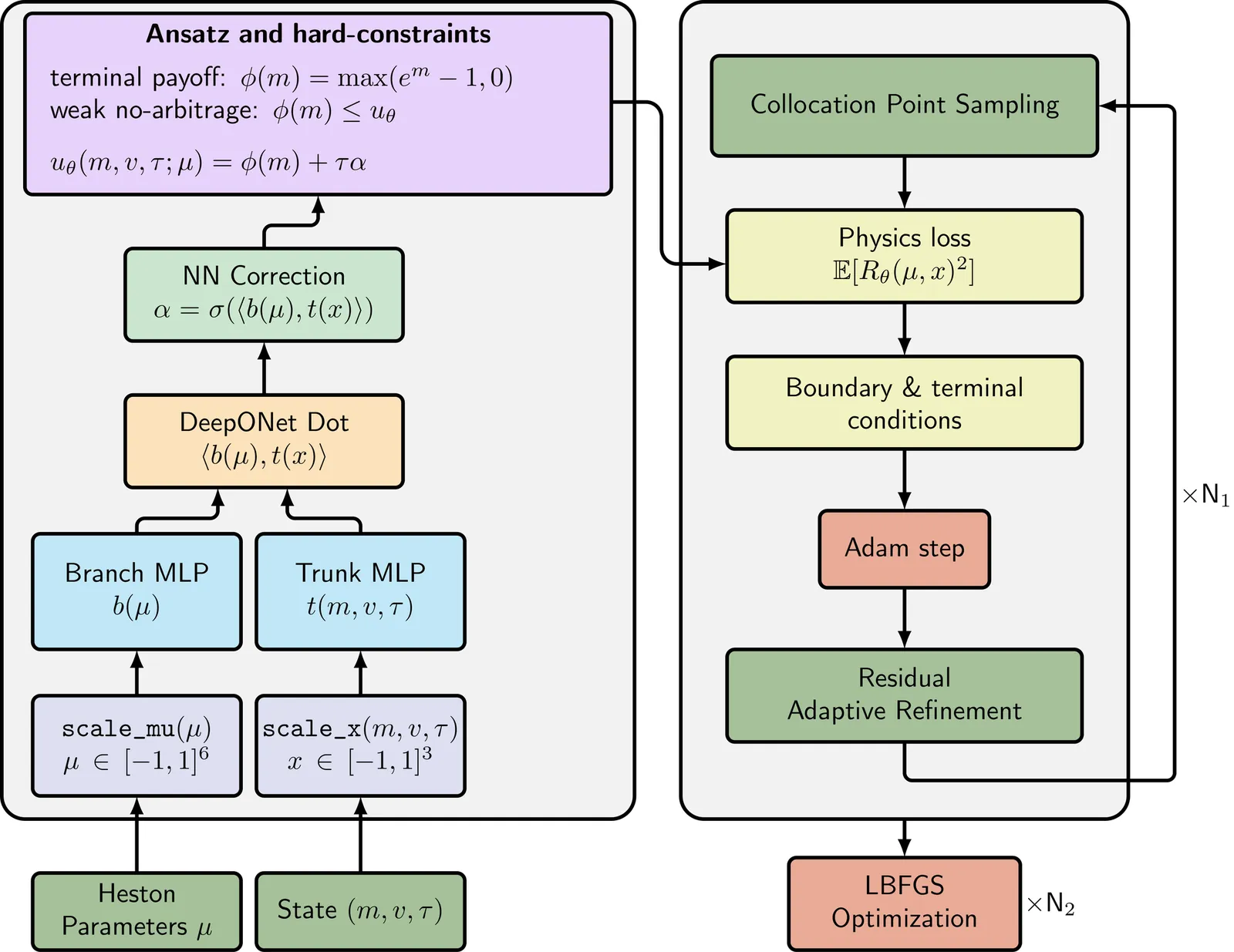
Real-time calibration of stochastic volatility models (SVMs) is computationally bottlenecked by the need to repeatedly solve coupled partial differential equations (PDEs). In this work, we propose DeepSVM, a physics-informed Deep Operator Network (PI-DeepONet) designed to learn the solution operator of the Heston model across its entire parameter space. Unlike standard data-driven deep learning (DL) approaches, DeepSVM requires no labelled training data. Rather, we employ a hard-constrained ansatz that enforces terminal payoffs and static no-arbitrage conditions by design. Furthermore, we use Residual-based Adaptive Refinement (RAR) to stabilize training in difficult regions subject to high gradients. Overall, DeepSVM achieves a final training loss of $10^{-5}$ and predicts highly accurate option prices across a range of typical market dynamics. While pricing accuracy is high, we find that the model's derivatives (Greeks) exhibit noise in the at-the-money (ATM) regime, highlighting the specific need for higher-order regularization in physics-informed operator learning.
We propose a convolution-FFT method for pricing European options under the Heston model that leverages a continuously differentiable representation of the joint characteristic function. Unlike existing Fourier-based methods that rely on branch-cut adjustments or empirically tuned damping parameters, our approach yields a stable integrand even under large frequency oscillations. Crucially, we derive fully analytical error bounds that quantify both truncation error and discretization error in terms of model parameters and grid settings. To the best of our knowledge, this is the first work to provide such explicit, closed-form error estimates for an FFT-based convolution method specialized to the Heston model. Numerical experiments confirm the theoretical rates and illustrate robust, high-accuracy option pricing at modest computational cost.
 2512.02745
2512.02745We study the truncation error of the COS method and give simple, verifiable conditions that guarantee convergence. In one dimension, COS is admissible when the density belongs to both L1 and L2 and has a finite weighted L2 moment of order strictly greater than one. We extend the result to multiple dimensions by requiring the moment order to exceed the dimension. These conditions enlarge the class of densities covered by previous analyses and include heavy-tailed distributions such as Student t with small degrees of freedom.
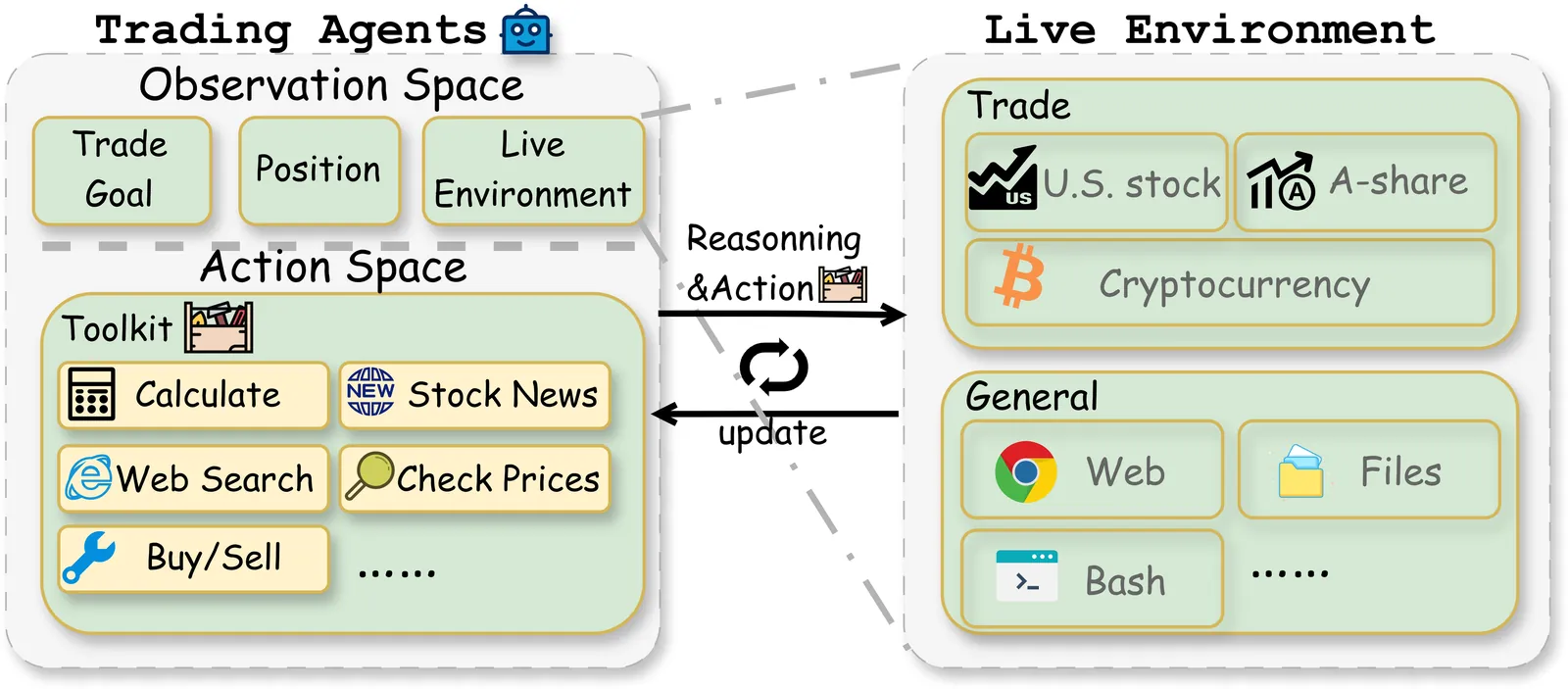
Large Language Models (LLMs) have demonstrated remarkable potential as autonomous agents, approaching human-expert performance through advanced reasoning and tool orchestration. However, decision-making in fully dynamic and live environments remains highly challenging, requiring real-time information integration and adaptive responses. While existing efforts have explored live evaluation mechanisms in structured tasks, a critical gap remains in systematic benchmarking for real-world applications, particularly in finance where stringent requirements exist for live strategic responsiveness. To address this gap, we introduce AI-Trader, the first fully-automated, live, and data-uncontaminated evaluation benchmark for LLM agents in financial decision-making. AI-Trader spans three major financial markets: U.S. stocks, A-shares, and cryptocurrencies, with multiple trading granularities to simulate live financial environments. Our benchmark implements a revolutionary fully autonomous minimal information paradigm where agents receive only essential context and must independently search, verify, and synthesize live market information without human intervention. We evaluate six mainstream LLMs across three markets and multiple trading frequencies. Our analysis reveals striking findings: general intelligence does not automatically translate to effective trading capability, with most agents exhibiting poor returns and weak risk management. We demonstrate that risk control capability determines cross-market robustness, and that AI trading strategies achieve excess returns more readily in highly liquid markets than policy-driven environments. These findings expose critical limitations in current autonomous agents and provide clear directions for future improvements. The code and evaluation data are open-sourced to foster community research: https://github.com/HKUDS/AI-Trader.
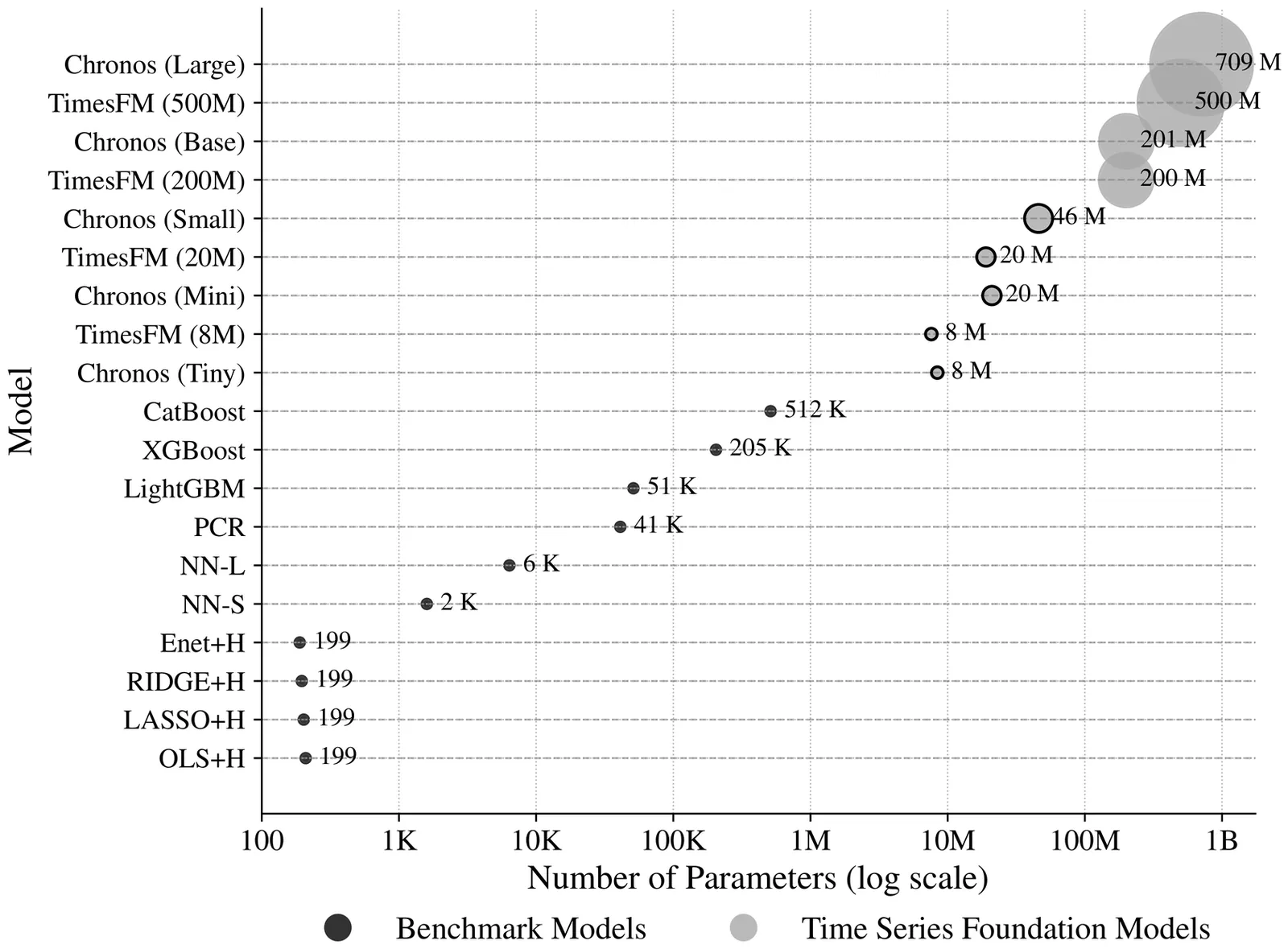
Financial time series forecasting is central to trading, portfolio optimization, and risk management, yet it remains challenging due to noisy, non-stationary, and heterogeneous data. Recent advances in time series foundation models (TSFMs), inspired by large language models, offer a new paradigm for learning generalizable temporal representations from large and diverse datasets. This paper presents the first comprehensive empirical study of TSFMs in global financial markets. Using a large-scale dataset of daily excess returns across diverse markets, we evaluate zero-shot inference, fine-tuning, and pre-training from scratch against strong benchmark models. We find that off-the-shelf pre-trained TSFMs perform poorly in zero-shot and fine-tuning settings, whereas models pre-trained from scratch on financial data achieve substantial forecasting and economic improvements, underscoring the value of domain-specific adaptation. Increasing the dataset size, incorporating synthetic data augmentation, and applying hyperparameter tuning further enhance performance.
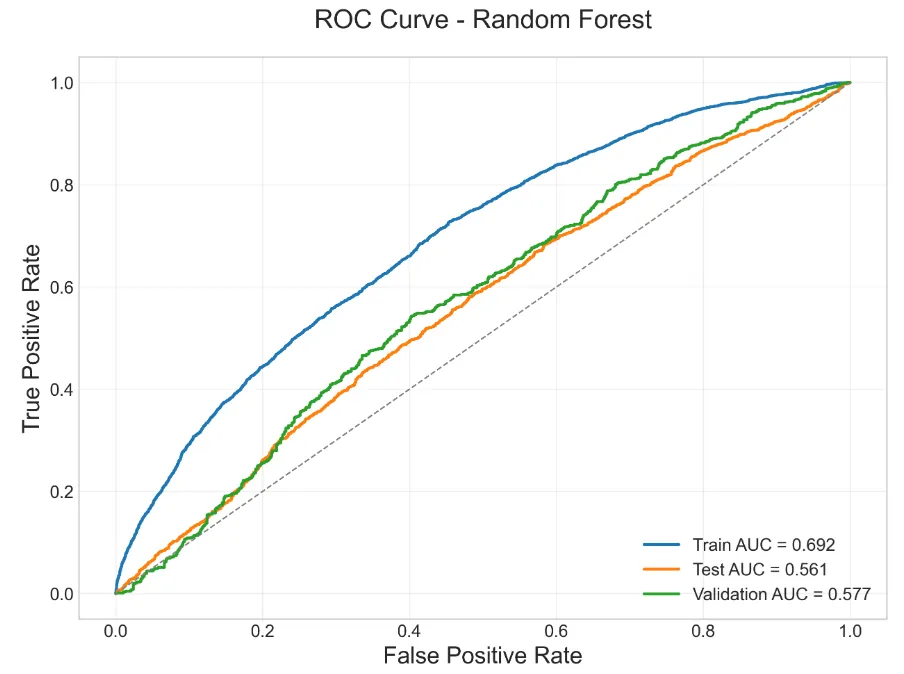
The aim of this paper is the analysis and selection of stock trading systems that combine different models with data of different nature, such as financial and microeconomic information. Specifically, based on previous work by the authors and applying advanced techniques of Machine Learning and Deep Learning, our objective is to formulate trading algorithms for the stock market with empirically tested statistical advantages, thus improving results published in the literature. Our approach integrates Long Short-Term Memory (LSTM) networks with algorithms based on decision trees, such as Random Forest and Gradient Boosting. While the former analyze price patterns of financial assets, the latter are fed with economic data of companies. Numerical simulations of algorithmic trading with data from international companies and 10-weekday predictions confirm that an approach based on both fundamental and technical variables can outperform the usual approaches, which do not combine those two types of variables. In doing so, Random Forest turned out to be the best performer among the decision trees. We also discuss how the prediction performance of such a hybrid approach can be boosted by selecting the technical variables.
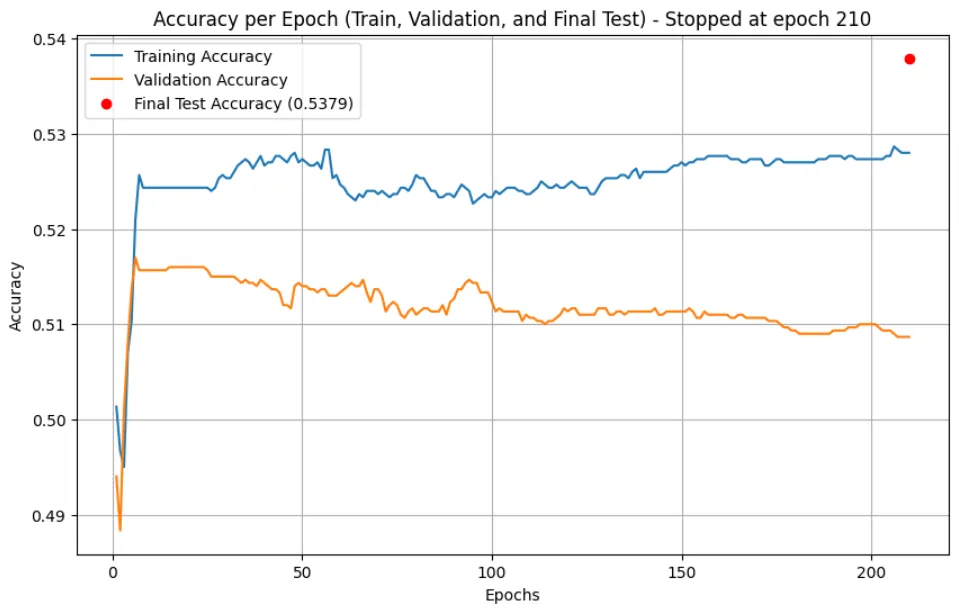
Binary options trading is often marketed as a field where predictive models can generate consistent profits. However, the inherent randomness and stochastic nature of binary options make price movements highly unpredictable, posing significant challenges for any forecasting approach. This study demonstrates that machine learning algorithms struggle to outperform a simple baseline in predicting binary options movements. Using a dataset of EUR/USD currency pairs from 2021 to 2023, we tested multiple models, including Random Forest, Logistic Regression, Gradient Boosting, and k-Nearest Neighbors (kNN), both before and after hyperparameter optimization. Furthermore, several neural network architectures, including Multi-Layer Perceptrons (MLP) and a Long Short-Term Memory (LSTM) network, were evaluated under different training conditions. Despite these exhaustive efforts, none of the models surpassed the ZeroR baseline accuracy, highlighting the inherent randomness of binary options. These findings reinforce the notion that binary options lack predictable patterns, making them unsuitable for machine learning-based forecasting.

This paper proposes a reinforcement learning--based framework for cryptocurrency portfolio management using the Soft Actor--Critic (SAC) and Deep Deterministic Policy Gradient (DDPG) algorithms. Traditional portfolio optimization methods often struggle to adapt to the highly volatile and nonlinear dynamics of cryptocurrency markets. To address this, we design an agent that learns continuous trading actions directly from historical market data through interaction with a simulated trading environment. The agent optimizes portfolio weights to maximize cumulative returns while minimizing downside risk and transaction costs. Experimental evaluations on multiple cryptocurrencies demonstrate that the SAC and DDPG agents outperform baseline strategies such as equal-weighted and mean--variance portfolios. The SAC algorithm, with its entropy-regularized objective, shows greater stability and robustness in noisy market conditions compared to DDPG. These results highlight the potential of deep reinforcement learning for adaptive and data-driven portfolio management in cryptocurrency markets.
 2511.04361
2511.04361Energy markets exhibit complex causal relationships between weather patterns, generation technologies, and price formation, with regime changes occurring continuously rather than at discrete break points. Current approaches model electricity prices without explicit causal interpretation or counterfactual reasoning capabilities. We introduce Augmented Time Series Causal Models (ATSCM) for energy markets, extending counterfactual reasoning frameworks to multivariate temporal data with learned causal structure. Our approach models energy systems through interpretable factors (weather, generation mix, demand patterns), rich grid dynamics, and observable market variables. We integrate neural causal discovery to learn time-varying causal graphs without requiring ground truth DAGs. Applied to real-world electricity price data, ATSCM enables novel counterfactual queries such as "What would prices be under different renewable generation scenarios?".
 2511.02469
2511.02469Accurately forecasting central bank policy decisions, particularly those of the Federal Open Market Committee(FOMC) has become increasingly important amid heightened economic uncertainty. While prior studies have used monetary policy texts to predict rate changes, most rely on static classification models that overlook the deliberative nature of policymaking. This study proposes a novel framework that structurally imitates the FOMC's collective decision-making process by modeling multiple large language models(LLMs) as interacting agents. Each agent begins with a distinct initial belief and produces a prediction based on both qualitative policy texts and quantitative macroeconomic indicators. Through iterative rounds, agents revise their predictions by observing the outputs of others, simulating deliberation and consensus formation. To enhance interpretability, we introduce a latent variable representing each agent's underlying belief(e.g., hawkish or dovish), and we theoretically demonstrate how this belief mediates the perception of input information and interaction dynamics. Empirical results show that this debate-based approach significantly outperforms standard LLMs-based baselines in prediction accuracy. Furthermore, the explicit modeling of beliefs provides insights into how individual perspectives and social influence shape collective policy forecasts.
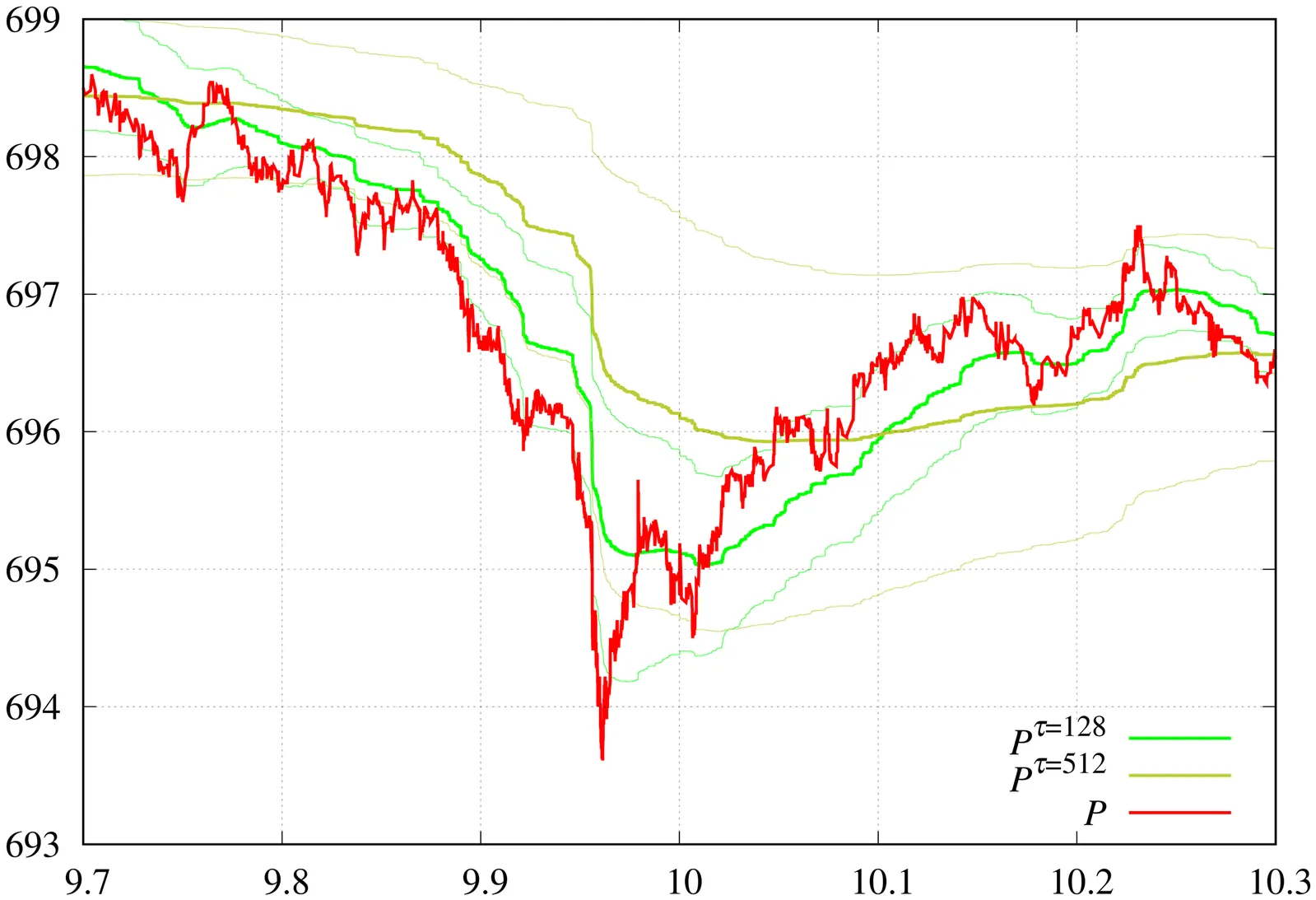
In this work, we demonstrate experimentally that the execution flow, $I = dV/dt$, is the fundamental driving force of market dynamics. We develop a numerical framework to calculate execution flow from sampled moments using the Radon-Nikodym derivative. A notable feature of this approach is its ability to automatically determine thresholds that can serve as actionable triggers. The technique also determines the characteristic time scale directly from the corresponding eigenproblem. The methodology has been validated on actual market data to support these findings. Additionally, we introduce a framework based on the Christoffel function spectrum, which is invariant under arbitrary non-degenerate linear transformations of input attributes and offers an alternative to traditional principal component analysis (PCA), which is limited to unitary invariance.
 2510.26217
2510.26217We address finance-native collateral optimization under ISDA Credit Support Annexes (CSAs), where integer lots, Schedule A haircuts, RA/MTA gating, and issuer/currency/class caps create rugged, legally bounded search spaces. We introduce a certifiable hybrid pipeline purpose-built for this domain: (i) an evidence-gated LLM that extracts CSA terms to a normalized JSON (abstain-by-default, span-cited); (ii) a quantum-inspired explorer that interleaves simulated annealing with micro higher order QAOA (HO-QAOA) on binding sub-QUBOs (subset size n <= 16, order k <= 4) to coordinate multi-asset moves across caps and RA-induced discreteness; (iii) a weighted risk-aware objective (Movement, CVaR, funding-priced overshoot) with an explicit coverage window U <= Reff+B; and (iv) CP-SAT as single arbiter to certify feasibility and gaps, including a U-cap pre-check that reports the minimal feasible buffer B*. Encoding caps/rounding as higher-order terms lets HO-QAOA target the domain couplings that defeat local swaps. On government bond datasets and multi-CSA inputs, the hybrid improves a strong classical baseline (BL-3) by 9.1%, 9.6%, and 10.7% across representative harnesses, delivering better cost-movement-tail frontiers under governance settings. We release governance grade artifacts-span citations, valuation matrix audit, weight provenance, QUBO manifests, and CP-SAT traces-to make results auditable and reproducible.
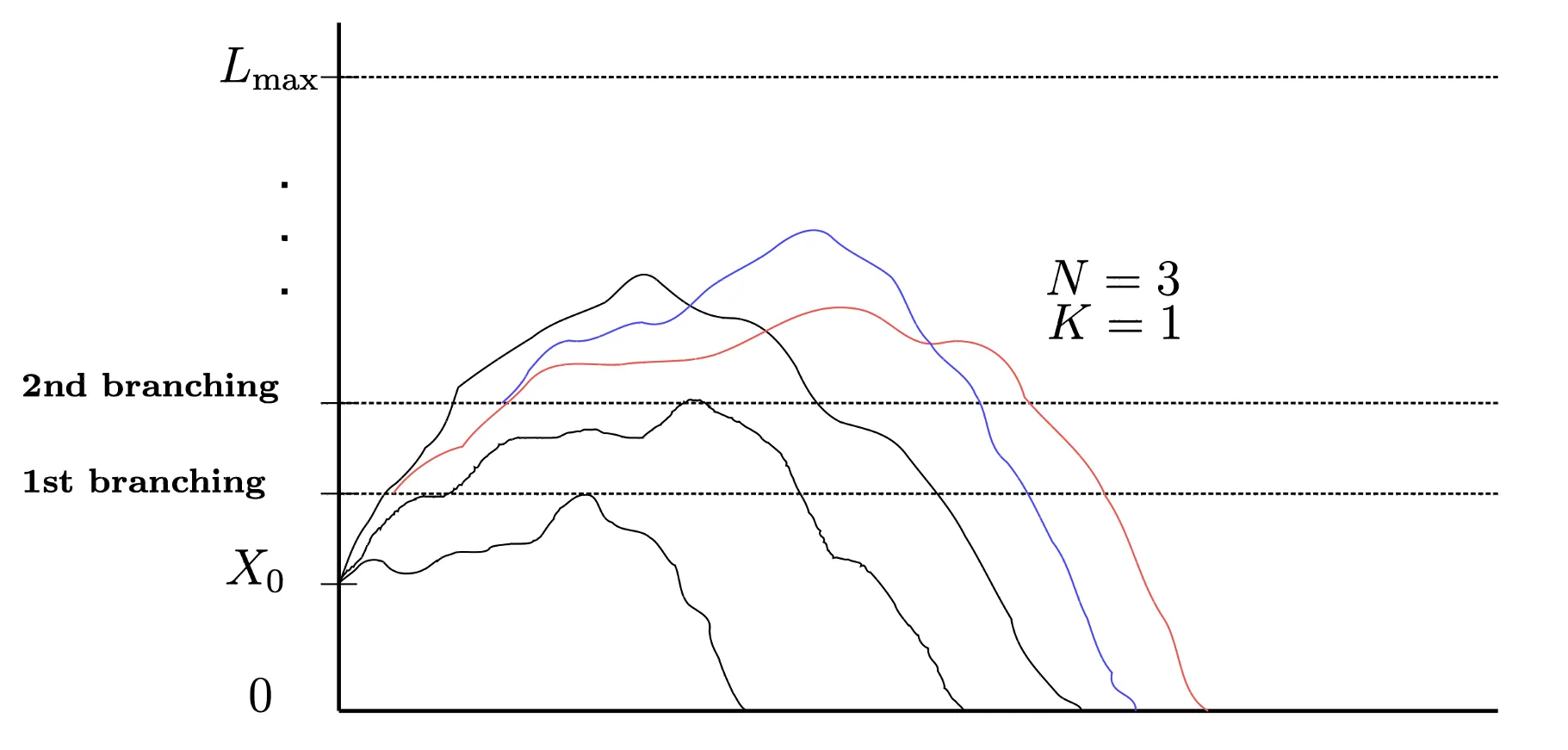
This work investigates the computational burden of pricing binary options in rare event regimes and introduces an adaptation of the adaptive multilevel splitting (AMS) method for financial derivatives. Standard Monte Carlo becomes inefficient for deep out-of-the-money binaries due to discontinuous payoffs and extremely small exercise probabilities, requiring prohibitively large sample sizes for accurate estimation. The proposed AMS framework reformulates the rare-event problem as a sequence of conditional events and is applied under both Black-Scholes and Heston dynamics. Numerical experiments cover European, Asian, and up-and-in barrier digital options, together with a multidimensional digital payoff designed as a stress test. Across all contracts, AMS achieves substantial gains, reaching up to 200-fold improvements over standard Monte Carlo, while preserving unbiasedness and showing robust performance with respect to the choice of importance function. To the best of our knowledge, this is the first application of AMS to derivative pricing. An open-source Rcpp implementation is provided, supporting multiple discretisation schemes and alternative importance functions.

We present an uncertainty-aware, physics-informed neural network (PINN) for option pricing that solves the Black--Scholes (BS) partial differential equation (PDE) as a mesh-free, global surrogate over $(S,t)$. The model embeds the BS operator and boundary/terminal conditions in a residual-based objective and requires no labeled prices. For American options, early exercise is handled via an obstacle-style relaxation while retaining the BS residual in the continuation region. To quantify \emph{epistemic} uncertainty, we introduce an anchored-ensemble fine-tuning stage (AT--PINN) that regularizes each model toward a sampled anchor and yields prediction bands alongside point estimates. On European calls/puts, the approach attains low errors (e.g., MAE $\sim 5\times10^{-2}$, RMSE $\sim 7\times10^{-2}$, explained variance $\approx 0.999$ in representative settings) and tracks ground truth closely across strikes and maturities. For American puts, the method remains accurate (MAE/RMSE on the order of $10^{-1}$ with EV $\approx 0.999$) and does not exhibit the error accumulation associated with time-marching schemes. Against data-driven baselines (ANN, RNN) and a Kolmogorov--Arnold FINN variant (KAN), our PINN matches or outperforms on accuracy while training more stably; anchored ensembles provide uncertainty bands that align with observed error scales. We discuss design choices (loss balancing, sampling near the payoff kink), limitations, and extensions to higher-dimensional BS settings and alternative dynamics.
 2510.22685
2510.22685The recent application of deep learning models to financial trading has heightened the need for high fidelity financial time series data. This synthetic data can be used to supplement historical data to train large trading models. The state-of-the-art models for the generative application often rely on huge amounts of historical data and large, complicated models. These models range from autoregressive and diffusion-based models through to architecturally simpler models such as the temporal-attention bilinear layer. Agent-based approaches to modelling limit order book dynamics can also recreate trading activity through mechanistic models of trader behaviours. In this work, we demonstrate how a popular agent-based framework for simulating intraday trading activity, the Chiarella model, can be combined with one of the most performant deep learning models for forecasting multi-variate time series, the TABL model. This forecasting model is coupled to a simulation of a matching engine with a novel method for simulating deleted order flow. Our simulator gives us the ability to test the generative abilities of the forecasting model using stylised facts. Our results show that this methodology generates realistic price dynamics however, when analysing deeper, parts of the markets microstructure are not accurately recreated, highlighting the necessity for including more sophisticated agent behaviors into the modeling framework to help account for tail events.
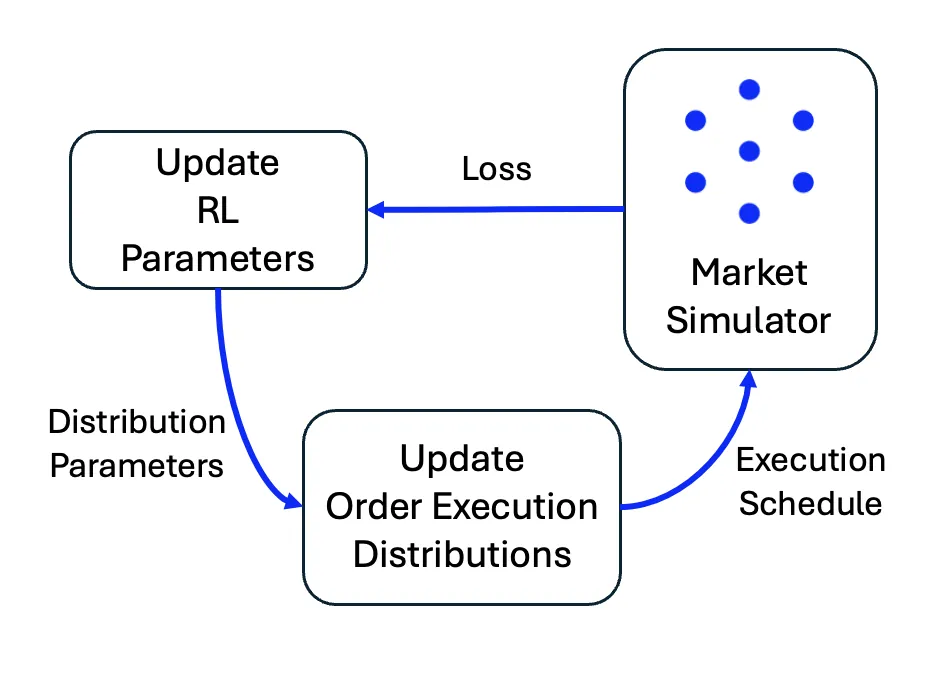
Execution algorithms are vital to modern trading, they enable market participants to execute large orders while minimising market impact and transaction costs. As these algorithms grow more sophisticated, optimising them becomes increasingly challenging. In this work, we present a reinforcement learning (RL) framework for discovering optimal execution strategies, evaluated within a reactive agent-based market simulator. This simulator creates reactive order flow and allows us to decompose slippage into its constituent components: market impact and execution risk. We assess the RL agent's performance using the efficient frontier based on work by Almgren and Chriss, measuring its ability to balance risk and cost. Results show that the RL-derived strategies consistently outperform baselines and operate near the efficient frontier, demonstrating a strong ability to optimise for risk and impact. These findings highlight the potential of reinforcement learning as a powerful tool in the trader's toolkit.