Group Theory

arXiv:math.GR

Finite groups, topological groups, representation theory, cohomology, classification and structure.

Looking for a broader view? This category is part of:

Trending in Group Theory

2512.15364

Uniform spectral gaps, non-abelian Littlewood-Offord and anti-concentration for random walks

We show that random walks on semisimple algebraic groups do not concentrate on proper algebraic subvarieties with uniform exponential rate of anti-concentration. This is achieved by proving a uniform spectral gap for quasi-regular representations of countable linear groups. The method makes key use of Diophantine heights and the Height Gap theorem. We also deduce a non-abelian version of the Littlewood--Offord inequalities and prove logarithmic bounds for escape from subvarieties. In a sequel to this paper, we will show how to transform this uniform gap into uniform expansion for Cayley graphs of finite simple groups of bounded rank $G(p)$ over almost all primes $p$.

2512.153641

Dec 2025Group Theory

2512.04531

A continuum of non-measure equivalent groups

We construct a continuum sized family $\{G_x\}_{x\in\{0,1\}^{\mathbb N}}$ of pairwise non-measure equivalent countable groups which have property (T) (hence are finitely generated), have zero $\ell^2$-Betti numbers of all orders, and are torsion-free.

2512.045311

Dec 2025Group Theory

Higher property T and below-rank phenomena of lattices

The purpose of this paper is twofold. We explore higher property T as an abstract group-theoretic property. In particular, we provide new operator-algebraic characterizations of higher property T. Then we turn to lattices in semisimple Lie groups. We relate higher property T to other cohomological, rigidity and geometric phenomena below the real rank. The second part outlines a conjectural framework that unifies these aspects and reviews recent advances.

2511.201923

Nov 2025Group Theory

2511.16400

An extreme boundary of acylindrically hyperbolic groups

We prove that every acylindrically hyperbolic group admits a minimal and extremely proximal action on a compact metrizable space. If there are no nontrivial finite normal subgroups, then the action is topologically free. This answers positively a question of Ozawa and the applications to $C^\ast$-algebras are discussed.

2511.164001

Nov 2025Group Theory

The commuting graph and a graph associated with centralizers

Let $G$ be a $p$-group. We begin to consider the relationship between the structure of the commuting graph and $|G:Z(G)|$. We also build a family of groups whose commuting graphs have more than one connected component whose diameter is at least $2$. For this, we introduce another graph related to the commuting graph that is associated with centralizers.

2511.119262

Nov 2025Group Theory

2511.10422

A family of accumulation points of non-free rational numbers

For any $q\in\mathbb{R}$, let $A:=\left(\begin{smallmatrix}1 & 1\\0 & 1\end{smallmatrix}\right), B_q:=\left(\begin{smallmatrix}1 & 0\\q & 1\end{smallmatrix}\right)$ and let $G_q:=\langle A,B_q\rangle\leqslant\operatorname{SL}(2,\mathbb{R})$. Kim and Koberda conjecture that for every $q\in\mathbb{Q}\cap(-4,4)$, the group $G_q$ is not freely generated by these two matrices. We generalize work of Smilga and construct families of $q$ satisfying the conjecture that accumulate at infinitely many different points in $(-4,4)$. We give different constructions of such families, the first coming from applying tools in Diophantine geometry to certain polynomials arising in Smilga's work, the second from sums of geometric series and the last from ratios of Pell and Half-Companion Pell Numbers accumulating at $1+\sqrt{2}$.

2511.104221

Nov 2025Group Theory

Modular elements in the lattice of monoid varieties

An element $x$ of a lattice $L$ is modular if $L$ has no five-element sublattice isomorphic to the pentagon in which $x$ would correspond to the lonely midpoint. In the present work, we classify all modular elements of the lattice of all monoid varieties.

2511.063581

Nov 2025Group Theory

2510.24092

Classifications of dimonoids with at most three elements

In this paper, we present complete classifications, up to isomorphism, of all two-element dimonoids, all commutative three-element dimonoids, and all abelian three-element dimonoids. We show that, up to isomorphism, there exist exactly 8 two-element dimonoids, of which 3 are commutative. Among these, 4 are abelian, and the remaining nonabelian dimonoids form 2 pairs of dual dimonoids. Furthermore, there are exactly 5 pairwise nonisomorphic trivial dimonoids of order 2. For dimonoids of order 3, we prove that there are precisely 14 pairwise nonisomorphic commutative dimonoids, including 12 trivial dimonoids and a single pair of nonabelian nontrivial dual dimonoids. We also establish that, up to isomorphism, there are 17 abelian dimonoids of order 3, consisting of 12 trivial commutative dimonoids and 5 noncommutative nontrivial ones. In addition, we demonstrate the existence of at least 26 pairwise nonisomorphic nonabelian noncommutative dimonoids of order 3. Among them, there are exactly 6 pairs of trivial dual dimonoids and at least 7 pairs of nontrivial dual dimonoids.

2510.240921

Oct 2025Group Theory

2510.23957

Simultaneous ping-pong for finite subgroups of reductive groups

Let $Γ$ be a Zariski-dense subgroup of a reductive group $\mathbf{G}$ defined over a field $F$. Given a finite collection of finite subgroups $H_i$ ($i \in I$) of $\mathbf{G}(F)$ avoiding the center, we establish a criterion to ensure that the set of elements of $Γ$ that form a free product with every $H_i$ (the so-called simultaneous ping-pong partners for $H_i$) is both Zariski- and profinitely dense in $Γ$. This criterion applies namely to direct products $\mathbf{G}$ of inner $\mathbb{R}$-forms of $\operatorname{(P)GL}_n$, and gives a positive answer to this particular case of a question asked by Bekka, Cowling and de la Harpe. For torsion elements, a complication arises due to the fact that a finite cyclic group can split into a direct product. When $\mathbf{G}$ is the multiplicative group of a semisimple algebra, we also give a more explicit method to obtain free products between two given finite subgroups, via first-order deformations. In the second half, we investigate the case where $\mathbf{G}$ is the multiplicative group of the group algebra $FG$ of a finite group $G$, and $Γ$ is the group of units of an order in $FG$. In this regard, we prove that the set of bicylic units that play ping-pong with a given shifted bicyclic unit, is Zariski- and profinitely dense, addressing a long-standing belief in the field of group rings. This result is deduced from the criterion above, combined with sharp existence results for well-behaved irreducible representations of $G$ that are center-preserving on a given subgroup.

2510.239571

Oct 2025Group Theory

2510.22134

Systems of imprimitivity for rank two quaternionic reflection groups

We revise the enumeration of the imprimitive rank two quaternionic reflection groups, adding missing groups and establishing isomorphisms between groups in the published tables. The isomorphisms are obtained as a consequence of the determination of the reflection groups with more than one system of imprimitivity. We find that there are primitive complex reflection groups which have infinitely many systems of imprimitivity when represented as quaternionic reflection groups.

2510.221341

Oct 2025Group Theory

Criteria for Classifying Prime Graphs of PSL(2, q)-Solvable Groups

For a finite group $G$, the prime graph $Γ(G)$ (also known as Gruenberg-Kegel graph) is defined to be the graph where the vertices are the primes that divide $|G|$ such that two vertices $p$ and $q$ share an edge if and only if there is an element of order $pq$ in $G$. The prime graphs of solvable groups have been classified. The prime graphs of groups whose noncyclic composition factors are isomorphic to a single nonabelian simple group $T$ where $|T|$ is divisible by three or four distinct primes have been classified except for the cases where $T = \operatorname{PSL}(2,q)$ for $q\neq 2^5$ and $|\operatorname{PSL}(2,q)|$ is divisible by exactly four primes. In this paper, we provide criteria for general classification results for certain classes of $T$, and then use them to classify the prime graphs of some $T$-solvable groups for $T$ a suitably small $\operatorname{PSL}(2, q)$-group. We also provide general results on the prime graphs of $T$-solvable groups where $T$ is a member of the possibly infinite family of groups $\operatorname{PSL}(2, 2^f)$ such that $f\geq 5, f$ is prime, and $|\operatorname{PSL}(2, 2^f)|$ is divisible by exactly four primes. This is the first paper to prove general results about the prime graphs of $T$-solvable groups where $T$ belongs to a large (probably infinite) family of groups.

2510.219791

Oct 2025Group Theory

2510.21387

Residual Finiteness Growth in Minimax Groups

If $g\in G$ is a non-trivial element in a residually finite group, then there exists by definition a finite group $Q$ and a homomorphism $\varphi: G \to Q$ such that $\varphi(g) \neq e$. The residual finiteness growth $\text{RF}_G$ of a finitely generated residually finite group $G$ estimates the size of $Q$ in terms of the word norm $\|g\|$ of the element $g\in G$. This function has been studied for several classes of groups, including free groups, lamplighter groups and nilpotent groups. For finitely generated linear groups $G\leq \text{GL}(m, \mathbb{C})$ this function is known to be bounded by $\text{RF}_G(r) \preceq r^{m^2+1}$, which is quadratic in $m$. This paper establishes an improved bound of the form $\text{RF}_G(r) \preceq r^{4k}$ with $k$ the Prüfer rank of $G$ for certain virtually solvable linear groups, namely minimax groups, a class which includes virtually polycyclic and Baumslag-Solitar groups. Moreover, the upper bound is invariant under taking finite extensions, and also establishes an improved polylogarithmic version for virtually nilpotent groups, generalizing the known exact bound for virtually abelian groups. If the group is not virtually nilpotent, we prove that $\text{RF}_G(r)$ is at least linear, improving a recent result.

2510.213871

Oct 2025Group Theory

2510.20959

$L^2$-torsion of automorphisms

We develop the theory of $L^2$-torsion of an automorphism of a group and compute it for every automorphism of a group which is hyperbolic and one-ended relative to a finite collection of virtually polycyclic groups. We also prove a combination formula for the $L^2$-torsion of a group in terms of the $L^2$-torsion of its stabilisers of a sufficiently nice action on a contractible space. We apply it to compute the $L^2$-torsion of a selection of CAT(0) lattices, of many relatively hyperbolic groups and their automorphisms, of higher dimensional graph manifolds, and of handlebody groups.

2510.209591

Oct 2025Group Theory

2510.14796

Novikov cohomology, finite domination, and cohomological dimension

We introduce the $Σ^*$-invariant of a group of finite type, which is defined to be the subset of non-zero characters $χ\in \mathrm H^1(G;\mathbb R)$ with vanishing associated top-dimensional Novikov cohomology. We prove an analogue of Sikorav's Theorem for this invariant, namely that $\mathrm{cd}(\ker χ) = \mathrm{cd}(G) - 1$ if and only if $\pm χ\in Σ^*(G)$ for integral characters $χ$. This implies that cohomological dimension drop is an open property among integral characters. We also study the cohomological dimension of arbitrary co-Abelian subgroups. The techniques yield a short new proof of Ranicki's criterion for finite domination of infinite cyclic covers, and in a different direction, we prove that the algebra of affiliated operators $\mathcal U(G)$ of a RFRS group $G$ has weak dimension at most one if and only if $G$ is an iterated (cyclic or finite) extension of a free group.

2510.147961

Oct 2025Group Theory

Fixed subgroups of generalised Baumslag-Solitar groups

We investigate fixed subgroups of automorphisms of generalised Baumslag-Solitar (GBS) groups. Our main results are for automorphisms leaving a Bass-Serre tree invariant, under the assumption that all edge stabilisers are strictly contained in the corresponding vertex stabilisers. We completely characterise which GBS groups admit such an automorphism with a fixed subgroup which is not finitely-generated. In doing so, we provide an infinite family of examples of non-finitely generated fixed subgroups in GBS groups. Dropping the above assumptions, we show that all finite order automorphisms of GBS groups have finitely generated fixed subgroups. Furthermore, we show that when the GBS graph is a tree, all automorphisms have finitely generated fixed subgroups.

2510.127161

Oct 2025Group Theory

2510.10754

Detecting the real line among one-parametric topological groups

We prove that a topological group is isomorphic to the real line if and only if it is a one-parameteric, metrizable, and not monothetic. This result is used in the authors' other paper to prove that one-parametric groups in strictly convex metric group all are topologically isomorphic to the real line. The example of the Bohr topology on the real line demonstrates that metrizability is an essential assumption in our first claim. This motivates further study to characterize the Bohr group topology as well as detect a monothetic one-parametric topological groups in a non-metrizable setting. Both issues are addressed and resolved in the present paper.

2510.107541

Oct 2025Group Theory

2510.10178

Embedding finitely generated free-by-cyclic groups in {finitely generated free}-by-cyclic groups

We refine Feighn--Handel's results on subgroups of mapping tori of free groups to the special case of free-by-cyclic groups. We use these refinements to show that any finitely generated free-by-cyclic group embeds in a {finitely generated free}-by-cyclic group. When the free-by-cyclic group is hyperbolic, it embeds in a hyperbolic {finitely generated free}-by-cyclic group as a quasi-convex subgroup. Combined with a result of Hagen--Wise, this implies that all hyperbolic free-by-cyclic groups are cocompactly cubulated.

2510.101781

Oct 2025Group Theory

Boundary actions of CAT(0) spaces: topological freeness and applications to $C^*$-algebras

In this paper, we study topological dynamics on the visual boundary and several combinatorial boundaries associated to $\operatorname{CAT}(0)$ spaces. Through verifying the freeness of Myrberg points on the boundaries, we prove that a large class of these boundary actions are topologically free strong boundary actions. These include certain visual boundary actions obtained from proper isometric actions of groups on proper $\operatorname{CAT}(0)$ spaces with rank-one elements, horofunction boundary actions from actions of irreducible finitely generated infinite non-affine Coxeter groups on the Caylay graphs, and Roller-type boundary actions from certain group actions on irreducible $\operatorname{CAT}(0)$ cube complexes. This in particular leads to a new proof of Kar-Sageev's topological freeness result for Roller boundary actions of $\operatorname{CAT}(0)$ cube complexes and generalizes Klisee's topological freeness result on horofunction boundaries from hyperbolic and right angled Coxeter groups to the general case. As applications to $C^*$-algebras, our work yields new examples of $C^*$-selfless groups and of exact, purely infinite, simple reduced crossed product $C^\ast$-algebras.

2510.056691

Oct 2025Group Theory

2510.05459

Metric criteria for fixed price of countable groups

We establish general criteria for a countable group $Γ$ to have fixed price 1 depending on a choice of left-invariant proper metric on $Γ$. We apply this criterion to show that if $Γ_1,Γ_2$ are two countable groups satisfying a certain growth condition then $Γ_1\times Γ_2$ has fixed price 1. For example, $Γ\times Γ$ has fixed price 1 for any countable group $Γ$.

2510.054592

Oct 2025Group Theory

2510.03492

Mixed identities in linear groups -- effective version

We show that MIF (mixed-identity-free) linear groups are sharply MIF and linearly MIF. Along the way we provide a self contained proof of the strong approximation theorem, and a new (probabilistic) variant of the super approximation theorem.

2510.034921

Oct 2025Group Theory

Related categories:

Commutative Algebra Algebraic Geometry Analysis of PDEs Algebraic Topology Classical Analysis and ODEs

405 papers

2601.03206

A short proof of a bound on the size of finite irreducible semigroups of rational matrices

I give a short proof of a recent result due to Kiefer and Ryzhikov showing that a finite irreducible semigroup of $n\times n$ matrices has cardinality at most $3^{n^2}$.

2601.03206Jan 2026

View

2601.02844

The Sequence Reconstruction of Permutations under Hamming Metric with Small Errors

The sequence reconstruction problem asks for the recovery of a sequence from multiple noisy copies, where each copy may contain up to $r$ errors. In the case of permutations on $n$ letters under the Hamming metric, this problem is closely related to the parameter $N(n,r)$, the maximum intersection size of two Hamming balls of radius $r$. While previous work has resolved $N(n,r)$ for small radii ($r \leq 4$) and established asymptotic bounds for larger $r$, we present new exact formulas for $r \in \{5,6,7\}$ using group action techniques. In addition, we develop a formula for $N(n,r)$ based on the irreducible characters of the symmetric group $S_n$, along with an algorithm that enables computation of $N(n,r)$ for larger parameters, including cases such as $N(43,8)$ and $N(24,14)$.

2601.02844Jan 2026

View

2601.01133

The diameter and dominating sets of the difference graph of a nilpotent group

Given a finite group $G$, the difference graph of $G$, denoted by $\mathcal{D}(G)$, is the difference of the enhanced power graph of $G$ and the power graph of $G$, with all isolated vertices removed. This paper mainly studies the dominating sets of the difference graph of a finite group. In particular, we prove that the diameter of the difference graph of a nilpotent group has an upper bound of $4$. Furthermore, we generalize and refine the result by Biswas et al. by classifying all nilpotent groups whose difference graph has diameter $k$, for each $k\le 4$.

2601.01133Jan 2026

View

2512.24357

On $R$-equivalence of Automorphism Groups of Associative Algebras

Let $A$ be a finite-dimensional associative $k$-algebra with identity. The primary aim of this paper is to study the rationality properties of the group of all $k$-algebra automorphisms of $A$, as an affine algebraic group over an arbitrary field $k$. We investigate mainly the $R$-equivalence property of the identity component of $\mathrm{Aut}_{k}(A)$ over a perfect field $k$.

2512.24357Dec 2025

View

2512.22410

Connectivity of $p$-subgroup posets with irreducible characters

Let $G$ be a finite group. For a prime $p$ and an integer $e \geq 0$, we denote by $Γ_{p,e}(G)$ the set of all pairs $(H, \varphi)$, where $H$ is a $p$-subgroup of $G$ of order greater than $p^e$ and $\varphi$ is a complex irreducible character of $H$. In this paper, we investigate the connected components of the poset $Γ_{p,e}(G)$. For the case $e = 0$, we prove that $Γ_{p,0}(G)$ is disconnected if and only if either $G$ has a strongly $p$-embedded subgroup, or every Sylow $p$-subgroup of $G$ contains a unique subgroup of order $p$. Furthermore, for $e = 1$ and $G$ a $p$-group, we show that the number of connected components of $Γ_{p,1}(G)$ equals the order of the intersection of all subgroups of $G$ of order $p^2$.

2512.22410Dec 2025

View

2512.21611

On automorphism groups of half-arc-transitive tetravalent graphs

We characterize connected tetravalent graphs $Γ$ which admit groups $M<H$ of automorphisms such that $Γ$ is $M$-half-arc-transitive and $H$-arc-transitive. Examples for each case are constructed, including a counter-example to a question asked by A. R. Rivera and P. Šparl in 2019 as well as the first example of tetravalent normal-edge-transitive non-normal Cayley graph on a nonabelian simple group.

2512.21611Dec 2025

View

2512.20524

On non-freeness of groups generated by two parabolic matrices with rational parameters: limit points and the orbit test

For $α\in \mathbb{R}$, let $$G_α:= \left< \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} , \begin{bmatrix} 1 & 0 \\ α& 1 \end{bmatrix} \right> < \mathrm{SL}_2 (\mathbb{R}).$$ K. Kim and the first author established the orbit test, which provides a sufficient condition for $G_α$ not to be a rank-$2$ free group. In this article, we present two main applications of the orbit test. First, using the corresponding modulo homomorphism, we show that the converse of the orbit test does not hold. In particular, we construct explicit counterexamples, all of which are rational. As another application, we construct sequences of non-free rational numbers converging to $3$. These sequences are given by $$ 3 + \frac{3}{2 (9 n - 1)} \quad \text{and} \quad 3 + \frac{9 n + 5}{3 (2 n + 1) (9 n + 4)},$$ and their construction relies on the orbit test together with a modified Pell's equation.

2512.20524Dec 2025

View

2512.19638

Rank-metric separation in irreducible representations of finite groups

We give a general lower bound on the rank of matrices of the form $ρ(h) - I$ with $ρ: G \rightarrow GL({\mathbb F}^n)$ an irreducible representation of a finite group $G$. The main tool in the proof is a (strengthening) of a reduction due to Efremenko from low rank matrices spanned by a few images of $ρ$ to Locally Decodable Codes (LDCs), which are a special kind of error correcting codes. We then apply the known results on 2-query LDCs to derive our rank bound.

2512.19638Dec 2025

View

On finite quotients of surface braid groups having order at most $127$

Let $Σ_b$ be a compact Riemann surface of genus $b \geq 2$ and let $\mathsf{P}_2(Σ_b)=π_1(Σ_b \times Σ_b - Δ)$ be the corresponding pure braid group on two strands. A finite quotient $\varphi \colon \mathsf{P}_2(Σ_b) \to G$ is called "admissible" if $\varphi$ does not factor through $π_1(Σ_b \times Σ_b)$. In this work we classify all admissible quotients of $\mathsf{P}_2(Σ_b)$ such that $|G| \leq 127$.

2512.18817Dec 2025

View

Nested Affine Buildings and Their Group Decompositions

In this paper, we construct a higher dimensional generalization of affine buildings and introduce a new structure, which we call Babel buildings. These buildings are non-connected, non-convex metric spaces of non-positive curvature. Despite their non-standard properties, Babel buildings provide an effective framework for studying the structure of groups acting on them. We analyze the metric and nesting structures of Babel buildings and derive key results regarding the group actions consistent with this new framework.

2512.18628Dec 2025

View

2512.18302

Sampling elements of a finite group: efficiency of the product replacement algorithm with an accumulator

Let $G$ be a finite group generated by $k$ elements. The well-known product replacement algorithm provides an effective method for sampling generating sets of $G$. We study a refinement of this algorithm that is designed to output individual elements of $G$. We show that after $O(k^2\log|G|)$ steps, the distribution of the output is close to uniform on $G$, which improves upon the best results known to date. The proof proceeds via spectral gap estimates and uses computer assisted calculations.

2512.18302Dec 2025

View

Block-transitive designs with a poset of imprimitive partitions

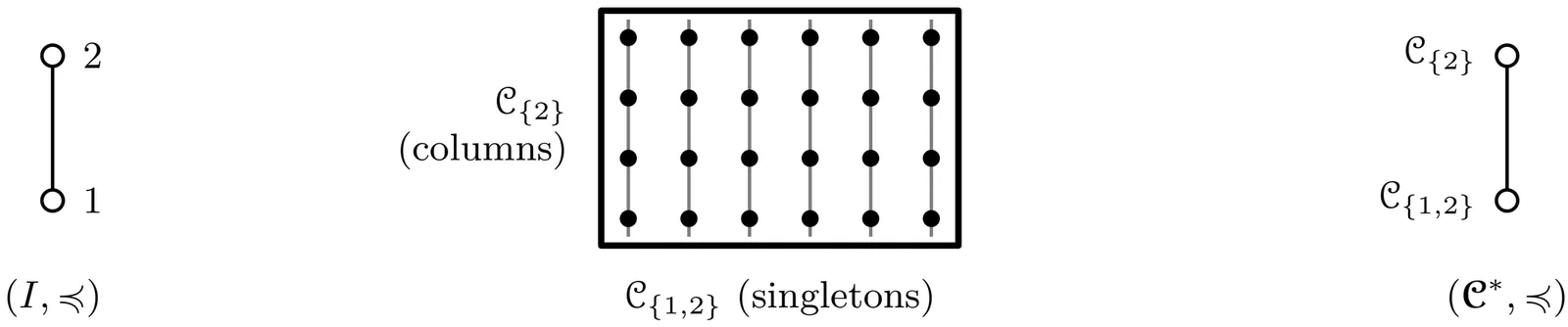
We study block designs which admit an automorphism group that is transitive on blocks and points, and leaves invariant every partition in a given finite poset of partitions of the point set. The full stabiliser $G$ of all the partitions in the poset is a generalised wreath product. We use the theory of generalised wreath products to give necessary and sufficient conditions, in terms of the `array' of a point-subset $B$, for the set of $G$-images of $B$ to form the block-set of a $G$-block-transitive $2$-design. This generalises previous results for the special cases where the poset is a chain or an anti-chain. We also give explicit infinite families of examples of $2$-designs for each poset involving three proper partitions, and for the famous $N$-poset with four partitions. (Posets with two proper partitions have been treated previously.) This suggests the problem of finding explicit examples for other posets.

2512.16246Dec 2025

View

2512.16079

Linear dimension of group actions

Two fundamental ways to represent a group are as permutations and as matrices. In this paper, we study linear representations of groups that intertwine with a permutation representation. Recently, D'Alconzo and Di Scala investigated how small the matrices in such a linear representation can be. The minimal dimension of such a representation is the \emph{linear dimension of the group action} and this has applications in cryptography and cryptosystems. We develop the idea of linear dimension from an algebraic point of view by using the theory of permutation modules. We give structural results about representations of minimal dimension and investigate the implications of faithfulness, transitivity and primitivity on the linear dimension. Furthermore, we compute the linear dimension of several classes of finite primitive permutation groups. We also study wreath products, allowing us to determine the linear dimension of imprimitive group actions. Finally, we give the linear dimension of almost simple finite $2$-transitive groups, some of which may be used for further applications in cryptography. Our results also open up many new questions about linear representations of group actions.

2512.16079Dec 2025

View

2512.15364

Uniform spectral gaps, non-abelian Littlewood-Offord and anti-concentration for random walks

2512.153641Dec 2025

View

2512.14324

Boundary actions of outer automorphism groups of Thompson-like groups

For every Cuntz--Krieger groupoid, we show that there is a topologically free boundary action of the outer automorphism group of its topological full group on the Hilbert cube. In particular, these outer automorphism groups, including the outer automorphism groups of all Higman--Thompson groups, are C*-simple.

2512.14324Dec 2025

View

2512.05569

PolExp growth for automorphisms of toral relatively hyperbolic groups

Let $G$ be a toral relatively hyperbolic group, and let $\varphi\in\mathrm{Aut}(G)$. We prove that, under iteration of $\varphi$, the conjugacy length $||\varphi^n(g)||$ of every element $g\in G$ grows like $n^dλ^n$ for some $d\in\mathbb{N}$ and some algebraic integer $λ\geq 1$. For a given $\varphi$, only finitely many values of $d$ and $λ$ occur as $g$ varies in $G$. The same statements hold for the growth of the word length $|\varphi^n(g)|$. For $G$ hyperbolic, we generalize polynomial subgroups: we show that, for a given growth type $n^dλ^n$ other than $1$, there is a malnormal family of quasiconvex subgroups $K_1,\dots,K_p$ such that a conjugacy class $[g]$ grows at most like $n^dλ^n$ if and only if $g$ is conjugate into one of the subgroups $K_i$.

2512.05569Dec 2025

View

Largest acylindrical actions of free-by-cyclic groups

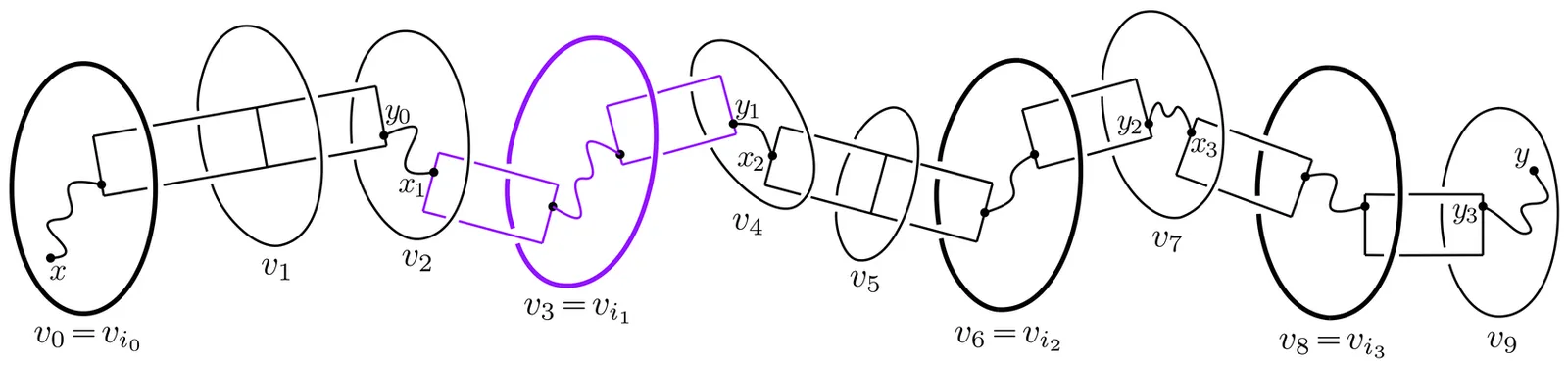
We show that every finitely generated free-by-cyclic group $G$ admits a largest acylindrical action on a hyperbolic space $X$ obtained by coning off maximal product subgroups of $G$. We characterise Morse geodesics of $G$ as those that project to quasigeodesics in $X$, thus showing that all finitely generated free-by-cyclic groups are Morse local-to-global. We also characterise the stable and strongly quasiconvex subgroups of $G$. Finally, we compute the Morse boundary for \{finitely generated free\}-by-cyclic groups with unipotent and polynomially growing monodromy.

2512.05293Dec 2025

View

2512.04531

A continuum of non-measure equivalent groups

2512.045311Dec 2025

View

2512.03885

The Protasov-Zelenyuk topology and ideal convergence

The so-called $T$-sequences $\mathbf u$ in a group $G$, and the related finest Hausdorff group topology $T_\mathbf u$ on $G$ that makes $\mathbf u$ a null sequence, were introduced by Protasov and Zelenyuk 35 years ago and since then they became a fundamental tool in the field of topological groups. More recently, in the abelian case, the subfamily of $T$-sequences called $TB$-sequences was introduced, as well as the finest precompact group topology $T_\mathbf{pu}$ that makes $\mathbf u$ a null sequence. Here we study the counterpart of all these notions with respect to ideal convergence in place of the classical notion of convergence of a sequence. Also, we study their relation to the already established field of $I$-characterized subgroups of compact abelian groups.

2512.03885Dec 2025

View

2512.02553

A New Approach from Lattice of Subgroup Sets to Generalized Solvable Extension Formations

In this paper, we establish the decomposition of morphisms from lattice of subgroup sets to generalized solvable extension formations. To achieve this, we develop a unified framework involving maximal subgroup functors, generating formation morphism and contraction-extension functors. In particular, solvability-induced sets of maximal subgroups are determined and generating formation morphism gives rise to generalized solvable extension formations.

2512.02553Dec 2025

View

Page 1 of 21