Rings and Algebras

arXiv:math.RA

Non-commutative rings and algebras, non-associative algebras, universal algebra and lattice theory, linear algebra, semigroups.

Looking for a broader view? This category is part of:

Algebra & Topology

Trending in Rings and Algebras

2512.12226

Asymmetry in Spectral Graph Theory: Harmonic Analysis on Directed Networks via Biorthogonal Bases (Adjacency-Operator Formulation)

Classical spectral graph theory and graph signal processing rely on a symmetry principle: undirected graphs induce symmetric (self-adjoint) adjacency/Laplacian operators, yielding orthogonal eigenbases and energy-preserving Fourier expansions. Real-world networks are typically directed and hence asymmetric, producing non-self-adjoint and frequently non-normal operators for which orthogonality fails and spectral coordinates can be ill-conditioned. In this paper we develop an original harmonic-analysis framework for directed networks centered on the \emph{adjacency} operator. We propose a \emph{Biorthogonal Graph Fourier Transform} (BGFT) built from left/right eigenvectors, formulate directed ``frequency'' and filtering in the non-Hermitian setting, and quantify how asymmetry and non-normality affect stability via condition numbers and a departure-from-normality functional. We prove exact synthesis/analysis identities under diagonalizability, establish sampling-and-reconstruction guarantees for BGFT-bandlimited signals, and derive perturbation/stability bounds that explain why naive orthogonal-GFT assumptions break down on non-normal directed graphs. A simulation protocol compares undirected versus directed cycles (asymmetry without non-normality) and a perturbed directed cycle (genuine non-normality), demonstrating that BGFT yields coherent reconstruction and filtering across asymmetric regimes.

2512.122262

Dec 2025Rings and Algebras

2512.11102

Higher Algebraic K-Theory of Non-Commutative Gamma Semirings: The Quillen and Waldhausen Spectra

In the companion paper~\cite{Gokavarapu_IJPA_2025}, we developed a classical algebraic K-theory for non-commutative $n$-ary $Γ$-semirings $(T,Γ)$ in terms of finitely generated projective $n$-ary $Γ$-modules and their automorphisms, and we identified the low K-groups $K_{0}(T,Γ)$ and $K_{1}(T,Γ)$ with appropriate Grothendieck and Whitehead groups. The present paper continues this programme by constructing and comparing several models for the higher algebraic K-theory of $(T,Γ)$. Starting from the Quillen-exact category $\mathcal{C} := T\text{-Mod}^{\mathrm{bi}}$ of bi-finite, slot-sensitive $n$-ary $Γ$-modules introduced earlier, we define the higher K-groups $K_{n}(T,Γ)$ via Quillen's Q-construction~\cite{Quillen73} on $\mathcal{C}$ and via Waldhausen's $S_{\bullet}$-construction~\cite{Waldhausen85} on the Waldhausen category of bounded chain complexes in $\mathcal{C}$. We prove a Gillet--Waldhausen type comparison theorem~\cite{GilletGrayson87} showing that the resulting Quillen and Waldhausen K-theory spectra are canonically weakly equivalent. Using dg-enhancements and the derived category of quasi-coherent sheaves on the non-commutative spectrum $\operatorname{Spec}_{T}^{\mathrm{nc}}(T)$~\cite{Gokavarapu_JRMS_2266}, we further identify these spectra with the K-theory of the small stable $\infty$-category of perfect complexes~\cite{Thomason90}. As consequences, we obtain functoriality, localization, and excision sequences~\cite{Weibel13}, and a derived Morita invariance statement for $K_{n}(T,Γ)$~\cite{Keller94}. These results show that algebraic K-theory of non-commutative $n$-ary $Γ$-semirings is a derived-geometric invariant of $\operatorname{Spec}_Γ^{\mathrm{nc}}(T)$ and reduce concrete computations to geometric dévissage and homological techniques developed in the earlier papers of the series.

2512.111022

Dec 2025Rings and Algebras

2512.11097

Projective Modules and Classical Algebraic K-Theory of Non-Commutative Gamma Semirings

In this paper, we initiate the study of algebraic K-theory for non-commutative $Γ$-semirings, extending the classical constructions of Grothendieck and Bass to this setting. We first establish the categorical foundations by constructing the category of finitely generated projective bi-$Γ$-modules over a non-commutative $Γ$-semiring $T$. We prove that this category admits an exact structure, allowing for the definition of the Grothendieck group $K_0^Γ(T)$. Furthermore, we develop the theory of the Whitehead group $K_1^Γ(T)$ using elementary matrices and the Steinberg relations in the non-commutative $Γ$-semiring context. We establish the fundamental exact sequences linking $K_0$ and $K_1$ and provide explicit calculations for specific classes of non-commutative $Γ$-semirings. This work lays the algebraic groundwork for future studies on higher K-theory spectra.

2512.110972

Dec 2025Rings and Algebras

2512.10263

Eigenvalues and equivalence classes of third-order symmetric tensors

This paper demonstrates that third-order real symmetric tensors cannot be classified up to equivalence by their eigenvalues only, thereby resolving a problem posed by Qi in 2006. By applying Harrison's center theory, we derive equivalence classes of $2 \times 2 \times 2$ symmetric tensors via the one-to-one correspondence with the canonical forms of their associated binary cubics. For such tensors, we compute the explicit characteristic polynomials and discover two previously unknown coefficients using the combination resultant. Pairs of third-order real symmetric tensors of all dimensions with identical eigenvalues but belonging to different equivalence classes are constructed to illustrate the inapplicability of eigenvalues for classification.

2512.102631

Dec 2025Rings and Algebras

The Equational Theories Project: Advancing Collaborative Mathematical Research at Scale

We report on the Equational Theories Project (ETP), an online collaborative pilot project to explore new ways to collaborate in mathematics with machine assistance. The project successfully determined all 22 028 942 edges of the implication graph between the 4694 simplest equational laws on magmas, by a combination of human-generated and automated proofs, all validated by the formal proof assistant language Lean. As a result of this project, several new constructions of magmas satisfying specific laws were discovered, and several auxiliary questions were also addressed, such as the effect of restricting attention to finite magmas.

2512.070871

Dec 2025Rings and Algebras

Classification of Homogeneous Odd Rota--Baxter Operators on a Modified Witt-Type Lie Superalgebra

We classify all homogeneous odd (i.e., parity-reversing) Rota--Baxter operators of weight zero on the modified Witt-type Lie superalgebra $W = \langle L_m, G_n \rangle_{m,n\in\Z}$. Our classification shows that nontrivial such operators are highly constrained: either $g \equiv 0$ and $f$ is arbitrary, or $g \not\equiv 0$ forces $f \equiv 0$, and $g$ must take one of several rigid forms dictated by the integer shift $k$ (necessarily odd when $g(0) \neq 0$). We prove that every Rota--Baxter operator on $W$ decomposes uniquely into even and odd homogeneous components; we restrict our attention to the odd case, which yields the full nontrivial structure. Furthermore, we show that all derivations of $W$ are inner, that no Rota--Baxter operator on $W$ is invertible, and we describe the induced super pre-Lie algebra structure together with its cohomological interpretation.

2512.042941

Dec 2025Rings and Algebras

2512.04190

Algebraic identities for linear operators on associative triple systems (long version)

We present the first classification of algebraic identities in 3 variables for linear operators on associative structures. We work in the context of associative triple systems, but since any associative algebra with product $xy$ becomes an associative triple system with product $xyz$, our results apply to associative algebras as well. This is the first time that Rota's classification problem for linear operators has been extended to algebras with an $n$-ary operation for $n \ge 3$. Our work is an application of computational linear algebra to the classification problem for linear operators. We begin with a generic operator identity with indeterminate coefficients. From this we use operadic partial compositions to derive a large sparse matrix whose nonzero entries are the indeterminates. We follow the rank principle which states that significant operator identities correspond to coefficients which produce submaximal rank of the matrix. For operator identities of multiplicity 1 (each term contains the operator once) we obtain 6 families with 1 parameter, and 1 isolated solution. For multiplicity 2, we obtain 6 families with 2 parameters, 27 families with 1 parameter, and 9 isolated solutions.

2512.041901

Dec 2025Rings and Algebras

2511.21797

Derived Functors, Resolutions, and Homological Dualities in n-ary Gamma-Semirings

This paper develops the homological backbone of the theory of non-commutative $n$-ary $Γ$-semirings. Starting from an $n$-ary $Γ$-semiring $(T,+,\tildeμ)$ and its $Γ$-ideals, we work in the slot-sensitive categories of left, right, and bi-$Γ$-modules, and endow the bi-module category with a Quillen exact structure compatible with the $n$-ary multiplication. Within this exact framework we construct bar-type projective resolutions and cofree-based injective resolutions under natural $Γ$-Noetherian and $Γ$-regular hypotheses on $T$, and we obtain finite projective resolutions for finitely presented bi-modules under $Γ$-Noetherian conditions. On this basis we define the derived functors $\ExtG$ and $\TorG$ for bi-$Γ$-modules, prove their balance with respect to projective and injective resolutions, establish long exact sequences and a Yoneda interpretation via iterated extensions, and construct Künneth-type spectral sequences and base-change isomorphisms. Interpreting bi-$Γ$-modules as quasi-coherent sheaves on the non-commutative $Γ$-spectrum $\SpecGnC{T}$, these homological invariants provide the appropriate derived language for a non-commutative $Γ$-geometry and prepare the ground for the spectral and geometric analysis carried out in the third part of this series.

2511.217971

Nov 2025Rings and Algebras

2511.20802

Exact Categories and Homological Foundations of Non-Commutative n-ary Gamma. Semirings

This paper establishes the homological and geometric foundations of non-commutative n-ary Gamma-semirings, unifying two previously distinct directions in Gamma-algebra: the derived Gamma-geometry developed for the commutative ternary case and the structural and spectral theory for general non-commutative n-ary systems. We introduce categories of left, right, and bi-Gamma-modules that respect positional asymmetry and prove that they form additive and exact categories in Quillen's sense. Within this setting, we construct projective and injective resolutions, define the derived functors Ext^Gamma and Tor_Gamma, and establish long exact sequences and spectral balance theorems in the n-ary regime. By extending sheaf-theoretic and homological tools to the non-commutative Gamma-spectrum Spec_Gamma^nc(T), we obtain a coherent framework of non-commutative derived Gamma-geometry that parallels the classical paradigms of Grothendieck and Kontsevich in homological algebra and non-commutative geometry. The framework developed here establishes the foundational exact-categorical and homological structures that enable Morita-type analyses and spectral interpretations in the subsequent parts of this series.

2511.208023

Nov 2025Rings and Algebras

2511.12555

Local superderivation and super-biderivation on generalized quaternion algebra

Let $\mathcal{H}^{a,b}$ be the generalized quaternion algebra over a unitary commutative ring. This paper aims to investigate super-biderivations and local superderivations on the generalized quaternion algebra, which is viewed as a class of Lie superalgebra. It turns out that on generalized quaternion algebras, any local superderivation is a superderivation.

2511.125551

Nov 2025Rings and Algebras

Explicit Baker--Campbell--Hausdorff Radii in Special Banach--Malcev Algebras of Shifts

We establish explicit convergence radii for the Baker--Campbell--Hausdorff (BCH) series in special Banach--Malcev algebras of shifts-those embeddable into a Banach alternative algebra. Under the continuity estimate $\|[x,y]\|\leq B\|x\|\|y\|$, the series converges absolutely whenever $B(\|x\|+\|y\|)<1/(4K)$, where $K\geq1$ bounds the absolute BCH coefficients. The constant $1/(4K)$ stems from a Catalan-number majorization and is sharp in the exponential-weight model. We compute $B$ explicitly for operator, exponential, polynomial, damped, and tree-like shift algebras, including the non-Lie split-octonionic (Zorn) algebra ($B=2$, $ρ=1/(8K)$). All results require the speciality assumption; the framework does not apply to general Malcev algebras. Geometrically, $ρ=1/(4KB)$ is the analyticity radius of the induced Moufang loop; numerically, it governs stability of BCH-type integrators.

2511.063571

Nov 2025Rings and Algebras

2511.03869

A topological approach to discrete restriction semigroups and their algebras

We introduce a general framework, based on étale topological categories, for studying discrete restriction semigroups and their algebras. Generalizing Paterson's universal groupoid of an inverse semigroup, we define the universal category ${\mathscr C}(S)$ of a restriction semigroup $S$ with local units as the category of germs of the spectral action of $S$ on the character space of its projection semilattice. This is an étale topological category, meaning that its domain map is a local homeomorphism, while its range map is only required to be continuous. We show that $S$ embeds into the universal Boolean restriction semigroup of compact slices of ${\mathscr C}(S)$ and apply this embedding to establish the following results: - a topological version of the ESN-type theorem for restriction semigroups by Gould and Hollings; - an extension to restriction semigroups of the Petrich-Reilly structure theorem for $E$-unitary inverse semigroups in terms of partial actions; - an isomorphism between the semigroup algebra of a restriction semigroup $S$ with local units and the convolution algebra of the universal category ${\mathscr C}(S)$, extending the seminal result by Steinberg. The paper is inspired by the work of Cockett and Garner and builds upon the earlier research of the author. It shows that the theory of restriction semigroups can be developed much further than was previously thought, as a natural extension of the inverse semigroup theory.

2511.038691

Nov 2025Rings and Algebras

2511.02544

Homological and Categorical Foundations of Ternary $Γ$-Modules and Their Spectra

Purpose: To develop a unified homological categorical foundation for commutative ternary Gamma semirings by formulating a general theory of ternary Gamma modules that integrates algebraic, geometric, and computational layers, extending the ideal theoretic and algorithmic bases of Papers A [Rao2025A] and B [Rao2025B1]. Methods: We axiomatize ternary Gamma modules and establish the fundamental isomorphism theorems, construct annihilator primitive correspondences, and prove Schur density embeddings. Categorical analysis shows that T Gamma Mod is additive, exact, and monoidal closed, enabling the definition of derived functors Ext and Tor via projective injective resolutions and yielding a tensor Hom adjunction. We develop geometric dualities between module objects and the spectrum Spec Gamma (T) and extend them to analytic, fuzzy, and computational settings. Results: The category T Gamma Mod admits kernels, cokernels, coequalizers, and balanced exactness; monoidal closure ensures internal Homs and coherent tensor Hom adjunctions. Derived functors Ext and Tor are well defined and functorial, with long exact sequences and base change compatibility. Schur density yields faithful embedding criteria, while annihilator primitive correspondences control primitivity and support theory. Geometric dualities provide contravariant equivalences linking submodule spectra with closed sets in Spec Gamma (T), persisting under analytic, fuzzy, and computational enrichments. Conclusion: These results complete the algebraic homological geometric synthesis for commutative ternary Gamma semirings, furnish robust tools for derived and spectral analysis, and prepare the framework for fuzzy and computational extensions developed in Paper D [Rao2025D], extending the algebraic framework first established in [Rao2025]

2511.025444

Nov 2025Rings and Algebras

2510.27450

On Modules Whose Pure Submodules Are Essential in Direct Summands

We introduce the notion of pure extending modules, a refinement of classical extending modules in which only pure submodules are required to be essential in direct summands. Fundamental properties and characterizations are established, showing that pure extending and extending modules coincide over von Neumann regular rings. As an application, we prove that pure extending modules admit decomposition patterns analogous to those in the classical theory, including a generalization of the Osofsky-Smith theorem: a cyclic module whose proper factor modules are pure extending decomposes into a finite direct sum of pure-uniform submodules. Additionally, we resolve an open problem of Dehghani and Sedaghatjoo by constructing a centrally quasi-morphic module that is not centrally morphic, arising from the link between pure-extending behavior and nonsingularity in finitely generated modules over Noetherian rings.

2510.274501

Oct 2025Rings and Algebras

2510.24513

Dagger categories of orthosets and the complex Hilbert spaces

An orthoset is a non-empty set $X$ together with a symmetric binary relation $\perp$ and a constant $0$ such that $x \not\perp x$ for any $x \neq 0$, and $0 \perp x$ for any $x$. Maps $f \colon X \to Y$ and $g \colon Y \to X$ between orthosets are said to form an adjoint pair if, for any $x \in X$ and $y \in Y$, $f(x) \perp g$ if and only if $x \perp g(x)$. Hilbert spaces, equipped with the usual orthogonality relation and the zero vector, provide the motivating examples of orthosets. The usual adjoints of bounded linear maps between Hilbert spaces are adjoints also in our sense. We investigate dagger categories of orthosets and maps between them, requiring that any morphism and its dagger form an adjoint pair. We indicate conditions under which such a category is unitarily dagger equivalent to the dagger category of complex Hilbert spaces and bounded linear maps.

2510.245131

Oct 2025Rings and Algebras

Prime and Semiprime Ideals in Commutative Ternary $Γ$-Semirings: Quotients, Radicals, Spectrum

The theory of ternary $Γ$-semirings extends classical ring and semiring frameworks by introducing a ternary product controlled by a parameter set $Γ$. Building on the foundational axioms recently established by Rao, Rani, and Kiran (2025), this paper develops the first systematic ideal-theoretic study within this setting. We define and characterize prime and semiprime ideals for commutative ternary $Γ$-semirings and prove a quotient characterization: an ideal $P$ is prime if and only if $T/P$ is free of nonzero zero-divisors under the induced ternary $Γ$-operation. Semiprime ideals are shown to be stable under arbitrary intersections and coincide with their radicals, providing a natural bridge to radical and Jacobson-type structures. A correspondence between prime ideals and prime congruences is established, leading to a Zariski-like spectral topology on $\mathrm{Spec}(T)$. Computational classification of all commutative ternary $Γ$-semirings of order $\leq 4$ confirms the theoretical predictions and reveals novel structural phenomena absent in binary semiring theory. The results lay a rigorous algebraic and computational foundation for subsequent categorical, geometric, and fuzzy extensions of ternary $Γ$-algebras.

2510.238854

Oct 2025Rings and Algebras

2510.20689

The trace Cayley-Hamilton theorem

In this expository paper, various properties of matrix traces, determinants and adjugate matrices are proved, including the *trace Cayley-Hamilton theorem*, which says that \[ kc_k + \sum_{i=1}^k \operatorname{Tr} (A^i) c_{k-i} = 0 \qquad \text{for every } k\in\mathbb{N} \] whenever $A$ is an $n\times n$-matrix with characteristic polynomial $\det (tI_n - A) = \sum_{i=0}^n c_{n-i} t^i$ over a commutative ring $\mathbb{K}$. While the results are not new, some of the proofs are. The proofs illustrate some general techniques in linear algebra over commutative rings.

2510.206892

Oct 2025Rings and Algebras

2510.14477

Modules With Descending Chain Conditions on Endoimages

We investigate endoartinian modules, which satisfy the descending chain condition on endoimages, and establish new characterizations that unify classical and generalized chain conditions. Over commutative rings, endoartinianity coincides with rings satisfying the strongly ACCR* with dim(R) = 0 and strongly DCCR* conditions. For principally injective rings, the endoartinian and endonoetherian rings are equivalent. Addressing a question of Facchini and Nazemian, we provide a condition under which isoartinian and Noetherian rings coincide, and we classify semiprime endoartinian rings as finite products of matrix rings over a division ring. We further show that endoartinianity is equivalent to the Kothe rings over principal ideal rings with central idempotents, and characterize such rings as finite products of artinian uniserial rings.

2510.144771

Oct 2025Rings and Algebras

2510.10972

Completely Positive Biquadratic Tensors

In this paper, we systemically introduce completely positive biquadratic (CPB) tensors and copositive biquadratic tensors. We show that all weakly CPB tensors are sum of squares tensors, the CPB tensor cone and the copositive biquadratic tensor cone are dual cone to each other. We also show that the outer product of two completely positive matrices is a CPB tensor, and the outer product of two copositive matrices is a copositive biquadratic tensor. We then study two easily checkable subclasses of CPB tensors, namely positive biquadratic Cauchy tensors and biquadratic Pascal tensors. We show that a biquadratic Pascal tensor is both strongly CPB and positive definite.

2510.109721

Oct 2025Rings and Algebras

2510.10124

Local Rigidity of Quasi--Lie Brackets on Quaternionic Banach Modules and Applications to Nonlinear PDEs

We establish a local rigidity theorem for quasi--Lie brackets on quaternionic Banach right modules. Under quantitative control of antisymmetry and Jacobi defects, we construct an explicit bilinear correction that preserves right $\mathbb{H}$--linearity and restores the exact Lie property. The approach combines a radial homotopy operator, a controlled Neumann-series inversion, and a finite-rank adjustment, all with explicit operator estimates. This constructive framework bridges quaternionic functional analysis with rigidity theory and yields concrete applications to nonlinear PDEs, including local well-posedness and Beale--Kato--Majda continuation criteria with explicit thresholds.

2510.101241

Oct 2025Rings and Algebras

Related categories:

Commutative Algebra Algebraic Geometry Analysis of PDEs Algebraic Topology Classical Analysis and ODEs

300 papers

2512.24881

Totally compatible structures on the radical of an incidence algebra

We describe totally compatible structures on the Jacobson radical of the incidence algebra of a finite poset over a field. We show that such structures are in general non-proper.

2512.24881Dec 2025

View

2512.21971

Post-Hopf algebroids, post-Lie-Rinehart algebras and geometric numerical integration

In this paper, we introduce the notion of post-Hopf algebroids, generalizing the pre-Hopf algebroids introduced in [Bronasco, Laurent, 2025] in the study of exotic aromatic S-series. We construct action post-Hopf algebroids through actions of post-Hopf algebras. We show that the universal enveloping algebra of a post-Lie-Rinehart algebra (post-Lie algebroid) is naturally a post-Hopf algebroid. As a byproduct, we construct the free post-Lie-Rinehart algebra using a magma algebra with a linear map to the derivation Lie algebra of a commutative associative algebra. Applications in geometric numerical integration on manifolds are given.

2512.21971Dec 2025

View

2512.16003

The Leavitt inverse semigroup of a separated graph

We introduce and study a new inverse semigroup associated to a separated graph $(E,C)$, which we call the \emph{Leavitt inverse semigroup}. This semigroup is obtained as a quotient of the separated graph inverse semigroup $\mathcal{S}(E,C)$, introduced in our previous paper [9], and it provides a canonical inverse semigroup model for the tame Leavitt path algebra $\mathcal{L}_K^\mathrm{ab}(E,C)$ over a commutative unital ring $K$. Our first main result describes the Leavitt inverse semigroup $\mathcal{LI}(E,C)$ as a restricted semidirect product of the free group on the edges of $E$ acting partially on a certain semilattice, which is isomorphic to the semilattice of idempotents of $\mathcal{LI}(E,C)$. This description, given in terms of Leavitt--Munn trees, yields a normal form for the elements of $\mathcal{LI}(E,C)$. We obtain a normal form for elements of $\mathcal{L}_K^\mathrm{ab}(E,C)$, leading to explicit linear bases for $\mathcal{L}_K^\mathrm{ab}(E,C)$. Building on this and on the structural properties of $\mathcal{LI} (E,C)$, we prove that the natural homomorphism from $\mathcal{LI}(E,C)$ to $\mathcal{L}_K^\mathrm{ab}(E,C)$ is injective, so that $\mathcal{LI}(E,C)$ embeds as the inverse semigroup generated by the canonical partial isometries in $\mathcal{L}_K^\mathrm{ab}(E,C)$. Further applications include the determination of natural bases of the kernel $\mathcal Q$ of the natural map from the tame Cohn algebra $\mathcal{C}_K^\mathrm{ab} (E,C)$ to the tame Leavitt path algebtra $\mathcal{L}_K^\mathrm{ab} (E,C)$, the computation of the socle, and a characterization of the isolated points of the spectrum. Several examples, such as the Cuntz separated graph and free separations, are discussed to illustrate the theory.

2512.16003Dec 2025

View

2512.13295

Reversible and Reversible-Complement Double Cyclic Codes over F4+vF4 and its Application to DNA Codes

In this article, we study the algebraic structure of double cyclic codes of length $(m, n)$ over $\mathbb{F}_4$ and we give a necessary and sufficient condition for a double cyclic code over $\mathbb{F}_4$ to be reversible. Also, we determine the algebraic structure of double cyclic codes of length $(m, n)$ over $\mathbb{F}_4+v\mathbb{F}_4$ with $v^2=v$, satisfying the reverse constraint and the reverse-complement constraint. Then we establish a one-to-one correspondence $ψ$ between the 16 DNA double pairs $S_{D_{16}} $ and the 16 elements of the finite ring $\mathbb{F}_4+v\mathbb{F}_4$. We also discuss the GC-content of DNA double cyclic codes.

2512.13295Dec 2025

View

2512.12460

A counterexample to DG version of Han's conjecture

In 2004, Han proposed the following conjecture: let $B$ be a finite-dimensional $k$-algebra. If $\mathrm{HH}_{n}(B)\neq 0$ for only finitely many $n\in \mathbb{Z}$, then $B$ is smooth. This conjecture can be generalized to the DG setting: let $B$ be a finite-dimensional DG $k$-algebra. If $\mathrm{HH}_{n}(B)\neq 0$ for only finitely many $n\in \mathbb{Z}$, then $B$ is smooth. In this note, we show that the DG generalization of Han's conjecture is false.

2512.12460Dec 2025

View

2512.12226

Asymmetry in Spectral Graph Theory: Harmonic Analysis on Directed Networks via Biorthogonal Bases (Adjacency-Operator Formulation)

2512.122262Dec 2025

View

2512.11703

The Veronese square of the dendriform operad

Veronese powers of operads were introduced in 2020 By Dotsenko, Markl, and Remm. The $m$-th Veronese power of a weight-graded operad $\mathcal{V}$ is the suboperad $\mathcal{V}^{[m]}$ generated by the operations of weight $m$. If $\mathcal{V}$ is generated by binary operations and governs the variety $\mathbf{V}$ of algebras, this gives a natural definition of the concept of $(m{+}1)$-ary $\mathbf{V}$-algebras. In particular, the Veronese square ($m=2$) corresponds to ternary algebras. We choose five generating operations for the Veronese square of the dendriform operad. We represent the dendriform operad as a suboperad of the Rota-Baxter operad, and express the quadratic relations satisfied by the generating operations as the kernel of a rewriting map. We use combinatorics of monomials and computational linear algebra to determine the kernel. We obtain 33 linearly independent quadratic relations defining the Veronese square.

2512.11703Dec 2025

View

2512.11688

Chein Automorphisms of Free Metabelian Anticommutative Algebras

We describe all automorphisms of a free metabelian anticommutative algebra of rank $n\geq 3$ over a field $K$ that move only one variable while fixing the others. Such automorphisms are called Chein automorphisms in the cases of free metabelian groups and free metabelian Lie algebras. We show that all automorphisms of a free metabelian anticommutative algebra of rank $n=2$ are linear, and that the simplest non elementary Chein automorphism of degree $3$ is absolutely wild for all $n\geq 3$.

2512.11688Dec 2025

View

2512.11540

Affinization of Zinbiel bialgebras and pre-Poisson bialgebras, infinite-dimensional Poisson bialgebras

The purpose of this paper is to construct infinite-dimensional Poisson bialgebras by the affinization of pre-Poisson algebras. There is a natural Poisson algebra structure on the tensor product of a pre-Poisson algebra and a perm algebra, and the Poisson algebra structure on the tensor product of a pre-Poisson algebra and a special perm algebra characterizes the pre-Poisson algebra. We extend such correspondences to the context of bialgebras, that is, there is a Poisson bialgebra structure on the tensor product of a pre-Poisson bialgebra and a quadratic $\bz$-graded perm algebra.In this process, we provide the affinization of Zinbiel bialgebras, and give a correspondence between symmetric solutions of the Yang-Baxter equation in pre-Poisson algebras and certain skew-symmetric solutions of the Yang-Baxter equation in the induced infinite-dimensional Poisson algebras. The similar correspondences for the related triangular bialgebra structures and $\mathcal{O}$-operators are given.

2512.11540Dec 2025

View

2512.11102

Higher Algebraic K-Theory of Non-Commutative Gamma Semirings: The Quillen and Waldhausen Spectra

2512.111022Dec 2025

View

2512.11097

Projective Modules and Classical Algebraic K-Theory of Non-Commutative Gamma Semirings

2512.110972Dec 2025

View

2512.10743

An embedding theorem for Nijenhuis Lie algebras

This paper introduces the Higman-Neumann-Neumann extension (HNN exten- sion; for short) for Nijenhuis Lie algebras and provides an embedding theorem. To this end, we employ the theory of Gröbner-Shirshov basis for Lie Ω-algebras in order to find a normal form for our construction. Then we show that every Nijenhuis Lie algebra embeds into its HNN-extension. Nijenhuis Lie algebras, Gröbner-Shirshov basis, HNN extension

2512.10743Dec 2025

View

2512.10567

Complete Structural Analysis of $q$-Heisenberg Algebras: Homology, Rigidity, Automorphisms, and Deformations

This paper establishes several fundamental structural properties of the $q$-Heisenberg algebra $\mathfrak{h}_n(q)$, a quantum deformation of the classical Heisenberg algebra. We first prove that when $q$ is not a root of unity, the global homological dimension of $\mathfrak{h}_n(q)$ is exactly $3n$, while it becomes infinite when $q$ is a root of unity. We then demonstrate the rigidity of its iterated Ore extension structure, showing that any such presentation is essentially unique up to permutation and scaling of variables. The graded automorphism group is completely determined to be isomorphic to $(\mathbb{C}^*)^{2n} \rtimes S_n$. Furthermore, $\mathfrak{h}_n(q)$ is shown to possess a universal deformation property as the canonical PBW-preserving deformation of the classical Heisenberg algebra $\mathfrak{h}_n(1)$. We compute its Hilbert series as $(1-t)^{-3n}$, confirming polynomial growth of degree $3n$, and establish that its Gelfand--Kirillov dimension coincides with its classical Krull dimension. These results are extended to a generalized multi-parameter version $\mathfrak{H}_n(\mathbf{Q})$, and illustrated through detailed examples and applications in representation theory and deformation quantization.

2512.10567Dec 2025

View

2512.10263

Eigenvalues and equivalence classes of third-order symmetric tensors

2512.102631Dec 2025

View

2512.09241

Embedding $K$-algebras into Leavitt algebra $L_K(1, 2)$

Since the commutative monoid $T = (\{0, 1\}, \vee)$ is a weak terminal object in the category of conical monoids with order units, there is a unital homomorphism from every Bergman $K$-algebra corresponding to a conical finitely generated commutative monoid into the Leavitt algebra $L_K(1,2)$, where $K$ is a field. This fact will be used to give a short proof that Leavitt path algebras associated with finite graphs with condition $(L)$ embed into $L_K(1,2)$, as well as provide criteria for an embedding of $M_s(L_{K}(1, m))$ in $M_s(L_{K}(1, n))$. As our second main result, we show that the Heisenberg equation $xy-yx=1$ cannot be realized in any Steinberg algebra, implying that the first Weyl algebra cannot be embedded into $L_K(1,2)$, giving an affirmative answer to a question of Brownlowe and Sorensen on the embeddability of $K$-algebras with a countable basis inside $L_K(1,2)$. Whereas, $L_K(E)$ cannot be graded-embedded into $L_K(1,2)$ in general, in the final section we show that $L_K(E)$ does admit a graded embedding into $L_K(1,2)\otimes_K L_K(1,2)$.

2512.09241Dec 2025

View

2512.07597

A Closed-form Solution to the Wahba Problem for Pairwise Similar Quaternions

We present a closed-form solution to Wahba's problem in the quaternion domain for the special case of two vector observations. Existing approaches, including Davenport's $q$-method, QUEST, Horn's method, and ESOQ algorithms, recover the optimal quaternion through the eigendecomposition of a $4\times4$ matrix or iterative numerical methods. Consequently, these methods do not reveal the analytic structure of the optimal quaternion. In this work, we derive an explicit analytical characterization of all quaternions that yield zero Wahba cost for the case $\ell=2$. Our approach builds on a connection between quaternion similarity, the singular Sylvester equation $aq=qb$, and quaternion square roots established in our previous work [1]. We provide (i) necessary and sufficient conditions under which the Wahba's cost function is zero and (ii) a closed-form parameterization of all such quaternions. This eliminates the need for eigenvalue computations and enables a direct algebraic understanding of the underlying geometry of Wahba's problem.

2512.07597Dec 2025

View

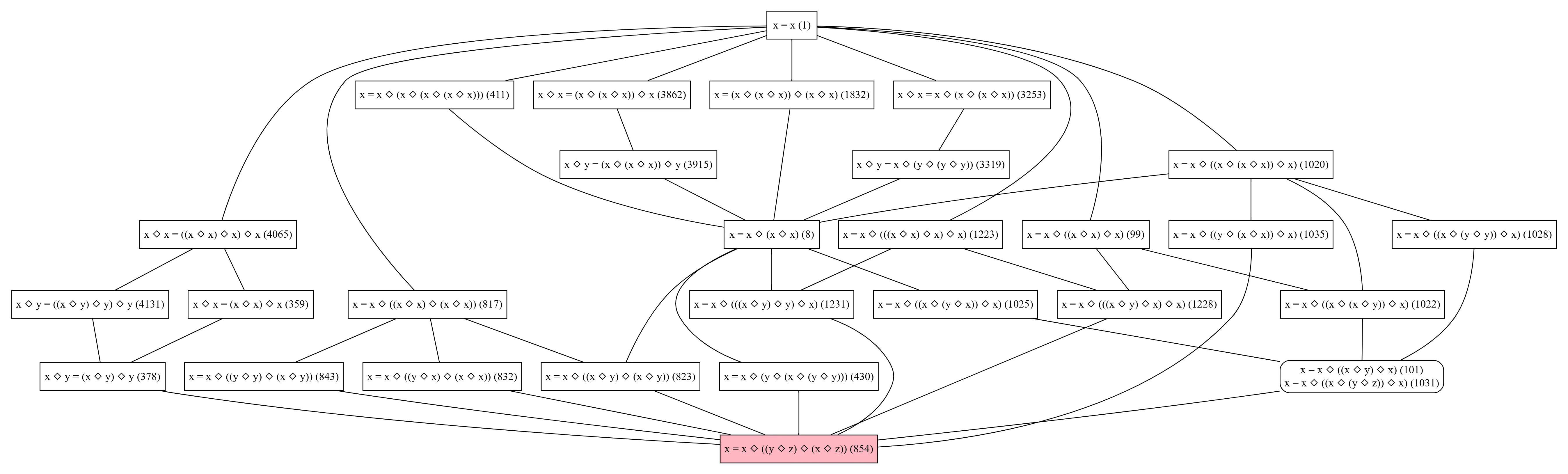
The Equational Theories Project: Advancing Collaborative Mathematical Research at Scale

2512.070871Dec 2025

View

2512.07903

Generalized Interlacing Families: New Error Bounds for CUR Matrix Decompositions

This paper introduces the concept of generalized interlacing families of polynomials, which extends the classical interlacing polynomial method to handle polynomials of varying degrees. We establish a fundamental property for these families, proving the existence of a polynomial with a desired degree whose smallest root is greater than or equal to the smallest root of the expected polynomial. Applying this framework to the generalized CUR matrix approximation problem, we derive a theoretical upper bound on the spectral norm of a residual matrix, expressed in terms of the largest root of the expected polynomial. We then explore two important special cases: the classical CUR matrix decompositions and the row subset selection problem. For classical CUR matrix decompositions, we derive an explicit upper bound for the largest root of the expected polynomial. This yields a tighter spectral norm error bound for the residual matrix compared to many existing results. Furthermore, we present a deterministic polynomial-time algorithm for solving the classical CUR problem under certain matrix conditions. For the row subset selection problem, we establish the first known spectral norm error bound. This paper extends the applicability of interlacing families and deepens the theoretical foundations of CUR matrix decompositions and related approximation problems.

2512.07903Dec 2025

View

2512.05755

The Commuting Graphs of Certain Solvable Lie Algebras

Let $Z(\cal L)$ be the center of a Lie algebra $\cal L$ with Lie bracket $[\cdot, \cdot]$. %We then define The commuting graph of $\cal L$ is then defined by the simple undirected graph $Γ({\cal L})=(V_{\cal L},E_{\cal L})$ in which the vertex set is $V_{\mathcal L}=\mathcal L \setminus Z(\mathcal L)$ and the set of edges $E_{\cal L}=\left\{ \{x,y\} \mid [x,y] =0 \right\}$. The main purpose of this paper is to accurately describe the connected components of the commuting graph of solvable Lie algebras of dimension at most 4.

2512.05755Dec 2025

View

2512.04769

Graded algebras with homogeneous involution and varieties of almost polynomial growth

An important aspect in the theory of algebras with polynomial identities is the study of the asymptotic behavior of the codimension sequence $c_n(A),\, n\geq 1,$ which measures the growth of polynomial identities of a given algebra $A$. In this context, graded identities naturally arise as prominent tools, since ordinary polynomial identities can be viewed as a particular case of graded identities. Moreover, as an involution does not necessarily preserve the homogeneous components of a grading, it is natural to consider the notion of a homogeneous involution. In this work, we investigate the behavior of the codimension sequence in the setting of $G$-graded algebras endowed with a homogeneous involution. More specifically, we characterize the varieties of polynomial growth in terms of the exclusion of a list of algebras from the variety. As a consequence, we provide the classification of the varieties with almost polynomial growth in this setting.

2512.04769Dec 2025

View

Page 1 of 15