Representation Theory

arXiv:math.RT

Linear representations of algebras and groups, Lie theory, associative algebras, multilinear algebra.

Looking for a broader view? This category is part of:

Trending in Representation Theory

2601.00674

Construction of simple quotients of Bernstein-Zelevinsky derivatives and highest derivative multisegments III: properties of minimal sequences

Let $F$ be a non-Archimedean local field. For an irreducible smooth representation $π$ of $\mathrm{GL}_n(F)$ and a multisegment $\mathfrak m$, one associates a simple quotient $D_{\mathfrak m}(π)$ of a Bernstein-Zelevinsky derivative of $π$. In the preceding article, we showed that \[ \mathcal S(π, τ) :=\left\{ \mathfrak m : D_{\mathfrak m}(π)\cong τ\right\} , \] has a unique minimal element under the Zelevinsky ordering, where $\mathfrak m$ runs for all multisegments. The main result of this article includes commutativity and subsequent property of the minimal sequence. At the end of this article, we conjecture some module structure arising from the minimality.

2601.006741

Jan 2026Representation Theory

2512.23285

Schur--Weyl duality for diagonalizing a Markov chain on the hypercube

We show how the tools of modern algebraic combinatorics -- representation theory, Murphy elements, and particularly Schur--Weyl duality -- can be used to give an explicit orthonormal basis of eigenfunctions for a "curiously slowly mixing Markov chain" on the space of binary $n$-tuples. The basis is used to give sharp rates of convergence to stationarity.

2512.232851

Dec 2025Representation Theory

2512.20472

Cuspidal character sheaves on graded Lie algebras II

In this paper we give a complete classification of cyclically graded semisimple Lie algebras that afford cuspidal character sheaves and determine the support of the cuspidal character sheaves. This constitutes a major step towards the explicit classification of cuspidal character sheaves for graded Lie algebras.

2512.204721

Dec 2025Representation Theory

2512.19045

Classical double Grothendieck transitions

Kirillov and Naruse have constructed double Grothendieck polynomials to represent the equivariant K-theory classes of Schubert varieties in the complete flag manifolds of types B, C, and D. We derive a recursive formula for these polynomials, extending certain K-theoretic transition equations known in type A to all classical types. As an application, we obtain an identity that expands the K-Stanley symmetric functions in types B, C, and D into positive linear combinations of K-theoretic Schur P- and Q-functions. We also resolve several positivity conjectures related to the skew generalizations of the latter functions.

2512.190451

Dec 2025Representation Theory

2512.14381

On the Positivity of Dihedral Branching Coefficients of the Symmetric and Alternating Groups

We determine precisely when the branching coefficients arising from the restriction of irreducible representations of the symmetric group $S_n$ to the dihedral subgroup $D_n$ are nonzero, and we establish uniform linear lower bounds outside a finite exceptional family. As a consequence, we recover and substantially generalize known positivity results for cyclic subgroups $C_n \leq S_n$. Analogous results are obtained for the alternating group $A_n$.

2512.143811

Dec 2025Representation Theory

Affine diagram categories, algebras and monoids

We introduce and study several affine (=annular in this paper) versions of the classical diagram algebras such as Temperley-Lieb, partition, Brauer, Motzkin, rook Brauer, rook, planar partition, and planar rook algebras. We give generators and relation presentation for them and their associated categories, study their representation theory, and the asymptotic behavior of tensor products of their representations in the monoid case.

2512.055101

Dec 2025Representation Theory

Pairs of eventually constant maps and nilpotent pairs

Tom Leinster gave a bijective correspondence between the set of operators on a finite-dimensional vector space $V$ and the set of pairs consisting of a nilpotent operator and a vector in $V$. Over a finite field this bijection implies that the probability that an operator be nilpotent is the reciprocal of the number of vectors in $V$. We generalize this correspondence to pairs of operators between pairs of vector spaces and determine the probability that a random pair of operators be nilpotent. We also determine the set-theoretical counterpart of this construction and compute the number of eventually constant pairs of maps between two finite sets, closely related to the number of spanning trees in a complete bipartite graph.

2512.033671

Dec 2025Representation Theory

Non-crossing partitions for exceptional hereditary curves

We introduce a new class of reflection groups associated with the canonical bilinear lattices of Lenzing, which we call reflection groups of canonical type. The main result of this work is a categorification of the corresponding poset of non-crossing partitions for any such group, realized via the poset of thick subcategories of the category of coherent sheaves on an exceptional hereditary curve generated by an exceptional sequence. A second principal result, essential for the categorification, is a proof of the transitivity of the Hurwitz action in these reflection groups.

2512.017291

Dec 2025Representation Theory

2511.22637

Lie groupoids, the Satake compactification and the tempered dual, I: The Satake groupoid

The (maximal) Satake compactification associated to a real reductive group $G$ is the closure of the symmetric space of all maximal compact subgroups of $G$ within the compact space of all closed subgroups of $G$. We shall present three different views of a groupoid that may be associated to the Satake compactification. To begin, we shall define our Satake groupoid, as we shall call it, as a topological groupoid, and as a special case of a general construction of Omar Mohsen. Then we shall give a Lie-theoretic account of the Satake groupoid, borrowing from work of Toshio Oshima. Finally we shall identify the Satake groupoid with the purely geometric $b$-groupoid of the Satake compactification, using the structure of the compactification as a smooth manifold with corners. In a subsequent paper we shall use the Satake groupoid to present a new proof of Harish-Chandra's principle, that all the tempered irreducible representations of $G$ may be constructed from discrete series representations using parabolic induction.

2511.226371

Nov 2025Representation Theory

2511.22635

Lie groupoids, the Satake compactification and the tempered dual, II: The Harish-Chandra principle

We give a geometric account of Harish-Chandra's principle that a tempered irreducible representation of a real reductive group is either square-integrable modulo center, or embeddable in a representation that is parabolically induced from such a representation. Our approach uses the Satake compactification, an associated groupoid that was constructed in the first paper of this series, and its $C^*$-algebra.

2511.226351

Nov 2025Representation Theory

2511.21671

Superalgebra deformations of web categories: Affine and cyclotomic webs

Let $\mathbb{k}$ be a characteristic zero domain. We define and study a diagrammatic monoidal $\mathbb{k}$-linear supercategory $\mathbf{Web}^{aff}_{A}$ associated to any locally unital Frobenius $\mathbb{k}$-superalgebra $A$. This category can be viewed variously as an affinization of the finite web category $\mathbf{Web}_{A}$ previously defined by the authors and Zhu, as a thickening of the degenerate affine wreath product algebras defined by Savage, or as a Frobenius deformation of affine web categories defined by Song and Wang. We show that there is an asymptotically faithful family of functors from $\mathbf{Web}^{aff}_{A}$ to the monoidal supercategory of endofunctors of $\mathfrak{gl}_n(A)$-modules for every $n \geq 1$, and use this to establish a basis of `decorated double coset diagrams' for morphism spaces in $\mathbf{Web}^{aff}_{A}$. We also define and establish basis results for the cyclotomic quotient category $\mathbf{Web}^Λ_{A}$ associated with a cyclotomic datum $Λ$.

2511.216711

Nov 2025Representation Theory

2511.18218

Classification of simple commutative algebras in the Delannoy category

The Delannoy category is an interesting pre-Tannakian category associated to the oligomorphic group $\mathbb{G}$ of automorphisms of the totally ordered set $(\mathbf{R}, <)$. By construction, it admits some obvious simple commutative algebras, corresponding to certain transitive $\mathbb{G}$-sets. We show that these account for all of the simple commutative algebras in the Delannoy category. Previous results of this kind have been limited to interpolation categories; since the Delannoy category cannot be obtained by interpolation, new methods are required.

2511.182181

Nov 2025Representation Theory

2511.15945

Representations of Cyclic Diagram Monoids

We introduce cyclic diagram monoids, a generalisation of classical diagram monoids that adds elements of arbitrary period by including internal components, with a view towards cryptography. We classify their simple representations and compute their dimensions in terms of the underlying diagram algebra. These go towards showing that cyclic diagram monoids possess representation gaps of exponential growth, which quantify their resistance as platforms against linear attacks on cryptographic protocols that exploit small dimensional representations.

2511.159452

Nov 2025Representation Theory

The limit cone and bounds on the growth indicator function

Given a real semisimple Lie group $G$ with finite center and a discrete subgroup $Γ\subset G$ whose limit cone is disjoint from two facets of the Weyl chamber we show that Quint's growth indicator function $ψ_Γ$ is bounded by the half sum of positive roots $ρ$, i.e. it has slow growth, implying that the representation $L^2(Γ\backslash G)$ is tempered. In particular, this holds for each $I$-Anosov subgroup provided that $I$ contains at least two distinct simple roots that are not interchanged by the opposition involution.

2511.069961

Nov 2025Representation Theory

Growth Problems of Quantum Groups

We study the asymptotic size of decompositions of tensor powers of tilting modules for quantum groups (mostly at a complex root of unity). In type A1 we obtain a sharp result for the number of indecomposable summands, explained by a one dimensional half-line random walk with a periodic congruence constraint. In general type we prove a universal law: the dominant part is governed only by the dimension of the module, while the correction depends only on the root system, so the asymptotic size is largely independent of the specific tilting module.

2511.067372

Nov 2025Representation Theory

2511.05768

A characterization of the Delannoy category by Adams operations

In recent joint work with Harman, we studied a pre-Tannakian category called the Delannoy category, and showed that it had numerous special properties. One of these is that the Adams operations on its Grothendieck group are trivial. In this paper, we prove three theorems inspired by this. Theorem A states that the Delannoy category is the unique semi-simple pre-Tannakian category having a generator that is fixed by the second Adams operation and whose exterior powers are simple. Theorem B states the Delannoy category is uniquely determined by its Grothendieck semi-ring (among semi-simple pre-Tannakian categories). This is reminiscent of Kazhdan--Wenzl's recognition theorem for quantum $\mathfrak{gl}_n$, and many subsequent results. Finally, Theorem C establishes some properties of pre-Tannakian categories where the second Adams operation fixes a generator.

2511.057681

Nov 2025Representation Theory

2511.03101

Coxeter groups and the proper joint spectrums of their faithful representations

In this paper, we analyze the faithful representations of the dihedral groups, and prove that the Coxeter groups can be determined by the proper joint spectrum of their faithful representations.

2511.031011

Nov 2025Representation Theory

2511.00939

The projective cover of the trivial module in characteristic $11$ for the sporadic simple Janko group $J_4$ revisited

This is a sequel to arXiv:2509.05805 [math.RT], where we have determined the $11$-modular projective indecomposable summands of the permutation character of $J_4$ on the cosets of an $11'$-subgroup of maximal order, amongst them the projective cover of the trivial module, up to a certain parameter. Here, we fix this parameter, by applying a new condensation method for induced modules which uses enumeration techniques for long orbits.

2511.009391

Nov 2025Representation Theory

2510.27311

Invariants in the cohomology of the complement of quaternionic reflection arrangements

Let $\mathcal A$ be a hyperplane arrangement in a vector space $V$ and $G \leq GL(V)$ a group fixing $\mathcal A$. In case when $G$ is a complex reflection group and $\mathcal A=\mathcal A(G)$ is its reflection arrangement in $V$, Douglass, Pfeiffer, and Röhrle studied the invariants of the $Q G$-module $H^*(M(\mathcal A);Q)$, the rational, singular cohomology of the complement space $M(\mathcal A)$ in $V$. In this paper we generalize the work in Douglass, Pfeiffer, and Röhrle to the case of quaternionic reflection groups. We obtain a straightforward generalization of the Hilbert--Poincaré series of the ring of invariants in the cohomology from the complex case when the quaternionic reflection group is complex-reducible according to Cohen's classification. Surprisingly, only one additional family of new types of Poincaré polynomials occurs in the quaternionic setting which is not realised in the complex case, namely those of a particular class of imprimitive irreducible quaternionic reflection groups. Finally, we discuss bases of the space of $G$-invariants in $H^*(M(\mathcal A);Q)$.

2510.273111

Oct 2025Representation Theory

2510.26252

Non-commutative crepant resolutions of toric singularities with divisor class group of rank one

We prove the existence and give a classification of toric non-commutative crepant resolutions (NCCRs) of Gorenstein toric singularities with divisor class group of rank one. We prove that they correspond bijectively to non-trivial upper sets in a certain quotient of the divisor class group equipped with a certain partial order. By this classification, we show that for such toric singularities, all toric NCCRs are connected by iterated Iyama-Wemyss mutations.

2510.262521

Oct 2025Representation Theory

Related categories:

Commutative Algebra Algebraic Geometry Analysis of PDEs Algebraic Topology Classical Analysis and ODEs

493 papers

Horn inequalities on a quiver with an involution

Derksen and Weyman described the cone of semi-invariants associated with a quiver. We give an inductive description of this cone, followed by an example of refinement of the inequalities characterising anti-invariant weights in the case of a quiver equipped with an involution.

2601.05089Jan 2026

View

The orientifold Temperley--Lieb algebra

We construct gradings on the simple modules of 2-boundary Temperley--Lieb algebras and symplectic blob algebras by realising the latter algebras as quotients of Varagnolo--Vasserot's orientifold quiver Hecke algebras. We prove that the symplectic blob algebras are graded cellular and provide a conjectural algorithm for calculating their graded decomposition matrices. In doing so, we give the first explicit family of finite-dimensional graded quotients of the orientifold quiver Hecke algebras, providing a new entry point for the structure of these algebras -- in the spirit of Libedinsky--Plaza's ``blob algebra approach'' to modular representation theory.

2601.04012Jan 2026

View

2601.04008

Affine Hecke and Schur algebras of type A without a square root of q

We provide an affine cellular structure on the extended affine Hecke algebra and affine $q$-Schur algebra of type $A_{n-1}$ that is defined over $\mathbb{Z}\left[q^{\pm1}\right]$, that is, without an adjoined $q^{\frac{1}{2}}$. This is with an eye to applications in the representation theory of $\mathrm{GL}_n(F)$ for a $p$-adic field $F$ over coefficient rings in which $p$ is invertible but does not have a square root, which have been a topic of recent interest. This is achieved via a renormalisation of the known affine cellular structure over $\mathbb{Z}\left[q^{\pm\frac{1}{2}}\right]$ at each left and right cell, which is chosen to ensure that the diagonal intersections remain subalgebras and that the left and right cells remain isomorphic. We furthermore show that the affine cellular structure on the Schur algebra has idempotence properties which imply finite global dimension, an important ingredient for the applications to representations of $p$-adic groups.

2601.04008Jan 2026

View

An Algebraic Representation Theorem for Linear GENEOs in Geometric Machine Learning

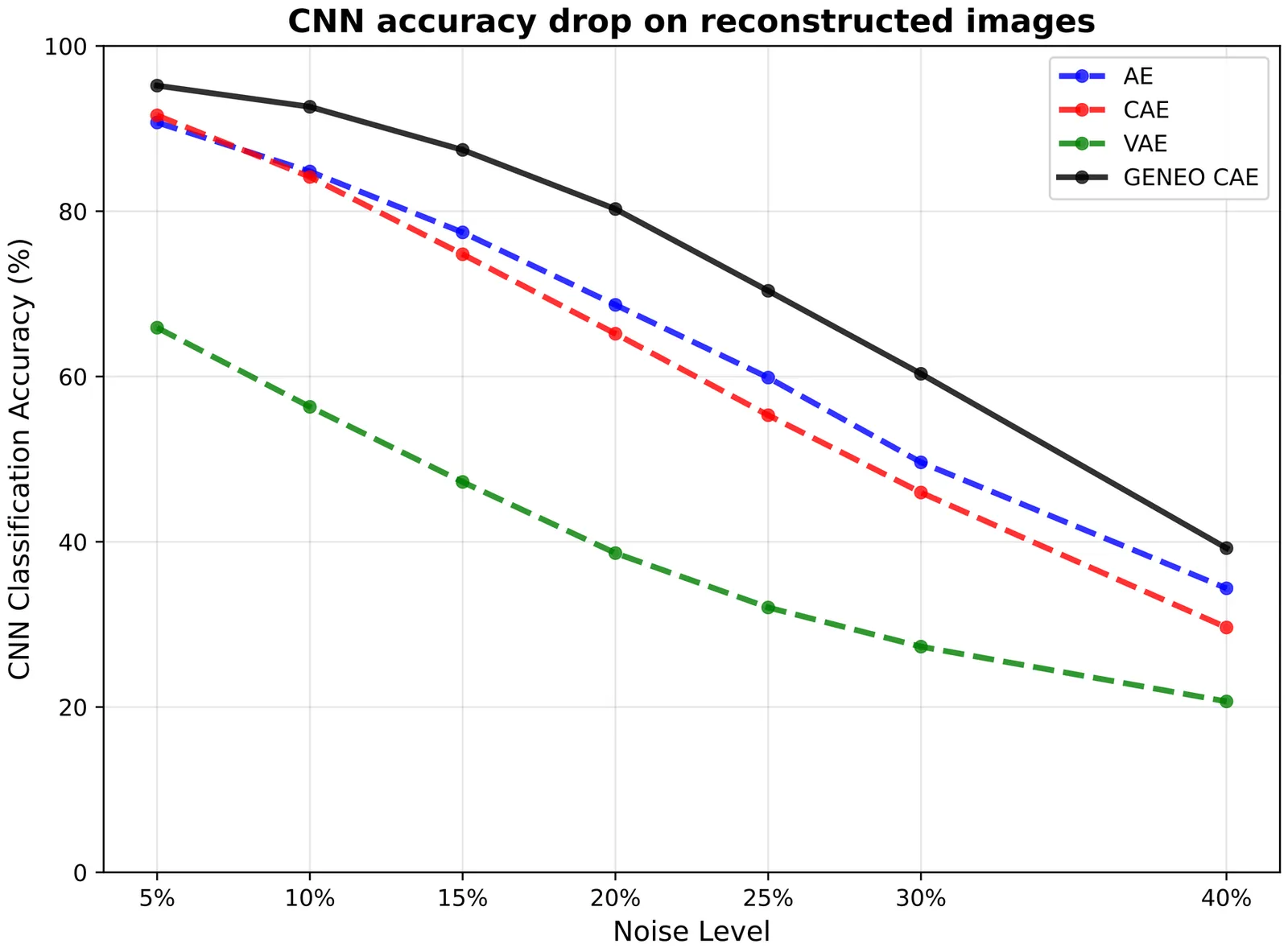
Geometric and Topological Deep Learning are rapidly growing research areas that enhance machine learning through the use of geometric and topological structures. Within this framework, Group Equivariant Non-Expansive Operators (GENEOs) have emerged as a powerful class of operators for encoding symmetries and designing efficient, interpretable neural architectures. Originally introduced in Topological Data Analysis, GENEOs have since found applications in Deep Learning as tools for constructing equivariant models with reduced parameter complexity. GENEOs provide a unifying framework bridging Geometric and Topological Deep Learning and include the operator computing persistence diagrams as a special case. Their theoretical foundations rely on group actions, equivariance, and compactness properties of operator spaces, grounding them in algebra and geometry while enabling both mathematical rigor and practical relevance. While a previous representation theorem characterized linear GENEOs acting on data of the same type, many real-world applications require operators between heterogeneous data spaces. In this work, we address this limitation by introducing a new representation theorem for linear GENEOs acting between different perception pairs, based on generalized T-permutant measures. Under mild assumptions on the data domains and group actions, our result provides a complete characterization of such operators. We also prove the compactness and convexity of the space of linear GENEOs. We further demonstrate the practical impact of this theory by applying the proposed framework to improve the performance of autoencoders, highlighting the relevance of GENEOs in modern machine learning applications.

2601.03910Jan 2026

View

2601.03128

On derived categories of module categories over multiring categories

Let $\mathcal{A}$ and $\mathcal{B}$ be subcategories of tensor categories $\mathcal{C}$ and $\mathcal{D}$, respectively, both of which are abelian categories with finitely many isomorphism classes of simple objects. We prove that if their derived categories $\mathbf{D}^b(\mathcal{A})$ and $\mathbf{D}^b(\mathcal{B})$ are left triangulated tensor ideals and are equivalent as triangulated $\mathbf{D}^b(\mathcal{C})$-module categories via an equivalence induced by a monoidal triangulated functor $F:\mathbf{D}^b(\mathcal{C})\rightarrow \mathbf{D}^b(\mathcal{D})$, then the original module categories $\mathcal{A}$ and $\mathcal{B}$ are themselves equivalent. We then apply this result to smash product algebras. Furthermore, the localization theory of module categories and triangulated module categories is investigated.

2601.03128Jan 2026

View

2601.03049

Classification of reductive homogeneous spaces satisfying strict inequality for Benoist-Kobayashi's $ρ$ functions

Let $G$ be a real reductive Lie group and $H$ a reductive subgroup of $G$. Benoist-Kobayashi studied when $L^2(G/H)$ is a tempered representation of $G$. They introduced the functions $ρ$ on Lie algebras and gave a necessary and sufficient condition for the temperedness of $L^2(G/H)$ in terms of an inequality on $ρ$. In a joint work with Y. Oshima, we considered when $L^2(G/H)$ is equivalent to a unitary subrepresentation of $L^2(G)$ and gave a sufficient condition for this in terms of a strict inequality of $ρ$. In this paper, we will classify the pairs $(\mathfrak{g}, \mathfrak{h})$ with $\mathfrak{g}$ complex reductive and $\mathfrak{h}$ complex semisimple which satisfy that strict inequality of $ρ$.

2601.03049Jan 2026

View

2601.02258

Categorification of local relative Langlands duality

We formulate the normalized period conjecture proposed by Ben-Zvi, Sakellaridis and Venkatesh in the framework of the categorical local Langlands correspondence and study its relation to distinction problems. Motivated by the work of Feng and Wang in the geometric setting, we verify the conjecture for the Iwasawa-Tate and Hecke periods, assuming the existence of the categorical local Langlands correspondence for $\mathrm{GL}_2$ with the Eisenstein compatibility.

2601.02258Jan 2026

View

2601.02188

Square integrability of regular representations on reductive homogeneous spaces

Let $G$ be a real reductive Lie group and $H$ a reductive subgroup of $G$. Benoist-Kobayashi studied when $L^2(G/H)$ is a tempered representation of $G$ and in particular they gave a necessary and sufficient condition for the temperedness in terms of certain functions on Lie algebras. In this paper, we consider when $L^2(G/H)$ is equivalent to a unitary subrepresentation of $L^2(G)$ and we will give a sufficient condition for this in terms of functions introduced by Benoist-Kobayashi. As a corollary, we prove the non-existence of discrete series for homogeneous spaces $G/H$ satisfying certain conditions.

2601.02188Jan 2026

View

2601.01738

The global Gan--Gross--Prasad conjecture for Fourier--Jacobi periods on unitary groups III: Proof of the main theorems

This is the third and the last of a series of three papers where we prove the Gan--Gross--Prasad conjecture for Fourier--Jacobi periods on unitary groups and an Ichino--Ikeda type refinement. Our strategy is based on the comparison of relative trace formulae formulated by Liu. In this paper, we compute the spectral expansions of these formulae and end the proof of the conjectures via a reduction to the corank zero case.

2601.01738Jan 2026

View

2601.01544

Hall $π$-subgroups and characters of $π'$-degree

We study the relationship between the existence of Hall $π$-subgroups and that of irreducible characters of $π'$-degree with prescribed fields of values in finite groups. This work extends a result of Navarro and Tiep from a single odd prime to multiple odd primes.

2601.01544Jan 2026

View

2601.01518

Shifted quantum groups via critical stable envelopes

Given a symmetric quiver with potential, we develop a geometric construction of shifted Yangians acting on the critical cohomologies of antidominantly framed quiver varieties with extended potentials, using the $R$-matrices constructed from critical stable envelopes. We relate such Reshetikhin type Yangians to Drinfeld type Yangians arising from critical cohomological Hall algebras. Several detailed examples, including the trivial, Jordan, and tripled Jordan quivers are explicitly computed. For symmetric quiver varieties with potentials, by using the smallness property of their affinization maps, we derive explicit formulas for quantum multiplication by divisors in terms of Casimir elements of the associated Lie (super)algebras, extending results from Nakajima quiver varieties to the critical setting. A similar formula in the antidominantly framed case is also obtained, which includes Hilbert schemes of points on $\mathbb C^3$ as examples.

2601.01518Jan 2026

View

2601.00674

Construction of simple quotients of Bernstein-Zelevinsky derivatives and highest derivative multisegments III: properties of minimal sequences

2601.006741Jan 2026

View

2601.00124

Hall induction for cotangent representations and wheel conditions

In this short note we study the Hall induction of cotangent representations of reductive groups. We prove its torsion freeness in Borel-Moore homology. In K-theory we find an analog of wheel conditions verified by the image of restriction map to the fixed point and consider examples.

2601.00124Dec 2025

View

2512.24870

Configuration Spaces of Finite Representation Type Algebras

To every finite-dimensional $\mathbb C$-algebra $Λ$ of finite representation type we associate an affine variety. These varieties are a large generalization of the varieties defined by "$u$ variables" satisfying "$u$-equations", first introduced in the context of open string theory and moduli space of ordered points on the real projective line by Koba and Nielsen, rediscovered by Brown as "dihedral co-ordinates", and recently generalized to any finite type hereditary algebras. We show that each such variety is irreducible and admits a rational parametrization. The assignment is functorial: algebra quotients correspond to monomial maps among the varieties. The non-negative real part of each variety has boundary strata that are controlled by Jasso reduction. These non-negative parts naturally define a generalization of open string integrals in physics, exhibiting factorization and splitting properties that do not come from a worldsheet picture. We further establish a family of Rogers dilogarithm identities extending results of Chapoton beyond the Dynkin case.

2512.24870Dec 2025

View

2601.00039

Quivers with Involutions and Shifted Twisted Yangians via Coulomb Branches II

To a quiver with involution, we show that there is an algebra homomorphism from the corresponding shifted twisted Yangian to the quantized Coulomb branch algebra of the 3d $\mathcal{N}=4$ involution-fixed part of the quiver gauge theory in the second symmetric power case.

2601.00039Dec 2025

View

2512.24158

Minimal Polynomials in Spin Representations of Symmetric and Alternating Groups

We determine the minimal polynomial of each element of the double cover $G$ of the symmetric or alternating group in every irreducible spin representation of $G$.

2512.24158Dec 2025

View

2512.23285

Schur--Weyl duality for diagonalizing a Markov chain on the hypercube

2512.232851Dec 2025

View

Computing quaternionic representations via twisted forms of Bruhat-Tits trees

This work is devoted to the study of representations of finite subgroups of the group of units of quaternion division algebras over a global or local field arising from the inclusion via extension of scalars splitting the algebra. Following a question by Serre, we study the set $\mathrm{IF}$ of conjugacy classes of integral representations that are conjugates of the given representation over the field. The set $\mathrm{IF}$ is often called the set of integral forms in the literature. In previous works we have seen that, for a given representation, the set $\mathrm{IF}$ can be indexed by the vertex set of a suitable subgraph of the Bruhat-Tits tree for the special linear group. In this work, we describe a construction that allows the simultaneous study of the set $\mathrm{IF}$ over different splitting fields. For this, we devise and use a theory of twisted Galois form of Bruhat-Tits trees. With this tool, we explicitly compute, in most cases, the cardinality of $\mathrm{IF}$ for the representation of the classical quaternion group of order $8$ studied by Serre, Feit and others, as much as for other similar groups.

2512.22713Dec 2025

View

Tableaux and orbit harmonics quotients for finite transformation monoids

We extend Grood's tableau construction of irreducible representations of the rook monoid and Steinberg's analogous result for the full transformation monoid. Our approach is characteristic-free and applies to any submonoid $\mathcal{M}(n)$ of the partial transformation monoid on an $n$-element set that contains the symmetric group. To achieve this, we introduce and study a functor from the category of rational representations of the monoid of $n \times n$ matrices to the category of finite dimensional representations of $\mathcal{M}(n)$. We establish two branching rules. Our main results describe graded module structures of orbit harmonics quotients for the rook, partial transformation, and full transformation monoids. This yields analogs of the Cauchy decomposition for polynomial rings in $n\times n$ variables.

2512.22353Dec 2025

View

2512.20525

Twisted character formula for toral supercuspidal representations

We establish an explicit formula for twisted Harish-Chandra characters of toral supercuspidal representations of p-adic reductive groups under several technical assumptions. Our setup especially includes the case of a quasi-split group equipped with a involution.

2512.20525Dec 2025

View

Page 1 of 25