Classical Physics
Newtonian and relativistic dynamics, classical field theory, classical electromagnetism, thermodynamics.
Newtonian and relativistic dynamics, classical field theory, classical electromagnetism, thermodynamics.
 2512.22898
2512.22898In this paper, we introduce "the Schrödinger plate." This is an infinite two-dimensional linear micro-polar elastic medium, with out-of-plane degrees of freedom, lying on a linear elastic foundation of a special kind. Any free motion of the plate can be corresponded to a solution of the two-dimensional Schrödinger equation for a single particle in the external potential field $V$. The specific dependence of the potential $V$ on the position is taken into account in the properties of the plate elastic foundation. The governing equations of the plate are derived as equations of the two-dimensional constraint Cosserat continuum using the direct approach. The plate dynamics can be described by the classical Germain-Lagrange equation for a plate, but the strain energy is different from the one used in the classical Kirchhoff-Love plate theory. Namely, the Schrödinger plate cannot be imagined as a thin elastic body composed of an isotropic linear material. The main property of the Schrödinger plate is as follows: the mechanical energy propagates in the plate exactly in the same way as the probability density propagates according to the corresponding Schrödinger equation.
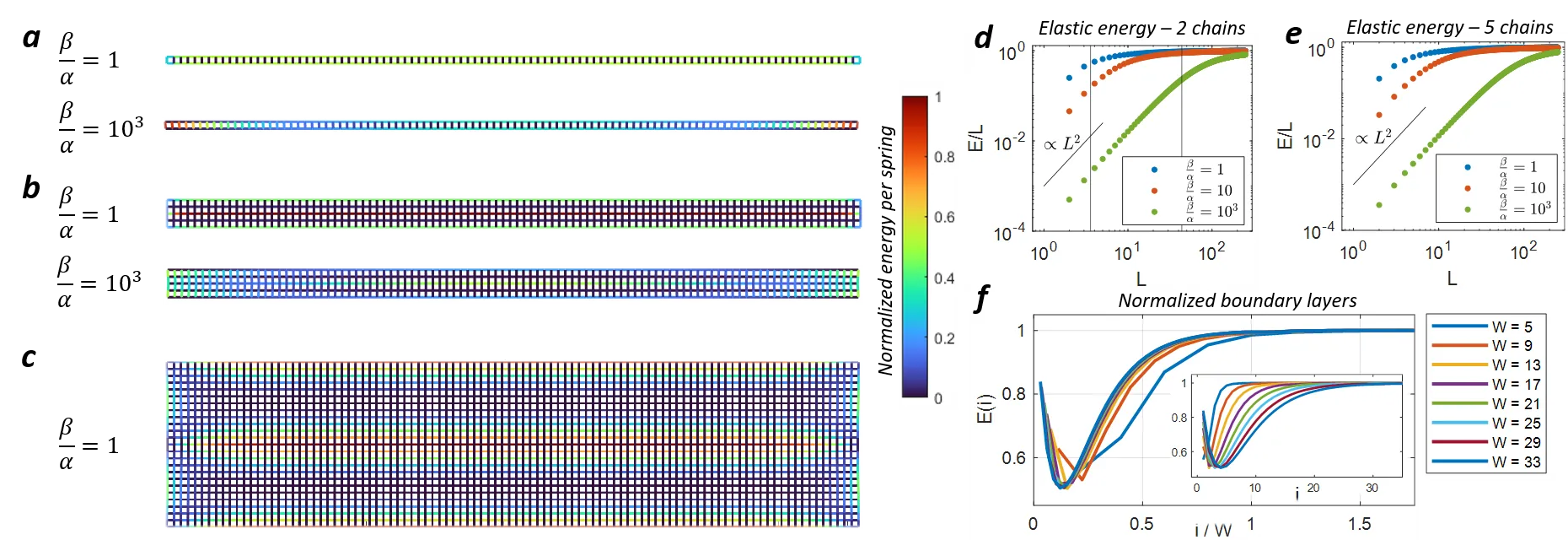
Cumulative geometric frustration can drive self-limited assembly and morphology selection through size-dependent energetic costs. However, the slenderness of quasi-one-dimensional systems generally suppresses the formation of long-range longitudinal gradients. We show that the suppression of longitudinal gradients can be overcome by tuning the ratio between the longitudinal and transverse (shear) moduli. We demonstrate the recovery of cumulative frustration across distinct quasi-one-dimensional systems, each frustrated through a different mechanism, by the introduction of a soft response mode.
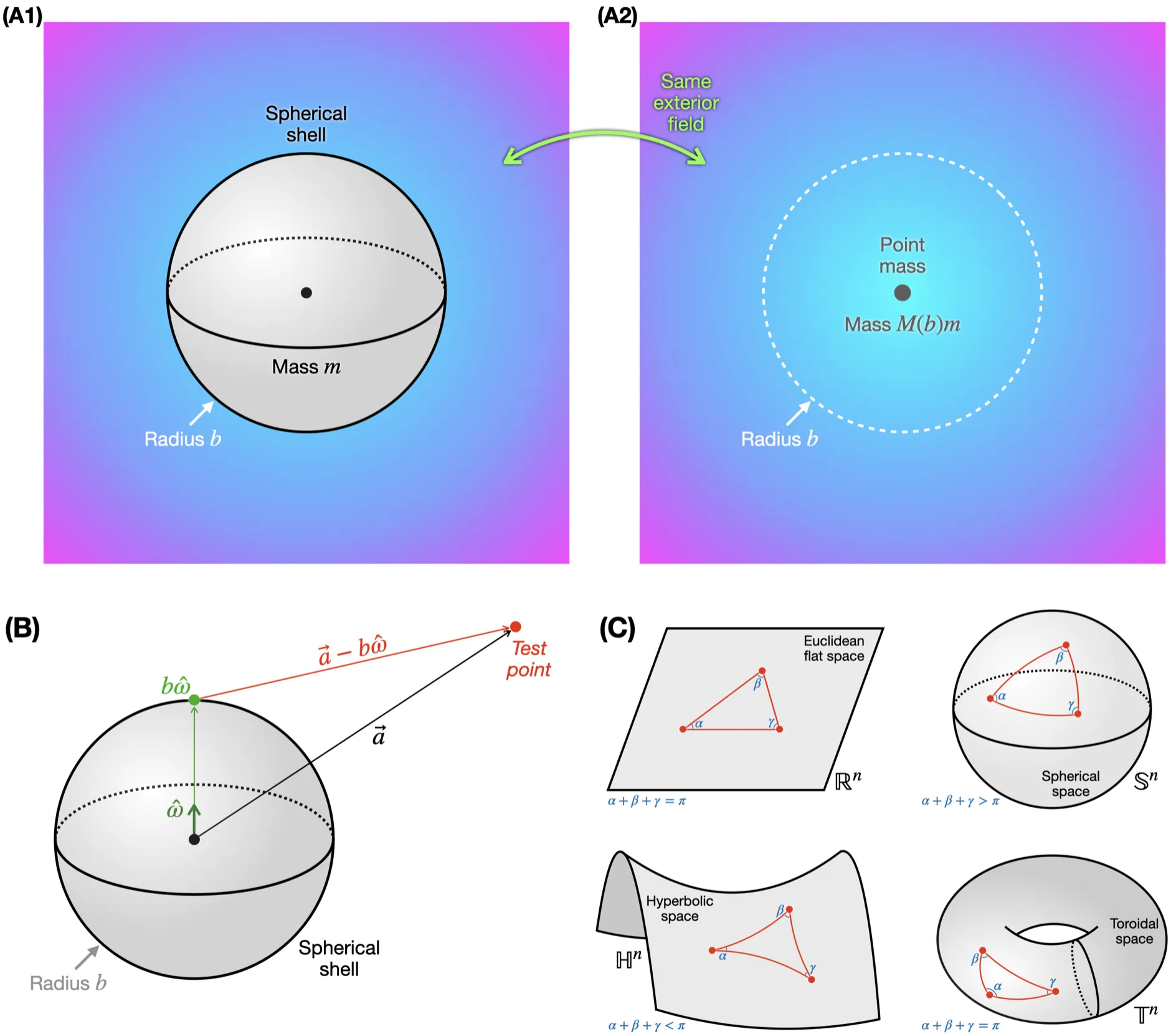
A gravitational potential has the spherical property when the field outside any uniform spherical shell is indistinguishable from that of a point mass at the center. We present the general potentials that possess this property on constant curvature spaces, using the Euler-Poisson-Darboux identity for spherical means. Our results are consistent with known findings in flat three-dimensional space and reduce to Gurzadyan's cosmological theorem when the rescaling factor is exactly $1$. Our approach naturally extends to nontrivial spatial topologies.
 2511.19571
2511.19571The notion of an infinite electromagnetic self energy of point charges (presumably electrons) is accepted by many electromagnetic textbooks. See, for instance,\cite{jdj,dg,rf}. However, each of these sources acknowledge that they don't understand that result. In this paper, we show that electrons must be point particles with no electromagnetic self energy.
The displacement current, introduced by Maxwell, has led to persistent confusion regarding its role in generating magnetic fields. To find a new way to understand classical magnetism, in this work, the displacement current is first decomposed into a localized internal part and an external field component by developing a discal regularization over the dipole distribution. Due to a surprising cancellation of the electric current by the internal displacement current, the magnetic field in the Coulomb gauge can be reformulated, in terms of the external component of the displacement current, as an instantaneous Biot-Savart law. The new expression allows for a reinterpretation of the generation of magnetic fields, viewing it as a magnetic effect related to the external displacement current, rather than directly to the electric current. The consistency of the Biot-Savart law with the Ampère-Maxwell law is thus confirmed, eliminating a dogged dispute in history. This result offers a potential recognition of the displacement current enigma. The regularization method is also applied to the polarization model to develop and refine the Clausius-Mossotti equation within the special Wigner-Seitz primitive-cell regularization.
 2511.13874
2511.13874In this paper we study universal deformations in anisotropic Cauchy elasticity. We show that the universality constraints of hyperelasticity and Cauchy elasticity for transversely isotropic, orthotropic, and monoclinic solids are equivalent. This implies that for each of these symmetry classes the universal deformations and the corresponding universal material preferred directions of hyperelastic and Cauchy elastic solids are identical. This is consistent with previous findings for isotropic solids. Universal deformations and material preferred directions are therefore independent of the existence or absence of a strain energy function.
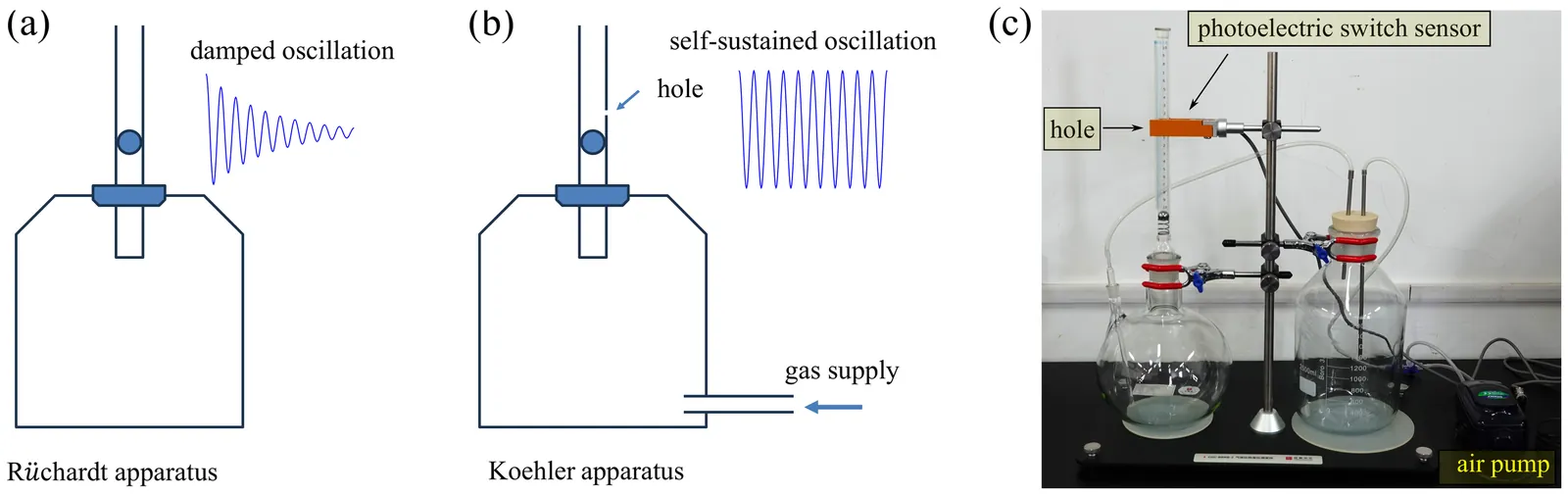
We revisit Koehler's experiment, a clever modification of Ruchardt's experiment designed to measure the ratio of specific heats of gas. The theory of self-sustained oscillations in Koehler's experiment was provided by Koehler (1950). However, its lengthy and dense analysis may pose challenges to readers due to the complexity of the calculations. Following Koehler's approximation for pressure changes, we explicitly present the model equations as piecewise linear differential systems and qualitatively analyze the periodic solutions from a geometric perspective. This concise and transparent approach addresses a fundamental question about Koehler's experiment: why is the oscillation frequency nearly equal to the Ruchardt frequency? Our analysis avoids intricate calculations and will be particularly helpful for teachers and students who encounter Koehler's experiment in general physics laboratory classes.

Shortly after the middle of the past century, a comprehensive presentation of Continuum Mechanics was written under supervision of Clifford Ambrose Truesdell III in two volumes of Siegfried Fluegge's Handbuch der Physik, a first in 1960 with Richard Toupin on The Classical Field Theories (the monster), including an Appendix on Tensor Analysis by Jerald LaVerne Ericksen, and a second volume in 1965 with Walter Noll on The Non-Linear Field Theories of Mechanics (the monsterino). Both nicknames are due to Truesdell. These contributions were gradually taken as turning points by the Mechanics Community worldwide, due to completeness of analysis and profoundness of documentation. Vastness of treatment acted however as a shield to careful reasoning on delicate but basilar notions which, in the wake of some scholars of the XIX century, were taken to be worthy of belief and incorporated in the presentation with a valuable historical background. Lack of engineering perspective didn't favour the necessary caution to be taken in facing a number of issues. Scholars in Continuum Mechanics, fascinated by the monumental work conceived and carried out by Truesdell and associates, did not dare any accurate revision. The analysis is here centred on unsatisfactory formulations presently disseminated in literature by followers of such authoritative treatment as Truesdell's opus magnum. The geometric approach in 4D Euclid spacetime adopted here is self-proposing even in classical context and provides clarity of notions, methods and results not achievable by the more familiar but less powerful and prone to confusing 3D treatment.
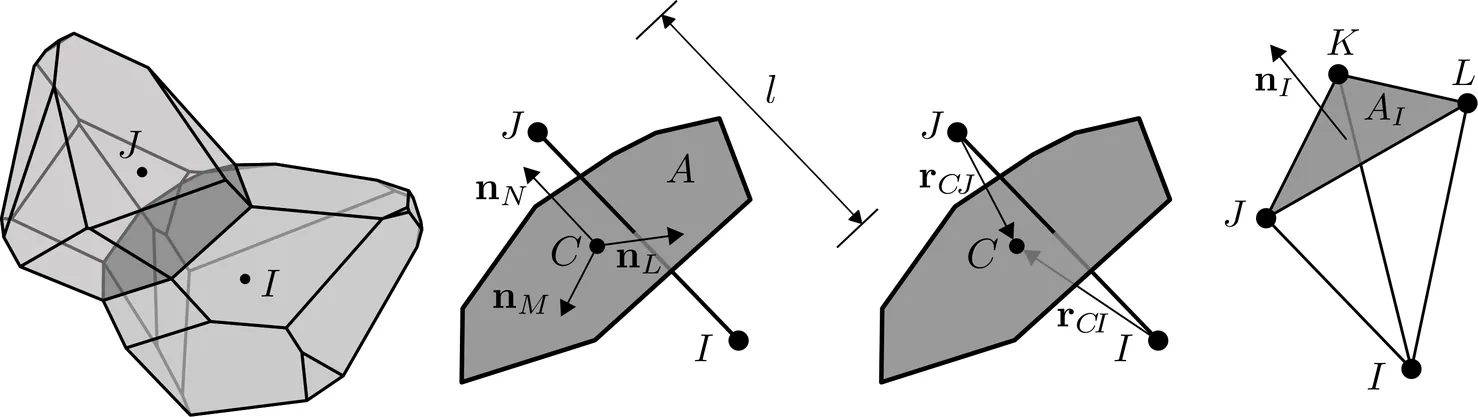
This article answers the question of whether homogenization of discrete fine-scale mechanical models, such as particle or lattice models, gives rise to an equivalent continuum that is of Cauchy-type or Cosserat-type. The study employs the machinery of asymptotic expansion homogenization to analyze discrete mechanical models with rotational degrees of freedom commonly used to simulate the mechanical behavior of heterogeneous solids. The proposed derivation has general validity in both stationary (steady-state) and transient conditions (assuming wavelength much larger that particle size) and for arbitrary nonlinear, inelastic fine-scale constitutive equations. The results show that the unit cell problem is always stationary, and the only inertia term appears in the linear momentum balance equation at the coarse scale. Depending on the magnitude of the local bending stiffness, mathematical homogenization rigorously identifies two limiting conditions that correspond to the Cauchy continuum and the Cosserat continuum. A heuristic combination of these two limiting conditions provides very accurate results also in the transition from one limiting case to the other. Finally, the study demonstrates that cases for which the Cosserat character of the homogenized response is significant are associated with non-physically high fine-scale bending stiffness and, as such, are of no interest in practice.
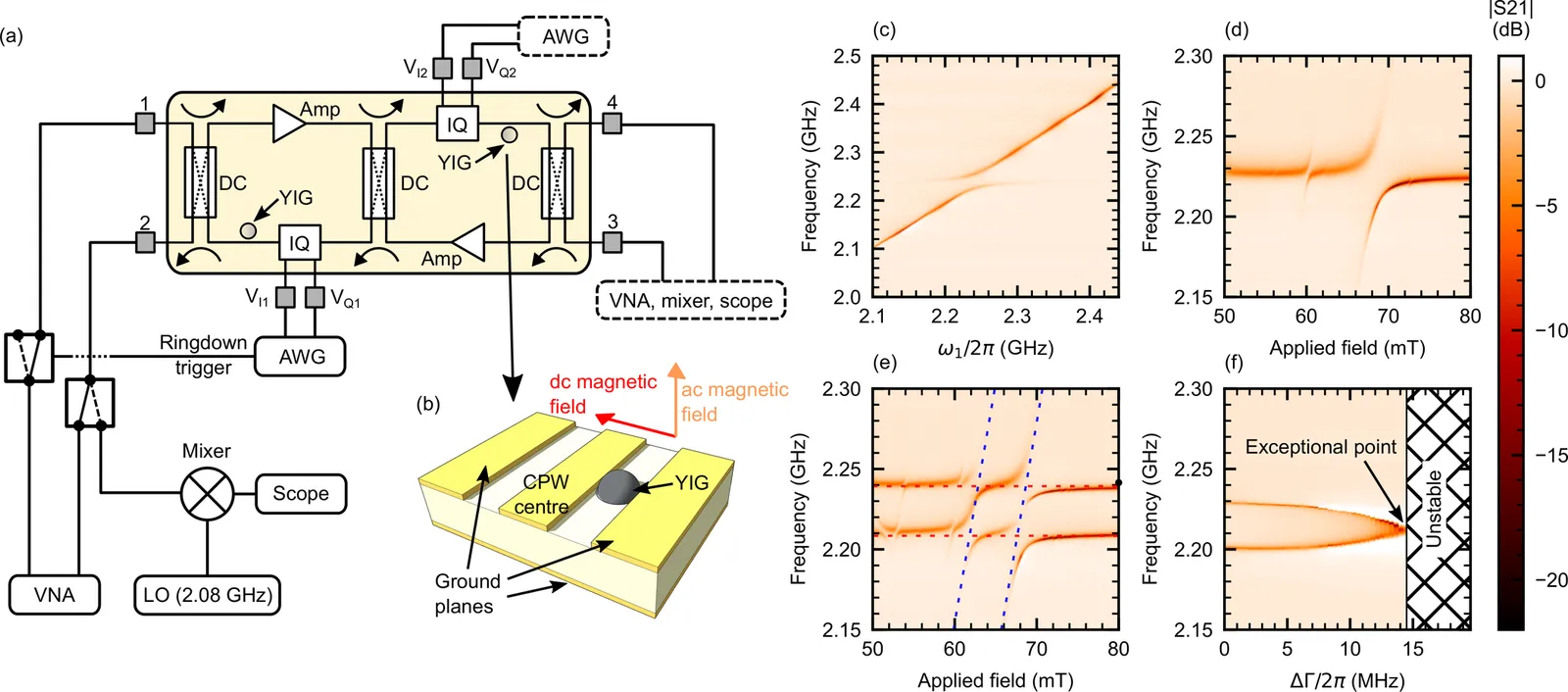
The amplitude of resonant oscillations in a non-Hermitian environment can either decay or grow in time, corresponding to a mode with either loss or gain. When two coupled modes have a specific difference between their loss or gain, a feature termed an exceptional point emerges in the excitations' energy manifold, at which both the eigenfrequencies and eigenmodes of the system coalesce. Exceptional points have intriguing effects on the dynamics of systems due to their topological properties. They have been explored in contexts including optical, microwave, optomechanical, electronic and magnonic systems, and have been used to control systems including optical microcavities, the lasing modes of a PT-symmetric waveguide, and terahertz pulse generation. A challenging problem that remains open in all of these scenarios is the fully deterministic and direct manipulation of the systems' loss and gain on timescales relevant to coherent control of excitations. Here we demonstrate the rapid manipulation of the gain and loss balance of excitations of a magnonic hybrid system on durations much shorter than their decay rate, allowing us to exploit non-Hermitian physics for coherent control. By encircling an exceptional point, we demonstrate population transfer between coupled magnon-polariton modes, and confirm the distinctive chiral nature of exceptional point encircling. We then study the effect of driving the system directly through an exceptional point, and demonstrate that this allows the coupled system to be prepared in an equal superposition of eigenmodes. We also show that the dynamics of the system at the exceptional point are dependent on its generalised eigenvectors. These results extend the established toolbox of adiabatic transfer techniques with a new approach for coherent state preparation, and provide a new avenue for exploring the dynamical properties of non-Hermitian systems.
 2511.02865
2511.02865Here we comment on the paper by Arthur D. Yaghjian, Phys. Rev. E 78, 046606 (2008) (arXiv:0805.0142). The author provides an equation of motion for a point charged particle in a certain regime of system parameters (on the other hand, claiming that in a different regime the classical equation of motion does not exist). The solutions of this equation (in the regime where it exists) presented in the paper show instantaneous jumps in the particle's velocity. We show that such jumps, in the case of a point particle, would generate infinite energy in the radiated electromagnetic field. Therefore, we claim that the point-particle limit used by the author is incorrect.
 2511.00571
2511.00571We present a minimal Path-Dependent Energy Lagrangian (PDEL) that generates, from a single action, the balance equations of mechanics and the entropy/heat equation for irreversible thermomechanical systems. The reversible part is the Helmholtz free energy, while irreversible effects enter through a history integral of channel powers. A single upper-limit/tangential variation rule makes the same instantaneous power appear as a dissipative force in the mechanical/internal-variable equations and as a positive source in the entropy/heat equation, closing the first law without double counting and guaranteeing nonnegative entropy production under mild monotonicity assumptions. PDEL preserves the classical Lagrangian mechanics while subsuming standard dissipative models (Kelvin--Voigt viscosity, diffusion) and their viscous heating, and clarifies the reversible character of thermo-mechanical cross terms. The formulation offers a compact alternative to Rayleigh/Onsager appendices and GENERIC/metriplectic brackets, with limited algebraic complexity and straightforward extension to multiphysics.
We study the influence of perturbations in the three dimensional isotropic harmonic oscillator problem considering different perturbing force laws and apply our results in the context of celestial mechanics, particularly in the movement of stars in stellar clusters. We use a method based on the Runge-Lenz tensor, so that our results are valid for any eccentricity of the unperturbed orbits of the oscillator. To establish basic concepts, we start by considering two cases, namely: a Larmor and a keplerian perturbation; and show that, in both cases, the perturbed orbits will precess. After that, we consider the more general problem of a central perturbation with any power-law dependence, that also only causes precession. Then, we consider precessionless perturbations caused by an Euler force and by the non-central dragging forces of the form $\boldsymbol{δF}=-γ_nv^{n-1}\boldsymbol{v}$, where $\boldsymbol{v}$ is the velocity of the particle and $γ_n\geq0$. We demonstrate that, in the case of a linear drag $(n=1)$, the orbits eccentricities remains constant. In contrast to what occurs in the well-known Kepler problem, for $n>1$ the orbit becomes increasingly eccentric. In the case $n=-3$, where the force is interpreted as a Chandrasekhar friction, we show that the eccentricity diminishes over time. We finish this work by making a few comments about the relevance of the main results.
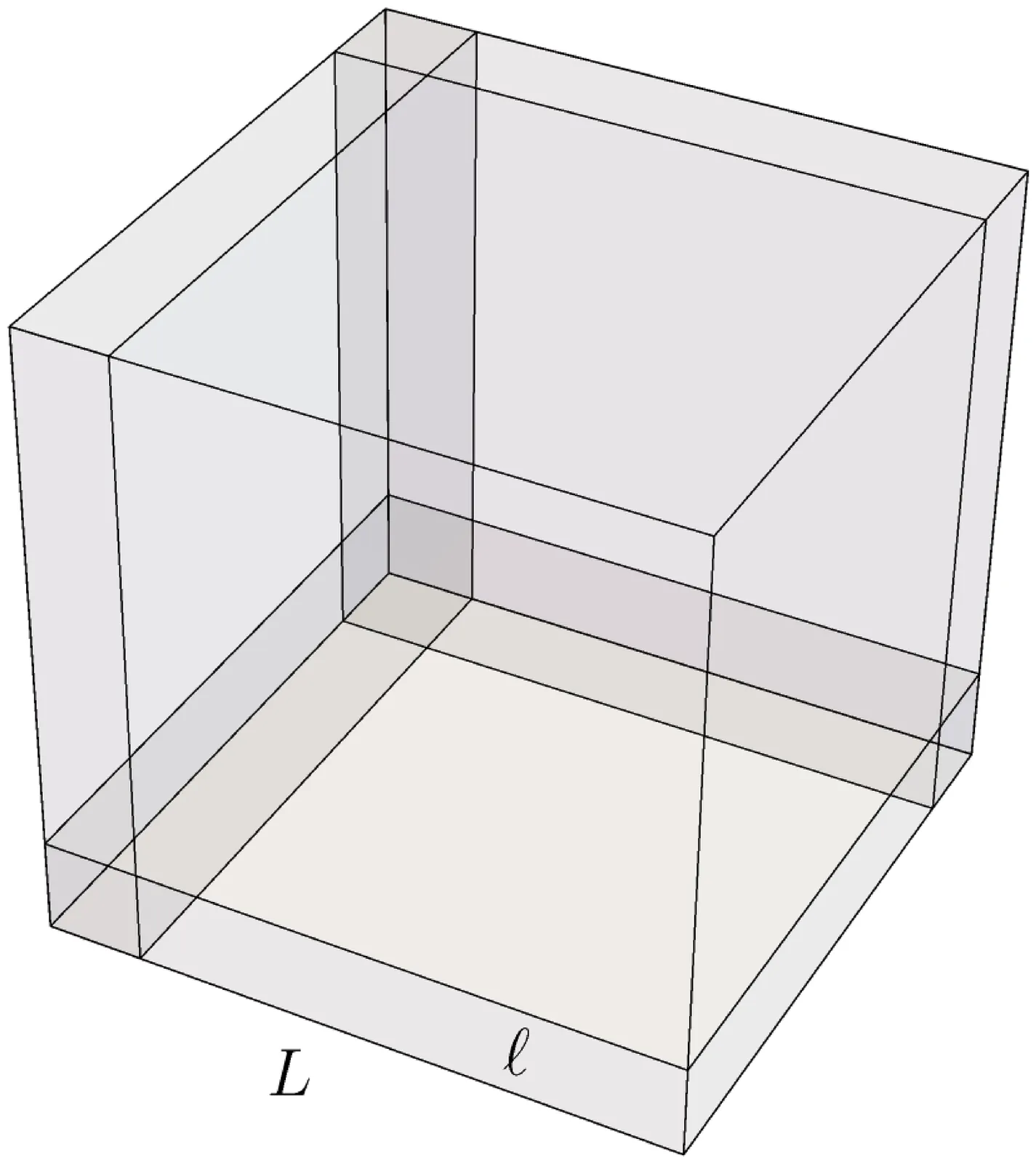
For a gas confined in a container, particle-wall interactions produce modifications to the partition function involving the average surface density of gas particles. While such correlations have a vanishing effect in the thermodynamic limit, examining them is beneficial for a sharper understanding of how the limit is attained. We contrast a classical and a quantum model of particle-wall correlations within the canonical ensemble.
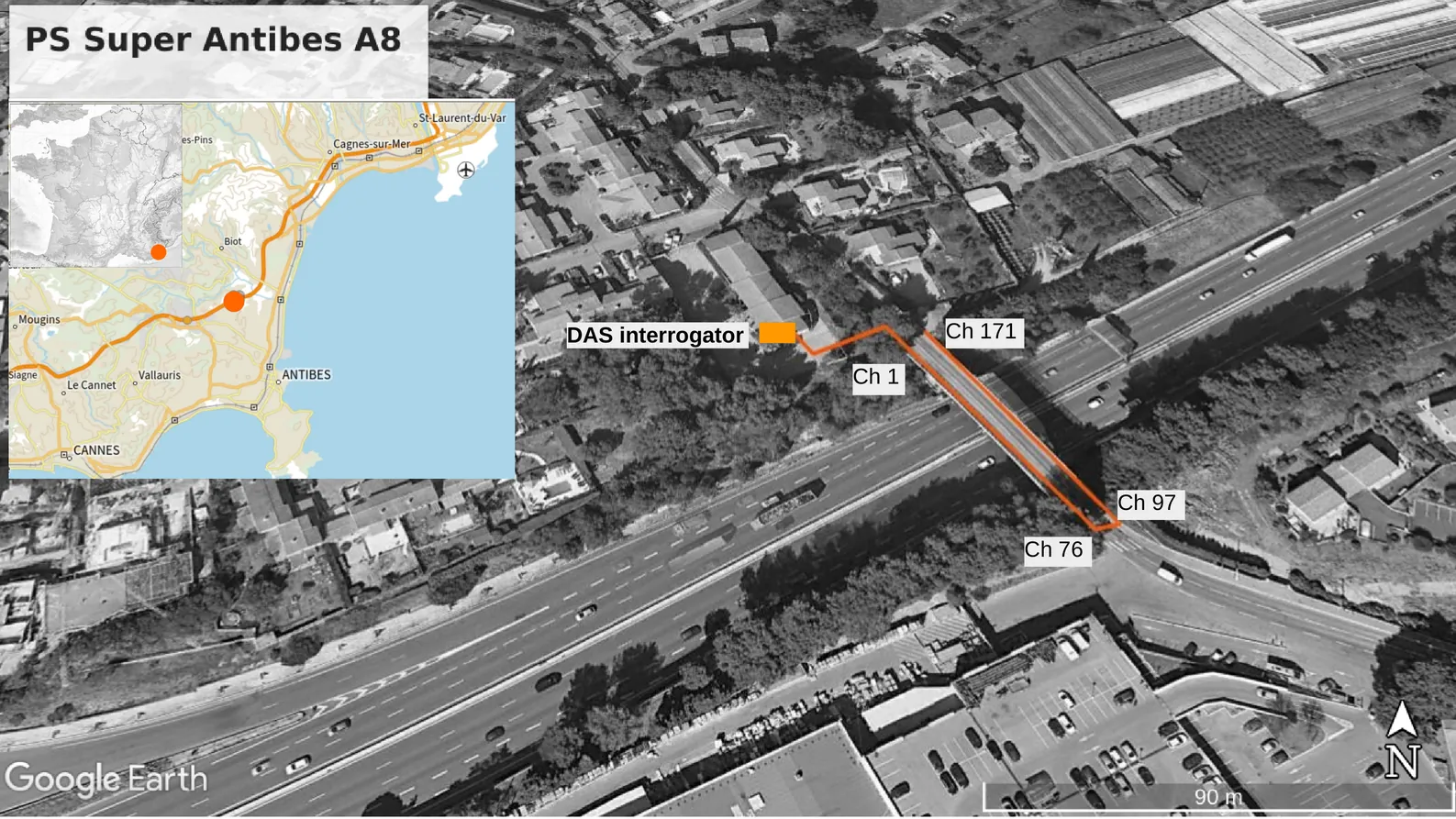
Distributed Acoustic Sensing (DAS) of ambient vibrations is a promising technique in the context of structural health monitoring of civil engineering structures. The methodology uses Rayleigh backscattered light from small deformations at different locations of the sensed fiber-optic cable, turning it into a large array of equally distributed strain sensors. In this paper, we demonstrate the feasibility of using DAS technology to record dynamic strain used for modal identification through the Operational Modal Analysis (OMA) of a strut-frame bridge overpassing the A8 highway in southeastern France. Modal identification using DAS data is successful despite its predominantly axial sensitivity (along fiber), though the help of three-component seismometers is useful for discriminating the main motion direction of each identified mode. The identification of 1 bridge's normal modes with unprecedented spatial resolution is obtained from the lowest (transverse and longitudinal) modes to high-order modes that present significant vertical motion. In addition, strong seasonal effects are observed in both the absolute frequency values and the modal shapes of the first transverse and longitudinal modes of the bridge, comparing ambient vibration testing and DAS surveys carried out in the summer and winter periods.
A special 2D initial conditions' domain of the equal-mass zero angular momentum planar three-body problem, which has been formerly studied, is analyzed to deepen the knowledge of the stability regions in it. The decay times in the domain are carefully computed. Four stability regions are established. 971 verified initial conditions for linearly stable periodic collisionless orbits are found. Many of these identified initial conditions are new ones. The periodic orbits of each stability region are characterized by a certain pattern in their syzygy sequences. Additional computations show that the orbits found should be considered as candidates for KAM-stable orbits.
 2511.01889
2511.01889The model of magnetic monopoles that was proposed by Paul Dirac in 1931 has long been a subject of theoretical interest in physics because of its potential to explain the quantization of electric charge. While much attention has been given to non-Dirac monopoles, Dirac's model, which involves an infinitely thin solenoid known as a Dirac string, presents subtleties in the interaction between monopoles. In this paper, we show that the force between two Dirac monopoles obeys a Coulomb-like interaction law. This derivation offers an instructive exercise in fundamental electromagnetism concepts and is appropriate for undergraduate and early graduate-level students.
Mechanical energy is lost to friction during a shot with a trebuchet. The losses are mainly due to sliding friction at the bearings for the throwing arm and at the hinge for the swinging counterweight, but the aerodynamic force on the sling also contributes. Generalized forces for these sliding and aerodynamic frictions are derived and included in the equations for the internal movement of the engine. The equations are solved by the use of perturbation theory and calculated losses are compared with results from an experimental engine of small dimensions. Scaling to full-size trebuchets is discussed.
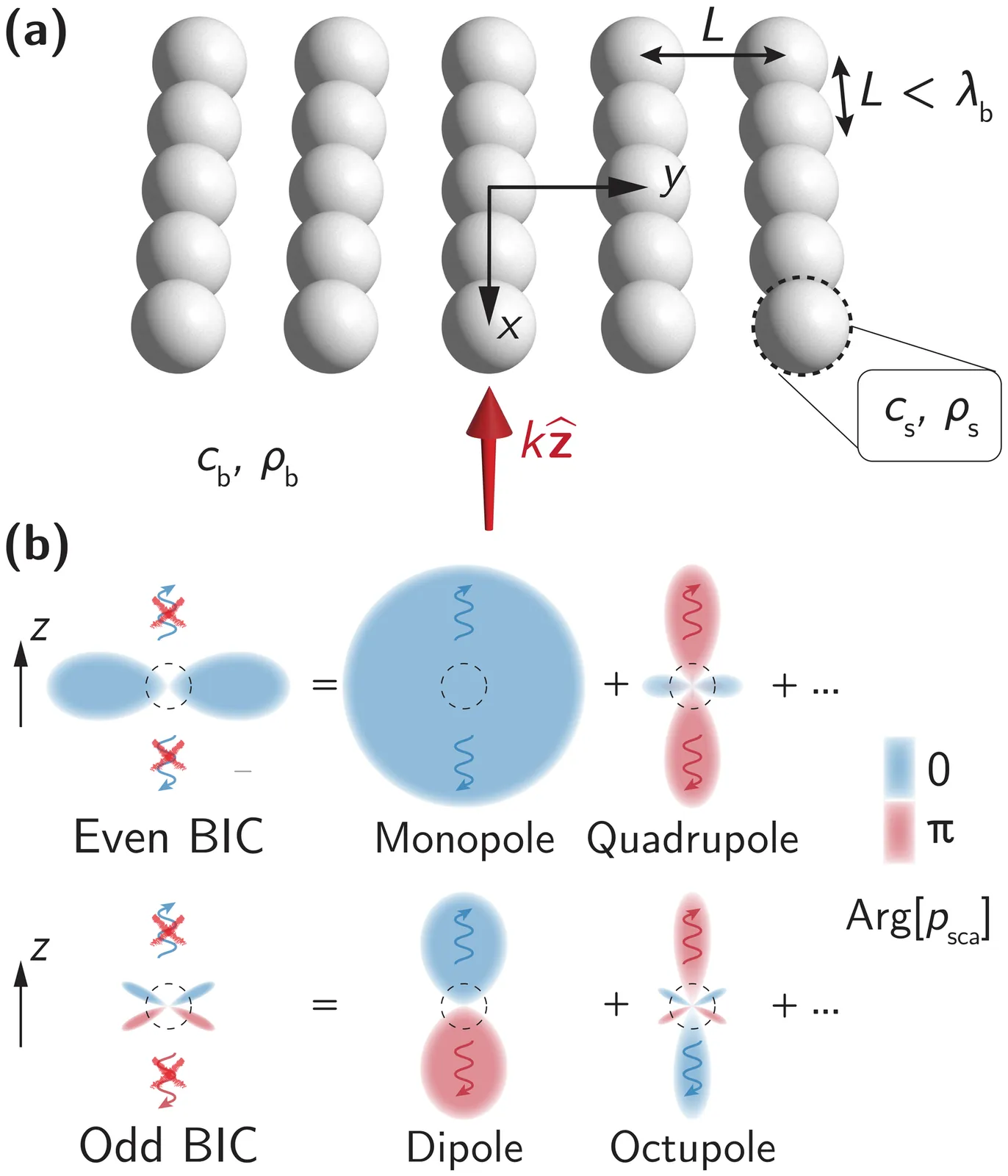
A referential example of a physical system that supports bound states in the continuum (BICs) with an infinite quality factor ($Q$-factor) is a subwavelength lattice of discrete scatterers (resonators) whose response can be significantly modified by exploiting lattice interactions. In this work, we explore the multipole interference mechanism for realizing accidental acoustic BICs (trapped modes) at the $Γ$-point (in-plane Bloch wave vector $\mathbf{k}_{\parallel} = \mathbf{0}$) in biperiodic lattices of acoustic resonators with one resonator per unit cell. To do so, we expand the pressure field from the lattice into a series of scalar zonal ($m = 0$) spherical multipoles, carried by a normally incident plane wave, and formulate analytical conditions on the resonator's multipole moments under which an eigenmode becomes a BIC. The conditions allow us to determine the lattice constant and frequency values that enable the formation of the axisymmetric BIC due to the destructive interference of radiation from zonal multipole moments of a certain parity, although each moment radiates individually. By employing the T-matrix method for acoustic metasurfaces, we numerically investigate the BIC resonance in various structures, including finite arrays, and also the transformation of such resonances into high-$Q$ quasi-BIC regimes, which can be excited by a plane wave at normal incidence.
 2510.17054
2510.17054An outline is given of the derivation of two inhomogeneous wave equations in an influential 2002 AJP paper of Jackson on the transformation from the Lorenz gauge to other electromagnetic gauges. The derivation shows that, contrary to a statement in the paper, the function satisfying one of the equations is not associated with the Coulomb-gauge vector potential but is associated with the Lorenz-gauge vector potential instead.