Populations and Evolution
Population dynamics, spatio-temporal patterns, evolution, co-evolution, biodiversity, phylogeny, models of epidemics.
Population dynamics, spatio-temporal patterns, evolution, co-evolution, biodiversity, phylogeny, models of epidemics.
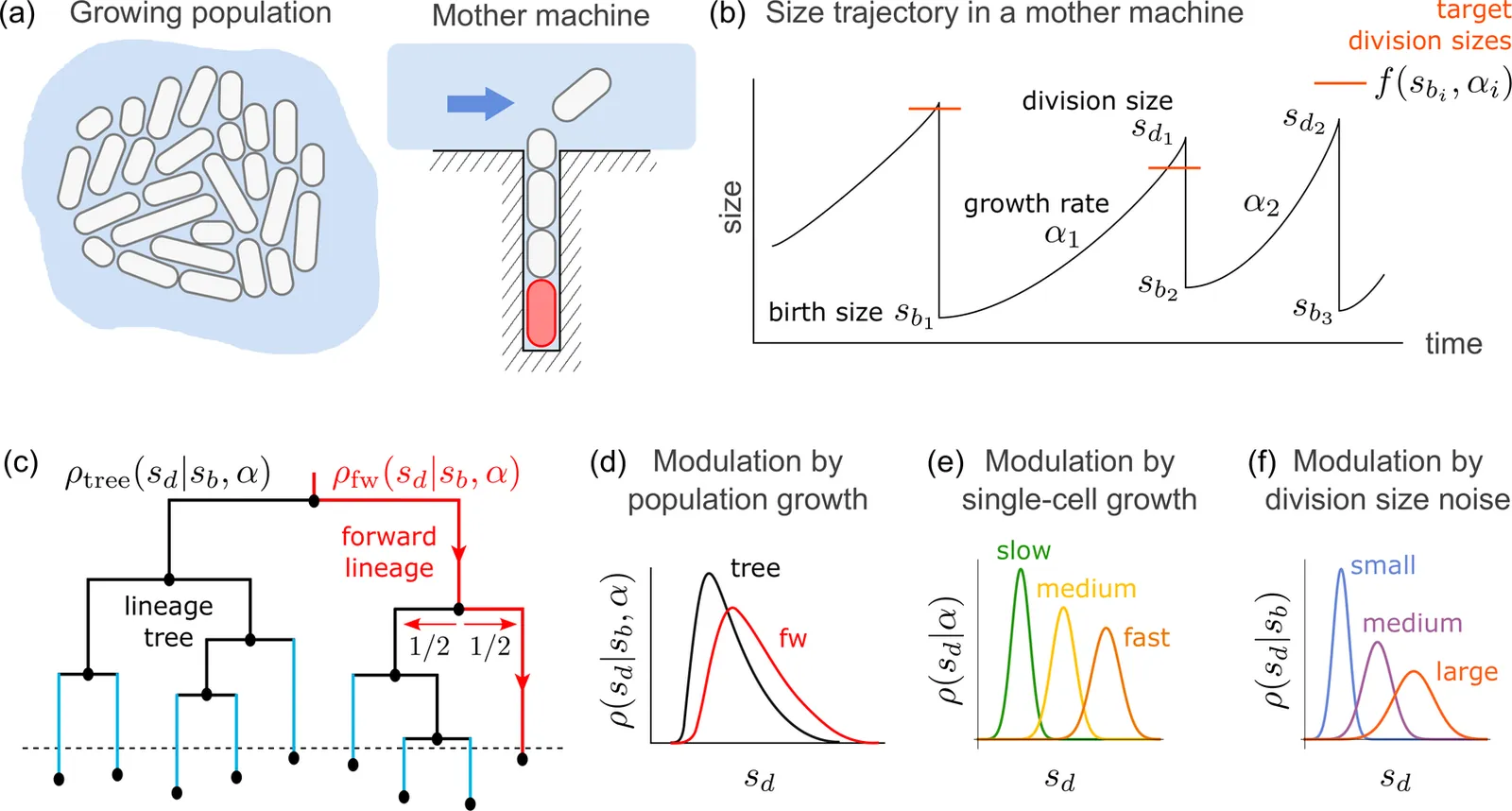
Living cells maintain size homeostasis by actively compensating for size fluctuations. Here, we present two stochastic maps that unify phenomenological models by integrating fluctuating single-cell growth rates and size-dependent noise mechanisms with cell size control. One map is applicable to mother machine lineages and the other to lineage trees of exponentially-growing cell populations, which reveals that population dynamics alter size control measured in mother machine experiments. For example, an adder can become more sizer-like or more timer-like at the population level depending on the noise statistics. Our analysis of bacterial data identifies extrinsic noise as the dominant mechanism of size variability, characterized by a quadratic conditional variance-mean relationship for division size across growth conditions. This finding contradicts the reported independence of added size relative to birth size but is consistent with the adder property in terms of the independence of the mean added size. Finally, we derive a trade-off between population-growth-rate gain and division-size noise. Correlations between size control quantifiers and single-cell growth rates inferred from data indicate that bacteria prioritize a narrow division-size distribution over growth rate maximisation.
 2601.04325
2601.04325We explore the connection between evolution and large-deviation theory. To do so, we study evolutionary dynamics in which individuals experience mutations, reproduction, and selection using variants of the Moran model. We show that, in the large population size limit, the impact of reproduction and selection amounts to realizing a large-deviation dynamics for the non-interacting random walk in which individuals simply explore the genome landscape due to mutations. This mapping, which holds at all times, allows us to recast transitions in the population genome distribution as dynamical phase transitions, which can then be studied using the toolbox of large-deviation theory. Finally, we show that the mapping extends beyond the class of Moran models.
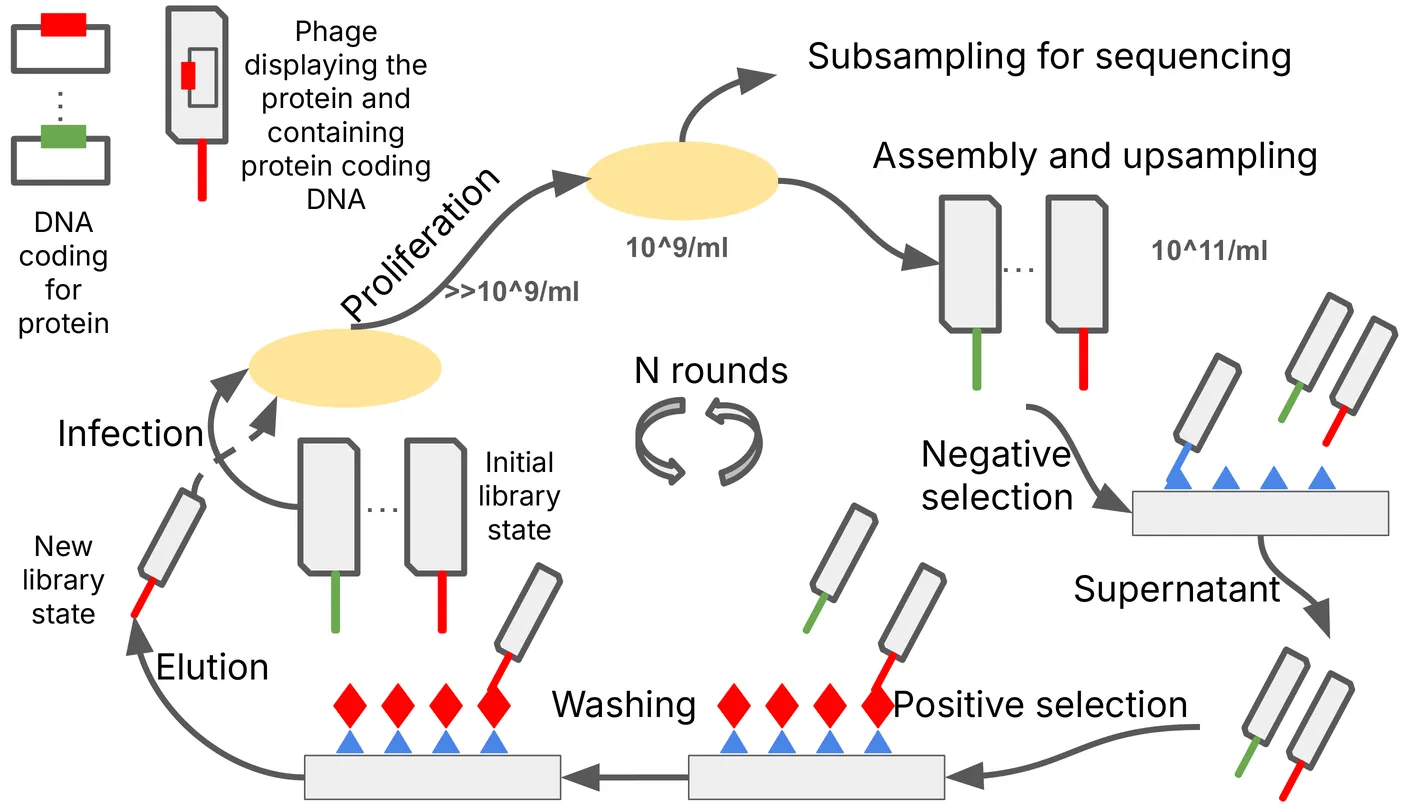
Phage display is a powerful laboratory technique used to study the interactions between proteins and other molecules, whether other proteins, peptides, DNA or RNA. The under-utilisation of this data in conjunction with deep learning models for protein design may be attributed to; high experimental noise levels; the complex nature of data pre-processing; and difficulty interpreting these experimental results. In this work, we propose a novel approach utilising a Bayesian Neural Network within a training loop, in order to simulate the phage display experiment and its associated noise. Our goal is to investigate how understanding the experimental noise and model uncertainty can enable the reliable application of such models to reliably interpret phage display experiments. We validate our approach using actual binding affinity measurements instead of relying solely on proxy values derived from 'held-out' phage display rounds.
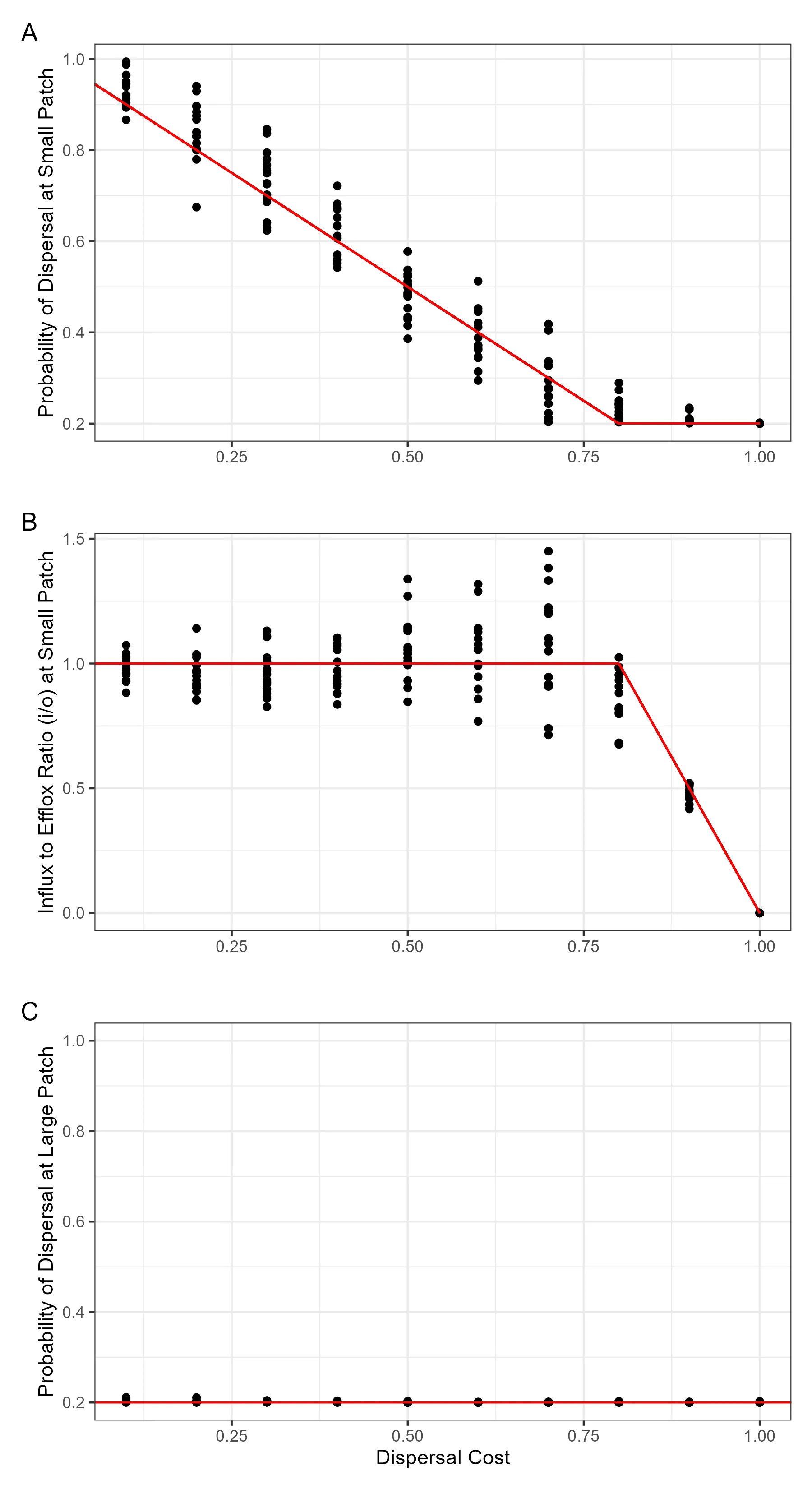
Fitness consequence of dispersal depends on property of the entire landscape, which patches are available and what are the cost of moving. These are information that are not available locally when an organism make the decision to disperse. This poses a problem to the organism, where it is unclear how an adaptive decision can be made. This also poses a problem to the scientist, since in order to study the adaptiveness of dispersal, we need information of the entire landscape. For theorist, this is through making a series of assumption about either the landscape or the organism, and for empiricists, this means a large amount of measurements needs to be made across a large area. In this paper, we propose a link between local demographic process, which an organism can have access to, to the fitness consequence of dispersal. This meant local environmental cue can be used for the decision on dispersal, and hence allow the evolution of plastic dispersal strategy. We will then show that using this approach, evolution of dispersal on complex landscape can be modelled with relative ease, and to show that accidental dispersal in one patch can drive the evolution of adaptive dispersal in another.
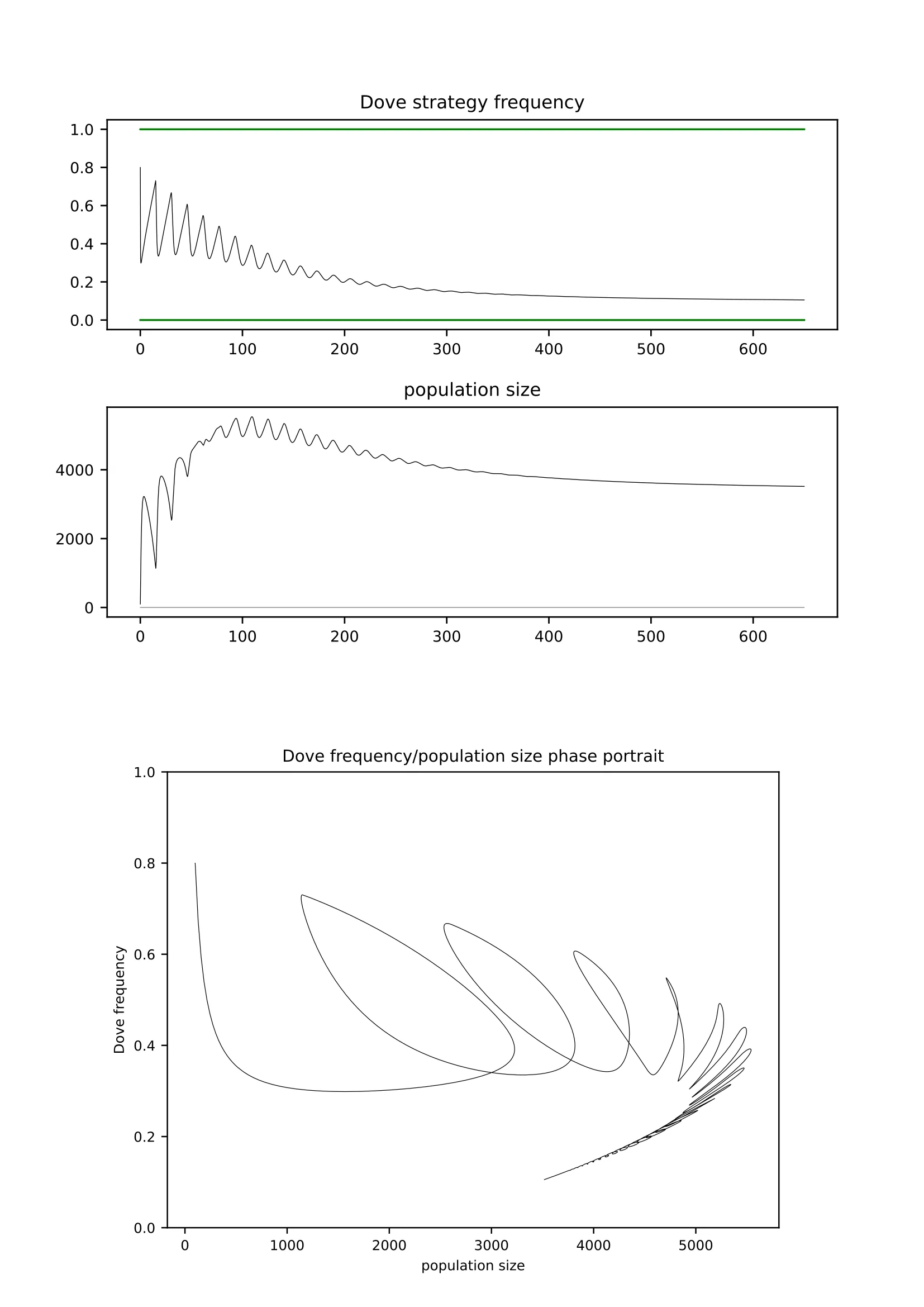
In this paper, we extend the demographic eco-evolutionary game approach, based on explicit birth and death dynamics instead of abstract "fitness" interpreted as an abstract "Malthusian parameter", by the introduction of the delay resulting from the juvenile maturation time. This leads to the application of the Delay Differential Equations (DDE). We show that delay seriously affects the resulting dynamics and may lead to the loss of stability of equilibria when critical delay is exceeded. We provide theoretical tools for the assessment of the critical delays and the parameter values when this may happen. Our results emphasize the importance of the mechanisms of density dependence. We analyze the impact of three different suppression modes based on: adult mortality, juvenile recruitment survival after the maturation period (without delay), and juvenile recruitment at birth (with the delay). The last mode leads to extreme patterns such as bifurcations, complex cycles, and chaotic dynamics. However, surprisingly, this mode leads to extension of the duration of the temporary transient metastable states known as "ghost attractors". In addition, we also focus on the problem of resilience of the analyzed systems against external periodic perturbations and feedback-driven factors such as additional predator pressure.
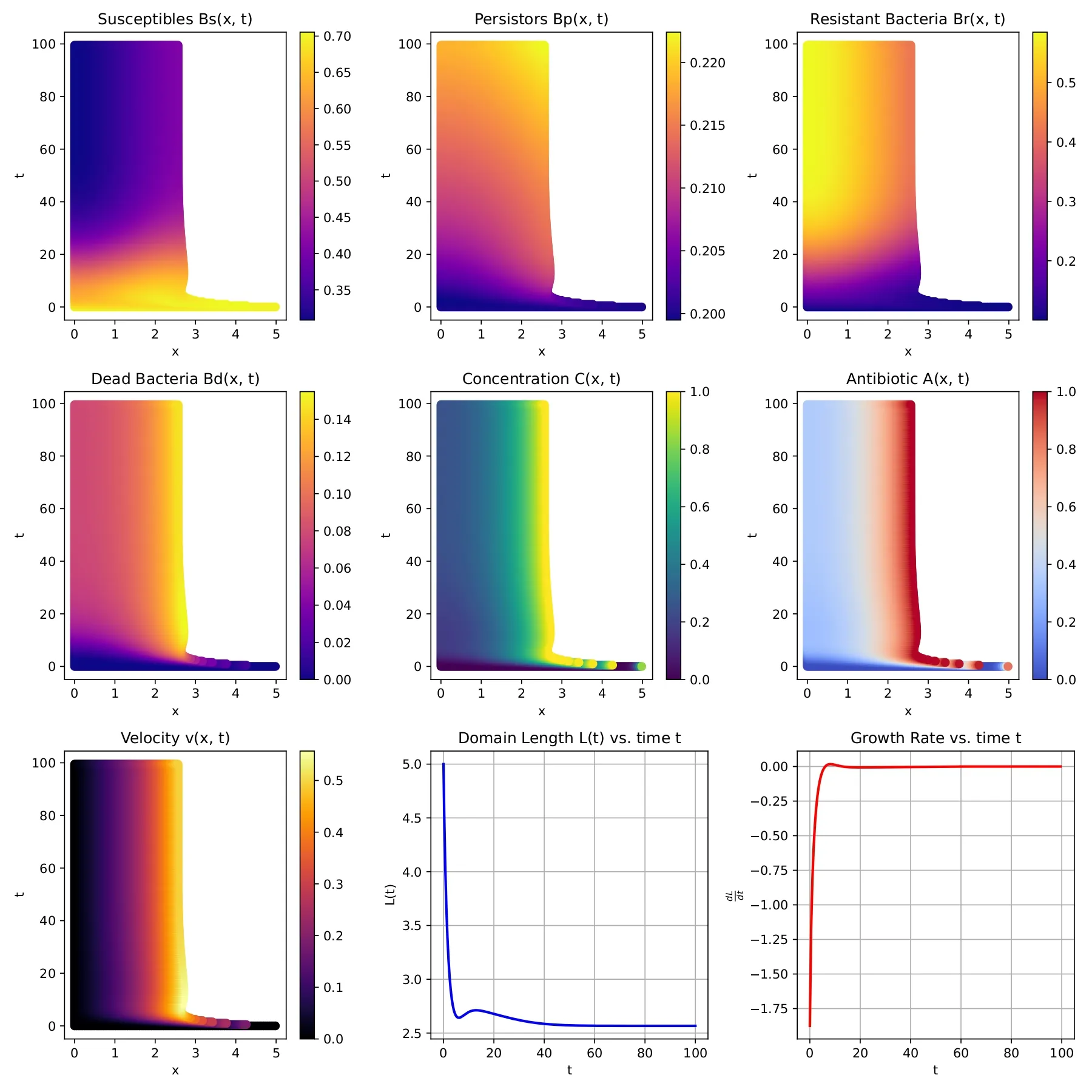
We propose and analyze a model for antibiotic resistance transfer in a bacterial biofilm and examine antibiotic dosing strategies that are effective in bacterial elimination. In particular, we consider a 1-D model of a biofilm with susceptible, persistor and resistant bacteria. Resistance can be transferred to the susceptible bacteria via horizontal gene transfer (HGT), specifically via conjugation. We analyze some basic properties of the model, determine the conditions for existence of disinfection and coexistence states, including boundary equilibria and their stability. Numerical simulations are performed to explore different modeling scenarios and support our theoretical findings. Different antibiotic dosing strategies are then studied, starting with a continuous dosing; here we note that high doses of antibiotic are needed for bacterial elimination. We then consider periodic dosing, and again observe that insufficient levels of antibiotic per dose may lead to treatment failure. Finally, using an extended version of Pontryagin's maximum principle we determine efficient antibiotic dosing protocols, which ensure bacterial elimination while keeping the total dosing low; we note that this involves a tapered dosing which reinforces results presented in other clinical and modeling studies. We study the optimal dosing for different parameter values and note that the optimal dosing schedule is qualitatively robust.

We investigate a type of lunar calendar known as lists of the 'nights of the moon', found throughout East Polynesia, including Rapa Nui (Easter Island). Using computational methods, we analyzed the lexical and structural divergence of 49 calendric lists from all major archipelagos, each containing about 30 night names. Our results, presented as a rooted phylogenetic tree, show a clear split into two main groups: one including lists from Rapa Nui, Mangareva, and the Marquesas; the other comprising lists from New Zealand, Hawaii, the Cook Islands, the Austral Islands, Tahiti, and the Tuamotu. This pattern aligns with a recent alternative classification of East Polynesian languages into 'Distal' (Marquesan, Mangarevan, Rapanui) and 'Proximal' (Maori, Hawaiian, Tahitian, etc.) subgroups. Since both language and lunar calendars are symbolic systems passed down and changed within communities - and given the geographic isolation of many archipelagos - we interpret this correspondence as evidence that the early divergence of East Polynesian lunar calendars mirrors early population movements and language splits in the region.
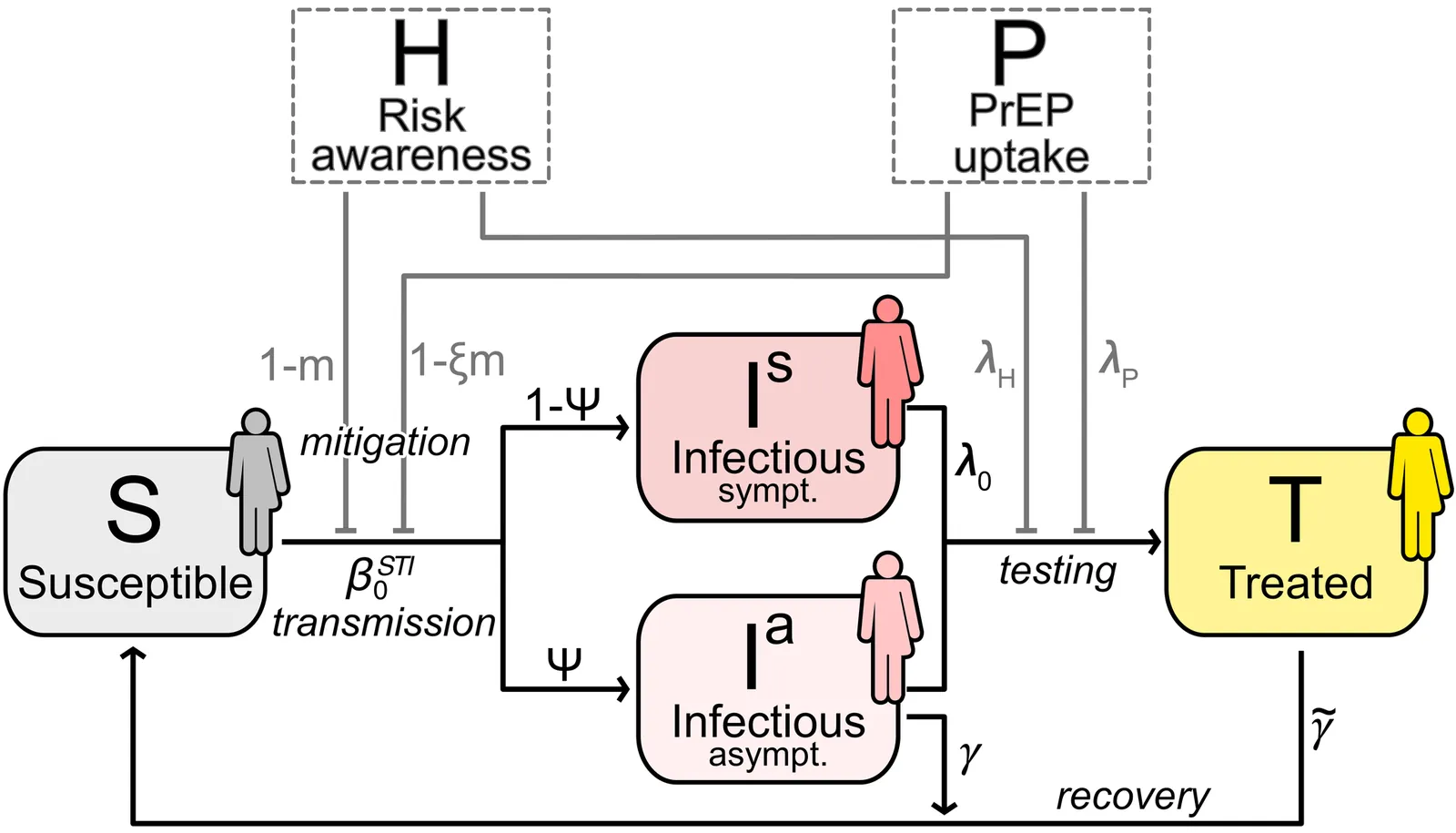
HIV pre-exposure prophylaxis (PrEP) drastically reduces the risk of HIV infection if taken as prescribed, providing almost perfect protection even during unprotected sexual intercourse. Although this has been transformative in reducing new HIV infections among high-risk populations, it has also been linked to an increase in risk practices -- a phenomenon known as risk compensation -- thereby favoring the spread of other sexually transmitted infections (STIs) deemed less severe. In this paper, we study a minimal compartmental model describing the effect of risk awareness and risk compensation due to PrEP on the spread of other STIs among a high-infection-risk group of men who have sex with men (MSM). The model integrates three key elements of risk-mediated behavior and PrEP programs: (i) HIV risk awareness drives self-protective behaviors (such as condom use and voluntary STI screening); (ii) individuals on PrEP are subject to risk compensation, but (iii) are required to screen for asymptomatic STIs frequently. We derived the basic reproduction number of the system, $R_0$, and found a transcritical bifurcation at $R_0=1$, where the disease-free equilibrium becomes unstable and an endemic equilibrium emerges. This endemic equilibrium is asymptotically stable wherever it exists. We identified critical thresholds in behavioral and policy parameters that separate these regimes and analyzed typical values for plausible parameter choices. Beyond the specific epidemiological context, the model serves as a general framework for studying nonlinear interactions between behavioral adaptation, preventive interventions, and disease dynamics, providing insights into how feedback mechanisms can lead to non-trivial responses in epidemic systems. Finally, our model can be easily extended to study the effect of interventions and risk compensation in other STIs.
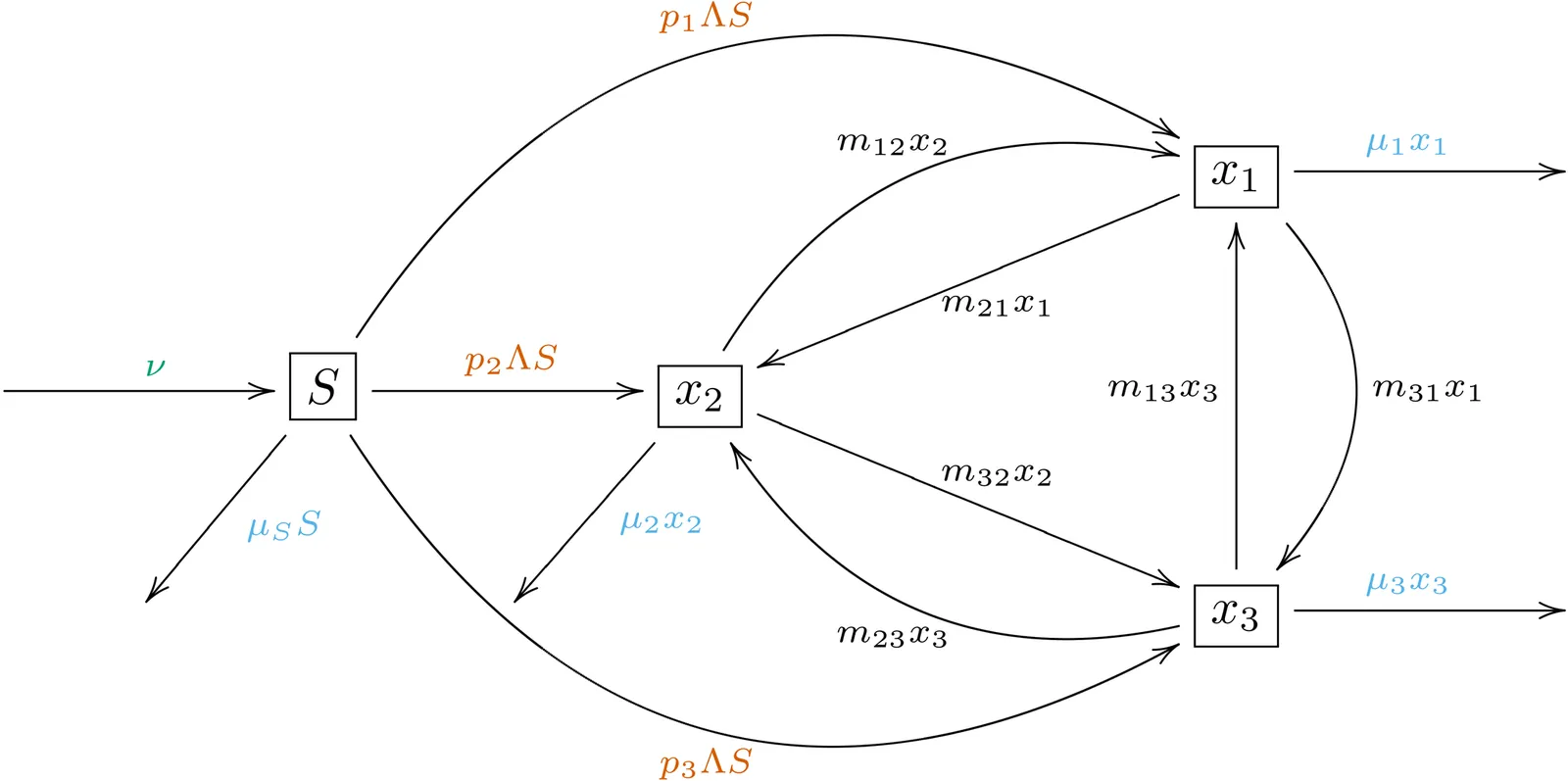
Transmission dynamics of infectious diseases are often studied using compartmental mathematical models, which are commonly represented as systems of autonomous ordinary differential equations. A key step in the analysis of such models is to identify equilibria and find conditions for their stability. Local stability analysis reduces to a problem in linear algebra, but there is no general algorithm for establishing global stability properties. Substantial progress on global stability of epidemic models has been made in the last 20 years, primarily by successfully applying Lyapunov's method to specific systems. Here, we show that any compartmental epidemic model in which susceptible individuals cannot be distinguished and can be infected only once, has a globally asymptotically stable (GAS) equilibrium. If the basic reproduction number ${R}_0$ satisfies ${R}_0 > 1$, then the GAS fixed point is an endemic equilibrium (i.e., constant, positive disease prevalence). Alternatively, if ${R}_0 \le 1$, then the GAS equilibrium is disease-free. This theorem subsumes a large number of results published over the last century, strengthens most of them by establishing global rather than local stability, avoids the need for any stability analyses of these systems in the future, and settles the question of whether co-existing stable solutions or non-equilibrium attractors are possible in such models: they are not.
Community science observational datasets are useful in epidemiology and ecology for modeling species distributions, but the heterogeneous nature of the data presents significant challenges for standardization, data quality assurance and control, and workflow management. In this paper, we present a data workflow for cleaning and harmonizing multiple community science datasets, which we implement in a case study using eBird, iNaturalist, GBIF, and other datasets to model the impact of highly pathogenic avian influenza in populations of birds in the subantarctic. We predict population sizes for several species where the demographics are not known, and we present novel estimates for potential mortality rates from HPAI for those species, based on a novel aggregated dataset of mortality rates in the subantarctic.
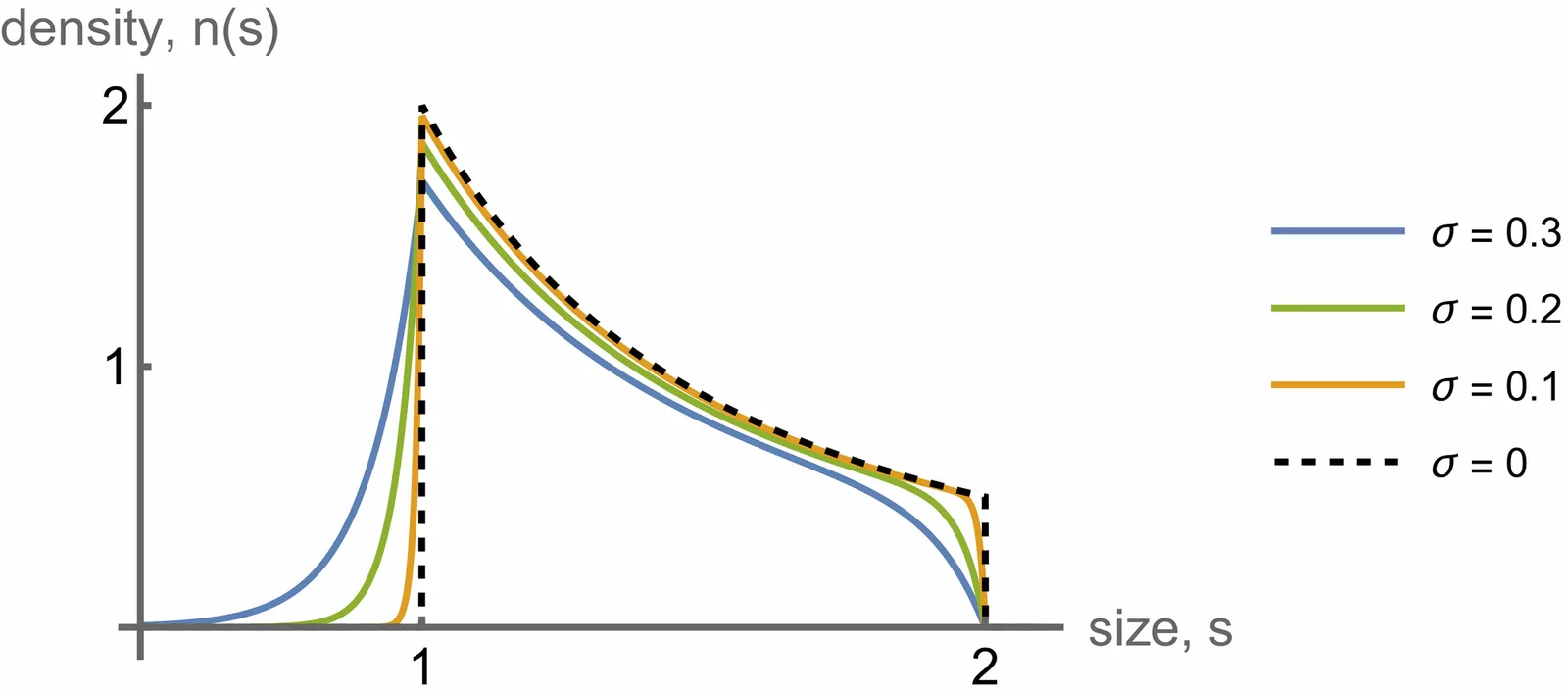
We analyze a size-structured branching process in which individual cells grow exponentially according to a Feller square-root process and divide under general size-control mechanisms. We obtain exact expressions for the asymptotic population growth rate, the steady-state snapshot distribution of cell sizes, and the fluctuations of the total cell number. Our first result is that the population growth rate is exactly equal to the mean single-cell growth rate, for all noise strengths and for all division and size-regulation schemes that maintain size homeostasis. Thus square-root growth noise is neutral with respect to long-term fitness, in sharp contrast to models with size-independent stochastic growth rates. Second, we show that the steady-state population cell-size distribution is obtained from the deterministic inverse-square-law solution by a one-sided exponential convolution with kernel width set by the strength of growth fluctuations. Third, the mean-rescaled population size $N_t/\left\langle N_t\right\rangle$ converges to a stationary compound Poisson-exponential distribution that depends only on growth noise. This distribution, and hence the long-time shape of population-size fluctuations, is unchanged by division-size noise or asymmetric partitioning. These results identify Feller-type exponential growth with square-root noise as an exactly solvable benchmark for stochastic growth in size-controlled populations and provide concrete signatures that distinguish it from models with size-independent growth-rate noise.

This study presents an agent-based model (ABM) developed to simulate staff and resident interactions within a synthetic aged care facility, capturing movement, task execution, and proximity-based contact events across three staff shifts and varying levels of resident care. Contacts were defined by spatial thresholds (1.5 m and 3 m) and cumulative duration, enabling the generation of detailed contact matrices. Simulation results showed that low and medium care residents experienced the highest frequency of interactions, particularly with staff on morning and afternoon shifts, while high care residents and night staff had substantially fewer contacts. Contact rates varied significantly by care level and shift, confirmed through Poisson-based regression modelling. Temporal analyses revealed clustering of high-risk contacts during structured daily routines, especially communal and care activities. An integrated airborne transmission module, seeded with a single infectious staff member, demonstrated that infection risk was highest during high-contact shifts and among medium care residents. Vaccination scenarios reduced predicted transmission by up to 68\%, with the greatest impact observed when both staff and residents were vaccinated. These findings highlight the importance of accounting for contact heterogeneity in aged care and demonstrate the utility of ABMs for evaluating targeted infection control strategies in high-risk, enclosed environments.
Large animal groups -- bird flocks, fish schools, insect swarms -- are often assumed to form by gradual aggregation of sparsely distributed individuals. Using a mathematically precise framework based on time-varying directed interaction networks, we show that this widely held view is incomplete. The theory demonstrates that large moving groups do not arise by slow accumulation; instead, they emerge through the rapid merging of multiple pre-existing subgroups that are simultaneously activated under high-density conditions. The key mechanism is topological: the long-term interaction structure of any moving group contains a single dominant strongly connected component (SCC). This dominant SCC determines the collective velocity -- both speed and direction -- of the entire group. When two subgroups encounter one another, the trailing subgroup aligns with -- and ultimately inherits -- the velocity of the dominant SCC of the leading subgroup. Repeated merging events naturally generate large groups whose speed is predicted to be lower than the mean speed of the original subgroups. The same dynamics explain several universal empirical features: broad neighbour-distance distributions, directional asymmetry in neighbour selection, and the characteristic narrow-front, wide-rear geometry of real flocks. The framework yields testable predictions for STARFLAG-style 3D datasets, offering a unified explanation for the formation, maintenance, and geometry of coordinated animal groups.
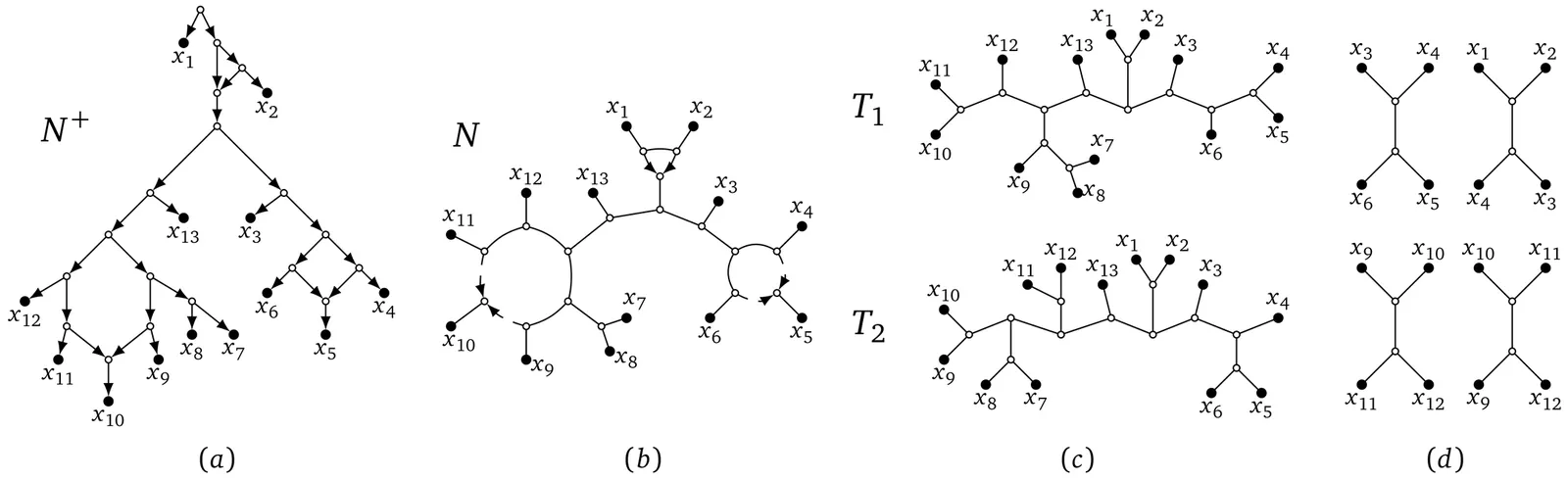
Phylogenetic trees and networks are graphs used to model evolutionary relationships, with trees representing strictly branching histories and networks allowing for events in which lineages merge, called reticulation events. While the question of data sufficiency has been studied extensively in the context of trees, it remains largely unexplored for networks. In this work we take a first step in this direction by establishing bounds on the amount of genomic data required to reconstruct binary level-$1$ semi-directed phylogenetic networks, which are binary networks in which reticulation events are indicated by directed edges, all other edges are undirected, and cycles are vertex-disjoint. For this class, methods have been developed recently that are statistically consistent. Roughly speaking, such methods are guaranteed to reconstruct the correct network assuming infinitely long genomic sequences. Here we consider the question whether networks from this class can be uniquely and correctly reconstructed from finite sequences. Specifically, we present an inference algorithm that takes as input genetic sequence data, and demonstrate that the sequence length sufficient to reconstruct the correct network with high probability, under the Cavender-Farris-Neyman model of evolution, scales logarithmically, polynomially, or polylogarithmically with the number of taxa, depending on the parameter regime. As part of our contribution, we also present novel inference rules for quartet data in the semi-directed phylogenetic network setting.

We considered a model for an infectious disease outbreak, when the depletion of susceptible individuals is negligible, and assumed that individuals adapt their behavior according to the information they receive about new cases. In line with the information index approach, we supposed that individuals react to past information according to a memory kernel that is continuously distributed in the past. We analyzed equilibria and their stability, with analytical results for selected cases. Thanks to the recently developed pseudospectral approximation of delay equations, we studied numerically the long-term dynamics of the model for memory kernels defined by gamma distributions with a general non-integer shape parameter, extending the analysis beyond what is allowed by the linear chain trick. In agreement with previous studies, we showed that behavior adaptation alone can cause sustained waves of infections even in an outbreak scenario, and notably in the absence of other processes like demographic turnover, seasonality, or waning immunity. Our analysis gives a more general insight into how the period and peak of epidemic waves depend on the shape of the memory kernel and how the level of minimal contact impacts the stability of the behavior-induced positive equilibrium.
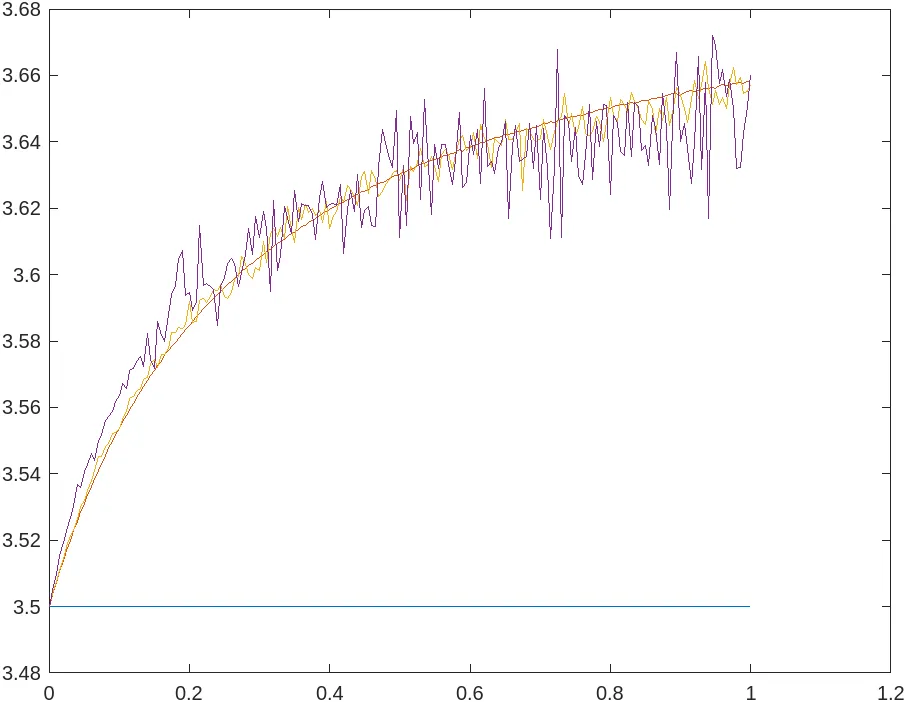
We look at the interaction of dispersal and environmental stochasticity in $n$-patch models. We are able to prove persistence and extinction results even in the setting when the dispersal rates are stochastic. As applications we look at Beverton-Holt and Hassell functional responses. We find explicit approximations for the total population size at stationarity when we look at slow and fast dispersal. In particular, we show that if dispersal is small then in the Beverton-Holt setting, if the carrying capacity is random, then environmental fluctuations are always detrimental and decrease the total population size. Instead, in the Hassell setting, if the inverse of the carrying capacity is made random, then environmental fluctuations always increase the population size. Fast dispersal can save populations from extinction and therefore increase the total population size. We also analyze a different type of environmental fluctuation which comes from switching environmental states according to a Markov chain and find explicit approximations when the switching is either fast or slow - in examples we are able to show that slow switching leads to a higher population size than fast switching. Using and modifying some approximation results due to Cuello, we find expressions for the total population size in the $n=2$ patch setting when the growth rates, carrying capacities, and dispersal rates are influenced by random fluctuations. We find that there is a complicated interaction between the various terms and that the covariances between the various random parameters (growth rate, carrying capacity, dispersal rate) play a key role in whether we get an increase or a decrease in the total population size. Environmental fluctuations turn to sometimes be beneficial -- this show that not only dispersal, but also environmental stochasticity can lead to an increase in population size.
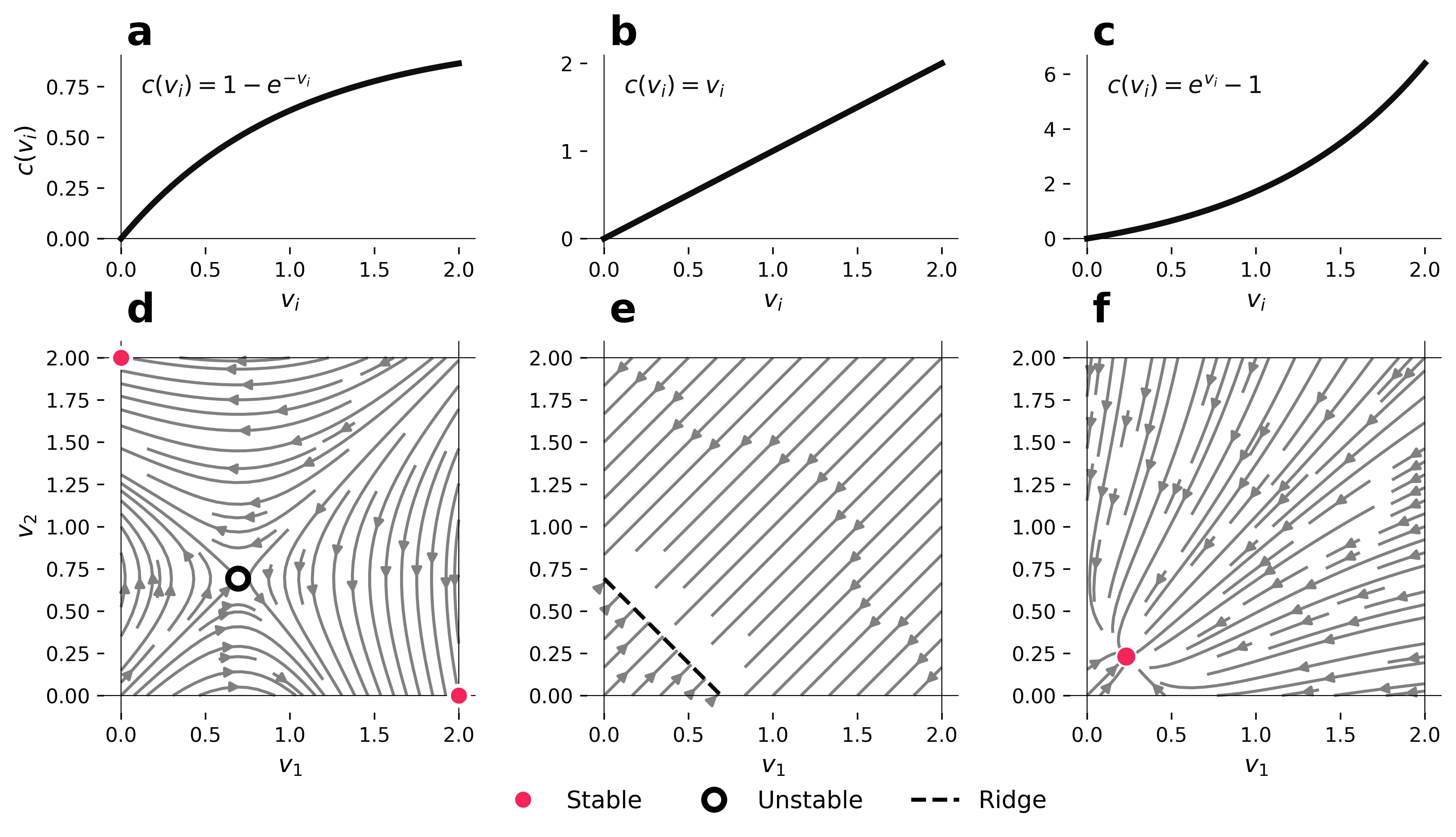
Collective vigilance describes how animals in groups benefit from the predator detection efforts of others. Empirical observations typically find either a many-eyes strategy with all (or many) group members maintaining a low level of individual vigilance, or a sentinel strategy with one (or a few) individuals maintaining a high level of individual vigilance while others do not. With a general analytical treatment that makes minimal assumptions, we show that these two strategies are alternate solutions to the same adaptive problem of balancing the costs of predation and vigilance. Which strategy is preferred depends on how costs scale with the level of individual vigilance: many-eyes strategies are preferred where costs of vigilance rise gently at low levels but become steeper at higher levels (convex; e.g. an open field); sentinel strategies are preferred where costs of vigilance rise steeply at low levels and then flatten out (concave; e.g. environments with vantage points). This same dichotomy emerges whether individuals act selfishly to optimise their own fitness or cooperatively to optimise group fitness. The model is extended to explain discrete behavioural switching between strategies and differential levels of vigilance such as edge effects.
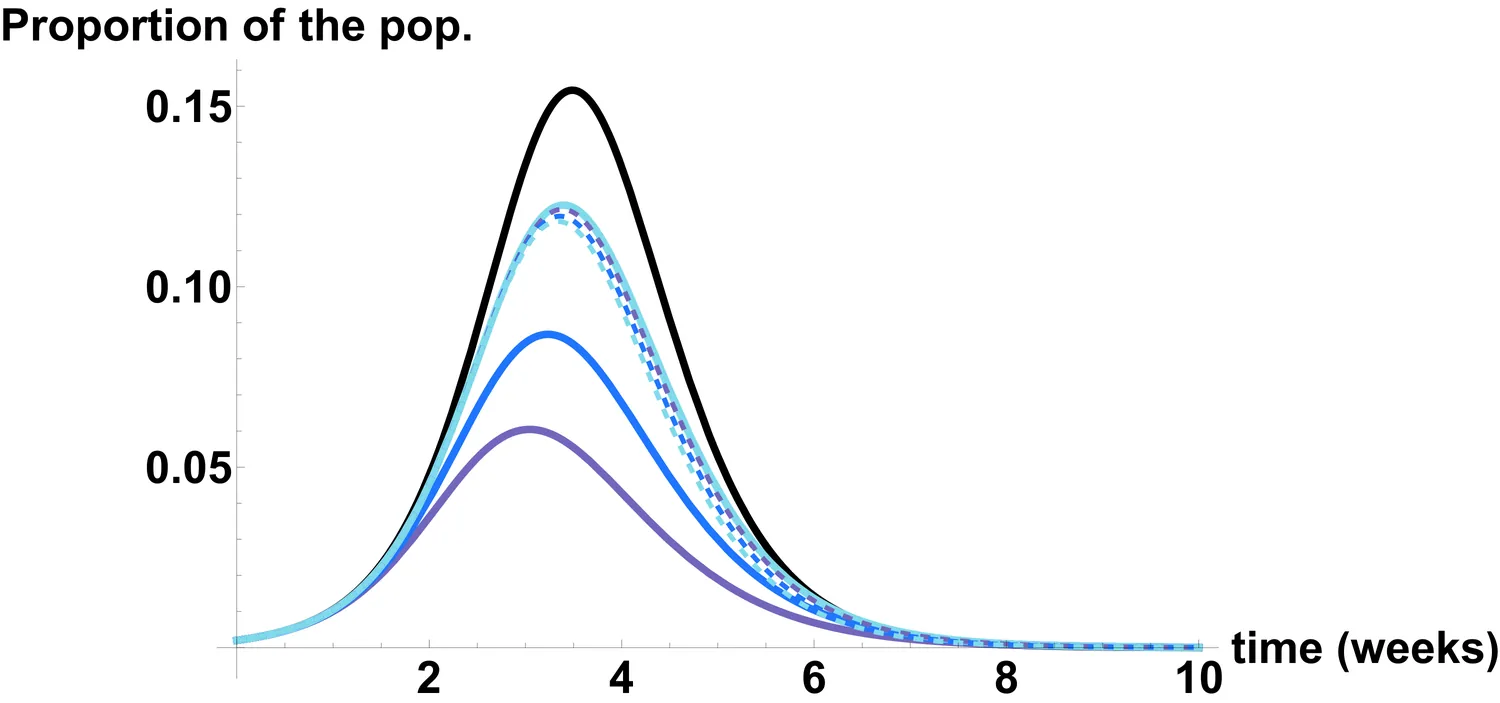
Population heterogeneity is a key factor in epidemic dynamics, influencing both transmission and final epidemic size. While heterogeneity is often modeled through age structure, spatial location, or contact patterns, differences in host susceptibility have recently gained attention, particularly during the COVID-19 pandemic. Building on the framework of Diekmann and Inaba (Journal of Mathematical Biology, 2023), we focus on the special case of SEIR-models, which are widely used for influenza and other respiratory infections. We derive the model equations under two distinct assumptions linking susceptibility and infectiousness. Analytical results show that heterogeneity in susceptibility reduces the epidemic final size compared to homogeneous models with the same basic reproduction number $\Ro$. In the case of gamma-distributed susceptibility, we obtain stronger results on the epidemic final size. The resulting model captures population heterogeneity through a single parameter, which makes it practical for fitting epidemic data. We illustrate its use by applying it to seasonal influenza in Italy.
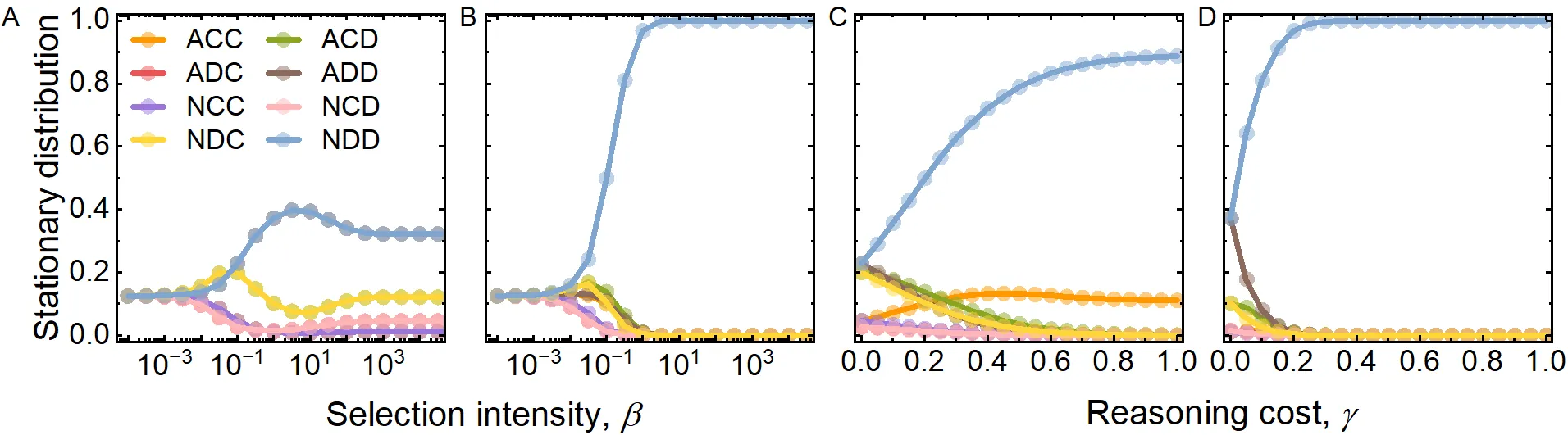
Understanding how cooperation emerges and persists is a central challenge in evolutionary game theory. Existing models often rely on restricted, hand-picked strategy sets, which can overlook critical behavioural pathways. A recent four-strategy framework showed that cheap talk can promote cooperation through local interactions, yet it remained unclear whether modelled strategies might alter these conclusions. Here, we extend this framework to the complete set of eight strategies that naturally arise from communication and decision-making rules. We show that incorporating the full strategy space dramatically changes the evolutionary landscape. Cooperation becomes both more robust and more versatile, driven by novel pathways absent in the restricted model. In particular, we uncover a previously overlooked mechanism in which suspicious cooperation catalyses a cyclic dynamic that sustains cooperation. Conversely, the assumed role of strategic defection in the biased model is fragile, acting mainly as a spoiler rather than a genuine evolutionary attractor. The complete model further reveals a rich spectrum of long-term behaviours, including stable coexistence among up to seven strategies and time-varying patterns of partial coexistence. These results demonstrate that the full strategy space unlocks hidden routes to cooperative behaviour and highlight the importance of comprehensive modelling when explaining the emergence of cooperation.
We study a model for a mosquito-borne epidemic outbreak in which humans can adopt protective behaviour against vector bites depending on information on the past and present prevalence. Assuming that mosquitoes can also feed on other non-competent hosts (i.e. hosts that cannot infect others), we first review some results from the literature by showing that protective behaviour may either decrease or increase the value of the reproduction number of the epidemic depending on multiple elements. Then, assuming that changes in opinion occur much faster than the spread of the disease, we exploit an approach based on the Geometric Singular Perturbation Theory to reduce the two-group model to a model for a homogeneous host population. Then, we use the resulting model to investigate the effect of information-induced behavioural changes on the transient dynamics of the epidemic, discussing the case when protective measures induced an outbreak with a low attack rate. We illustrate how behavioural changes might either help in containing an epidemic outbreak or make the epidemic last longer, even triggering recurrent damped epidemic waves. We conclude with numerical simulations to illustrate our analytical results.