Trending in High Energy Physics
Integrable Systems
These notes are based on lecture courses I gave to third year mathematics students at Cambridge. They could form a basis of an elementary one--term lecture course on integrable systems covering the Arnold-Liouville theorem, inverse scattering transform, Hamiltonian methods in soliton theory and Lie point symmetries. No knowledge beyond basic calculus and ordinary differential equation is assumed.
2601.04077
Jan 2026High Energy Physics - Theory
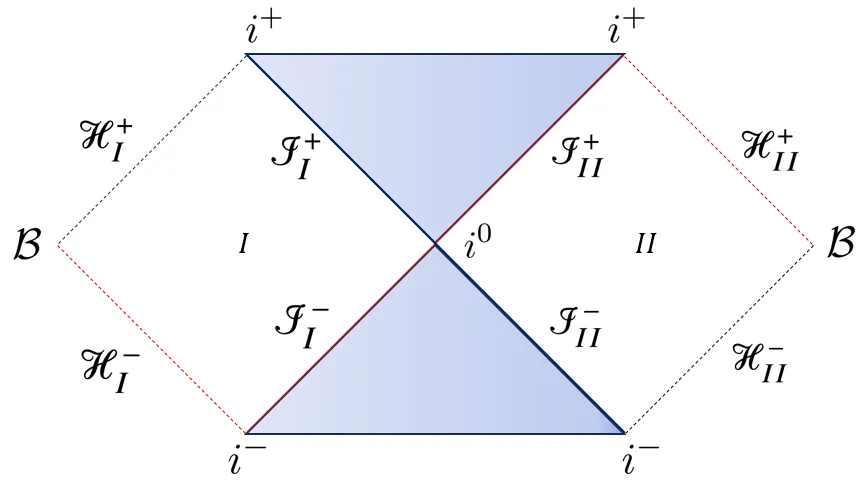
Black hole thermodynamics at null infinity. Part 2: Open systems, Markovian dynamics and work extraction from non-rotating black holes
Black hole thermodynamics provides a unique setting in which general relativity, quantum field theory, and statistical mechanics converge. In semiclassical gravity, this interplay culminates in the generalized second law (GSL), whose modern proofs rely on information theoretic techniques applied to algebras of observables defined on null hypersurfaces. These proofs exhibit close structural parallels with the thermodynamics of open quantum systems governed by Markovian dynamics. In this work, we draw parallels between the dynamics of quantum fields in regions bounded by non expanding causal horizons and the thermodynamics of quantum systems weakly coupled to equilibrium reservoirs. We introduce a dictionary relating late time boundary conditions to the choice of reservoir, vacuum states to fixed points of the dynamics, and modular Hamiltonians to thermodynamic potentials. Building on results from a companion paper on dual generalized second laws at future null infinity, we show that additional terms appearing in the associated thermodynamic potentials admit a natural interpretation as work contributions. We demonstrate that certain non thermal vacuum states at null infinity allow for the operation of autonomous thermal engines and enable work extraction from the radiation. Extending the analysis to the Unruh vacuum in Schwarzschild and Kerr backgrounds, we obtain generalized grand potential type laws incorporating grey body effects and angular momentum fluxes. Altogether, our results clarify the thermodynamic description of black hole dynamics and place it within the broader framework of open quantum thermodynamics.
2601.03356
Jan 2026High Energy Physics - Theory
$2+2=4$
Motivated by the observation that $2+2=4$, we consider four-dimensional $\mathcal{N}=2$ superconformal field theories on $S^2\timesΣ$, turning on a suitable rigid supergravity background. On the one hand, reduction of a four-dimensional theory ${T}$ on a Riemann surface $Σ$ leads to a family $\mathscr{F}[{T}, Σ]$ of two-dimensional $(2,2)$ unitary SCFTs, a two-dimensional analog of the four-dimensional theories of class $\mathscr{S}$. On the other hand, reduction on $S^2$ yields a non-unitary two-dimensional CFT $\mathscr{C}[{T}]$ whose chiral algebra is the same as the one associated to ${T}$ by the standard SCFT/VOA correspondence. This construction upgrades the vertex operator algebra to a full-fledged two-dimensional CFT. What's more, it leads to a novel 2d/2d correspondence, a "$2+2 = 4$" analog of the "$4+2=6$" AGT correspondence: the $S^2$ partition function of $\mathscr{F}[{T}; Σ]$ is computed by correlation functions of $\mathscr{C}[{T}]$ on $Σ$. The elliptic genus of $\mathscr{F}[{T}; Σ]$ is instead computed by a topological QFT $\mathscr{E}[T]$ on $Σ$. A central question is whether one can give a purely two-dimensional presentation of the family $\mathscr{F}[{T}; Σ]$ of $(2, 2)$ theories. We propose an algorithm to realize the $(2, 2)$ theories as gauged linear sigma models when ${T}$ is an Argyres-Douglas theory of type $(A_1, A_{2k})$ and $Σ$ an $n$-punctured sphere. We perform stringent checks of our conjecture for $k=1$ and $k=2$.
2601.00058
Dec 2025High Energy Physics - Theory
 2601.00605
2601.00605Effective field theory for dissipative photons from higher-form symmetries
Recent developments in generalized symmetries have provided new insights into quantum field theories. Within this framework, photons can be understood as Nambu-Goldstone modes associated with a spontaneously broken higher-form symmetry. In this work, we develop an effective field theory that builds on this symmetry structure to describe the real-time dynamics of photons in insulating media at finite temperature. Combining the Schwinger-Keldysh formalism with the generalized coset construction, we formulate a symmetry-based effective action that incorporates both conservative and dissipative effects. The effective theory implements the dynamical Kubo-Martin-Schwinger symmetry, ensuring consistency with the fluctuation-dissipation relation and Onsager's reciprocal relations. Within this framework, we derive the entropy current associated with dissipative photon dynamics and demonstrate the non-negativity of its divergence, in accordance with the second law of thermodynamics. We also clarify the symmetry origin of the gauge redundancy in the unbroken phase within the Schwinger-Keldysh framework, relating it to strong and weak realizations of higher-form symmetries. Our results provide a model-independent effective description of photon dynamics in insulating media at finite temperature.
2601.00605
Jan 2026High Energy Physics - Theory
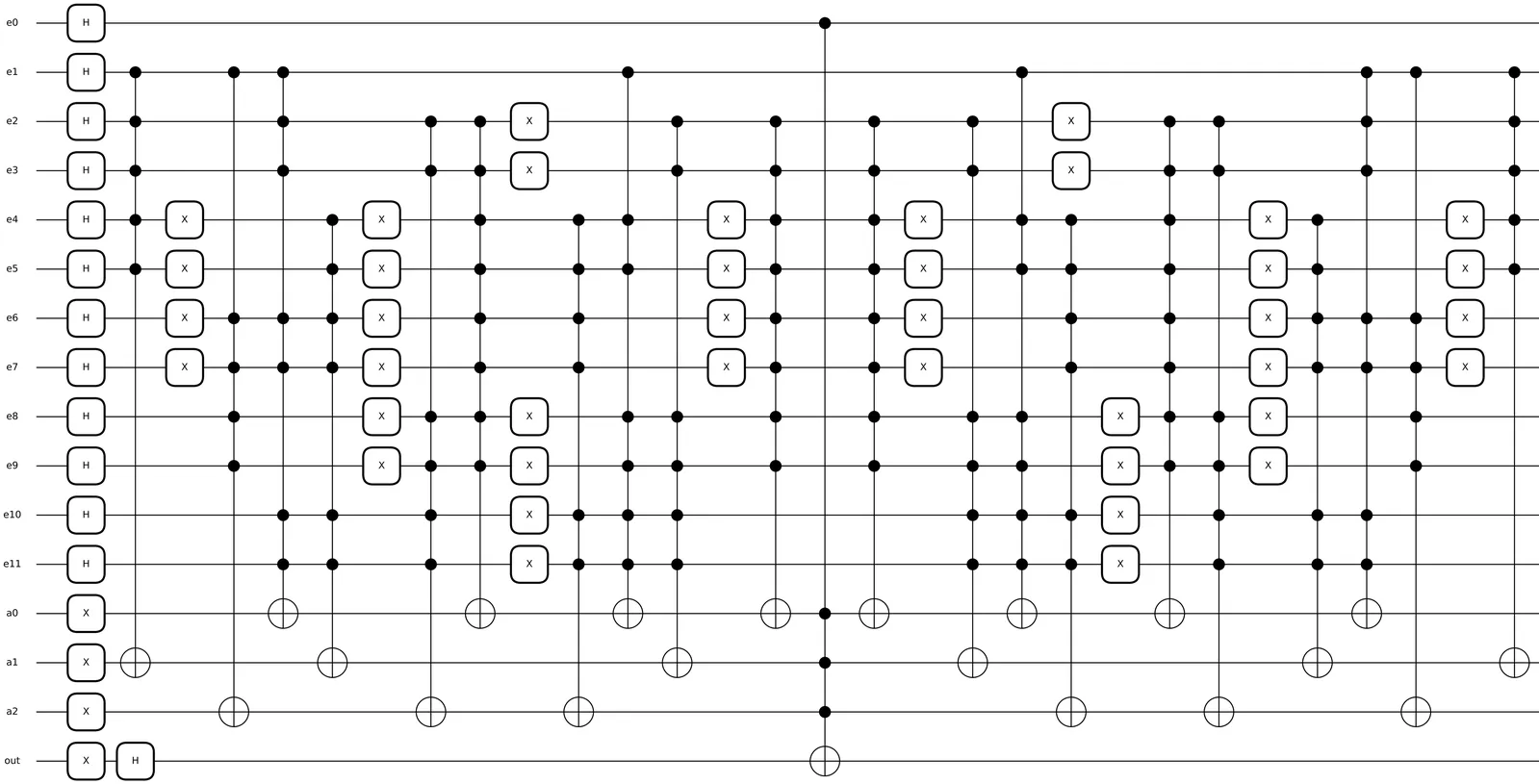
Qubits and Vacuum Amplitudes
High-energy colliders, such as the Large Hadron Collider (LHC) at CERN, are genuine quantum machines, so, in line with Richard Feynman's original motivation for Quantum Computing, the scattering processes that take place there are natural candidates to be simulated on a quantum system. Potential applications range from quantum machine learning methods for collider data analysis, to faster and more precise evaluations of intricate multiloop Feynman diagrams, more efficient jet clustering, improved simulations of parton showers, and many other tasks. In this work, the focus will be on two specific applications: first, the identification of the causal structure of multiloop vacuum amplitudes, a key ingredient of the Loop-Tree Duality and an area with deep connections to graph theory; and second, the integration and sampling of high-dimensional functions. The latter constitutes a first step toward the realization of a fully fledged quantum event generator operating at high perturbative orders.
2601.00722
Jan 2026High Energy Physics - Phenomenology
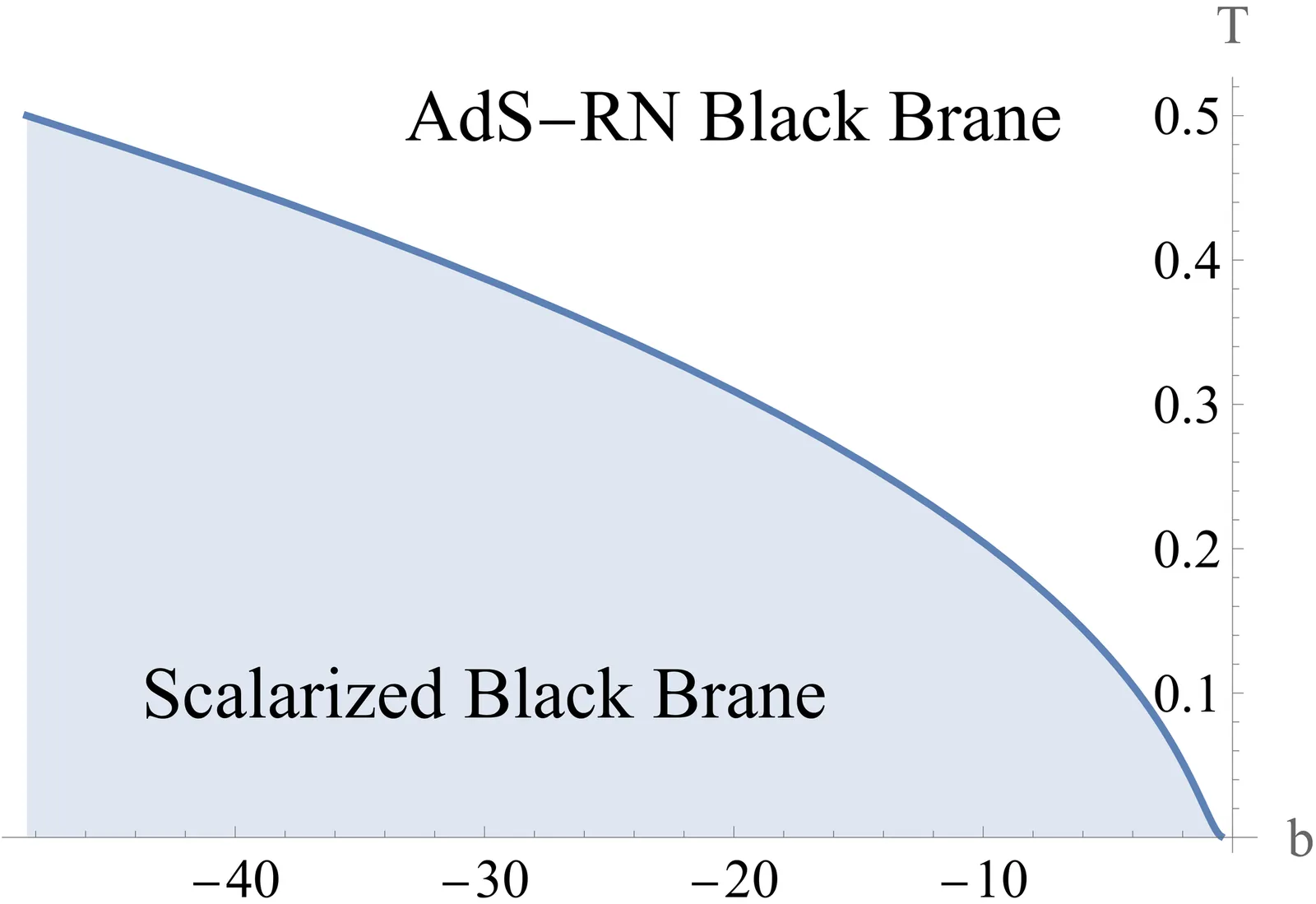
Diagnosing Critical Behavior in AdS Einstein-Maxwell-Scalar Theory via Holographic Entanglement Measures
We investigate the holographic mixed-state entanglement measures in the Einstein-Maxwell-Scalar (EMS) theory. Several quantities are computed, including the holographic entanglement entropy (HEE), mutual information (MI), entanglement wedge cross-section (EWCS), and butterfly velocity ($v_B$). Our findings demonstrate that these measures can effectively diagnose phase transitions. Notably, EWCS and MI, as mixed-state entanglement measures, exhibit behavior opposite to that of the HEE. Additionally, we study the butterfly velocity, a dynamic quantum information measure, and observe that it behaves differently from the static quantum information measures. We propose that the butterfly velocity is initially dominated by entanglement and subsequently by thermal entropy as the coupling constant increases. Moreover, we examine the scaling behavior of the holographic entanglement measures and find that all the critical exponents are equal to $1$, which is twice that of the scalar field. We also explore the inequality between EWCS and MI, noting that the growth rate of MI consistently exceeds that of EWCS during phase transitions. These features are expected to be universal across thermodynamic phase transitions, with the inequalities becoming more significant as one moves away from the critical point.
2601.00069
Dec 2025High Energy Physics - Theory
 2601.00662
2601.00662Extended BMS representations and strings
We construct in detail the irreducible representations of the BMS group with super rotations in three and four dimensions that have the same rest frame momenta as the massive and massless Poincare point particles. We compare these representations to those of the Poincare group and also to the analogous representations of global BMS. We argue that these extended BMS representations are carried by a string rather than a point particle. The super rotations play a crucial role in our discussions.
2601.00662
Jan 2026High Energy Physics - Theory
The JLMS formula in a large code with approximate error correction
Gauge/gravity duality is often described as a quantum error correcting code. However, as seen in the Jafferis-Lewkowycz-Maldacena-Suh (JLMS) formula, exact quantum error correction with complementary recovery (and thus entanglement wedge reconstruction) emerges only in the limit $G \to 0$. As a result, precise arguments controlling error terms have focused on what we call `small' codes which, as $G \to 0$, describe only perturbative excitations near a given classical solution. Such settings are quite restrictive and, in particular, they prohibit discussion of any modular flow that would change the classical background. As a result, they forbid consideration of modular flows generated by semiclassical bulk states at order-one modular parameters. In contrast, we present a single `large' code for the bulk theory that can accommodate such flows and, in particular, in the $G \to 0$ limit includes superpositions of states associated with distinct classical backgrounds. This large code is assembled from small codes that each satisfy an approximate Faulkner-Lewkowycz-Maldacena formula. In this extended setting we clarify the meaning of the (approximate) JLMS relation between bulk and boundary modular Hamiltonians and quantify its validity in an appropriate class of states.
2601.004421
Jan 2026High Energy Physics - Theory
Introduction to black hole thermodynamics
These are the lecture notes for a course at the "Roberto Salmeron School in Mathematical Physics" held at the University of Brasilia in September 2025, to be published in the proceedings book "Modern topics in mathematical physics." The course provides a concise and biased introduction to black hole thermodynamics. It covers the laws of black hole mechanics, Hawking radiation, Euclidean quantum gravity methods, and AdS black holes.
2512.24929
Dec 2025High Energy Physics - Theory

Correlators are simpler than wavefunctions
Several recent works have revealed a simplicity in equal-time correlators that is absent in their wavefunction counterparts. In this letter, we show that this arises from the simple fact that the correlator is obtained by integrating Feynman propagators over the full spacetime, as opposed to the half-space for the wavefunction. Several striking new properties of correlators for any graph are made obvious from this picture. Certain patterns of poles that appear in the wavefunction do not appear in the correlator. The correlator also enjoys several remarkable factorization properties in various limits. Most strikingly, the correlator admits a systematic Laurent expansion in the neighborhood of every pole, with the first subleading term vanishing for every pole. There is an especially simple understanding of the expansion around the total energy pole up to second order, given by a differential operator acting on the amplitude. Finally, we show how these results extend beyond single graphs to the full correlator in Tr $φ^3$ theory.
2512.237951
Dec 2025High Energy Physics - Theory

Sommerfeld Enhancement from Background Force and the Galactic Center GeV Excess
We study the impact of background-induced forces on dark matter (DM) annihilation and their implications for indirect detection. In the presence of a finite number density of background particles, loop-level interactions can generate an effective force that is significantly enhanced relative to the vacuum case. We construct a two-component DM model in which the dominant component is a fermionic particle $χ$ and the subdominant component is an ultralight pseudoscalar particle $φ$. The annihilation of $χ$ proceeds through the p-wave channel and produces gamma-ray emission. The finite density of $φ$ particles induces a background-enhanced force between $χ$ particles, leading to a sizable Sommerfeld enhancement of the annihilation. We show that a viable region of parameter space in this model can account for the gamma-ray excess observed in the Galactic Center using Fermi-LAT data. The background-induced force substantially amplifies the Sommerfeld enhancement and thus enlarges the parameter space capable of explaining the excess, highlighting the importance of background effects in astrophysical environments.
2512.24188
Dec 2025High Energy Physics - Phenomenology
Energy correlators in four-dimensional gravity
We investigate energy correlators in four-dimensional gravitational theories, which provide a simple class of infrared-finite observables. We compute the one- and two-point energy correlators at one loop in $\mathcal{N}=8$ supergravity and in pure Einstein gravity, with particular emphasis on the contact terms arising from the interplay between virtual corrections and real emissions. We explicitly demonstrate the cancellation of infrared divergences and verify the Ward identities associated with energy-momentum conservation. In the back-to-back limit, we derive an all-order expression for the energy-energy correlator, showing that it is governed by universal soft-graviton dynamics. We further introduce a particularly simple beam-averaged energy-energy correlator and compute it in different gravitational theories, including tree-level string theory. The resulting correlators exhibit analyticity and polynomial boundedness, allowing for the formulation of dispersion relations, which we explore. Finally, we discuss additional singularities of the gravitational energy correlators, absent in QCD, that originate from the long-range nature of the gravitational interactions.
2512.23791
Dec 2025High Energy Physics - Theory

Quantum dynamics of perfect fluids
We study the quantum field theory of zero temperature perfect fluids. Such systems are defined by quantizing a classical field theory of scalar fields $φ^I$ that act as Lagrange coordinates on an internal spatial manifold of fluid configurations. Invariance under volume preserving diffeomorphisms acting on these scalars implies that the long-wavelength spectrum contains vortex (transverse modes) with exact $ω_T=0$ dispersion relation. As a result, physically interpreting the perturbative quantization of this theory by standard methods has proven to be challenging. In this paper, we show that correlators evaluated in the class of semi-classical (Gaussian) initial states prepared at $t=0$ are well-defined and accessible via perturbation theory. The width of the initial state effectively acts as an infrared regulator without explicitly breaking diffeomorphism invariance. As an application, we compute stress tensor two-point correlators and show that vortex modes give a non-trivial contribution to the response function, non-local in both space and time.
2512.23793
Dec 2025High Energy Physics - Theory
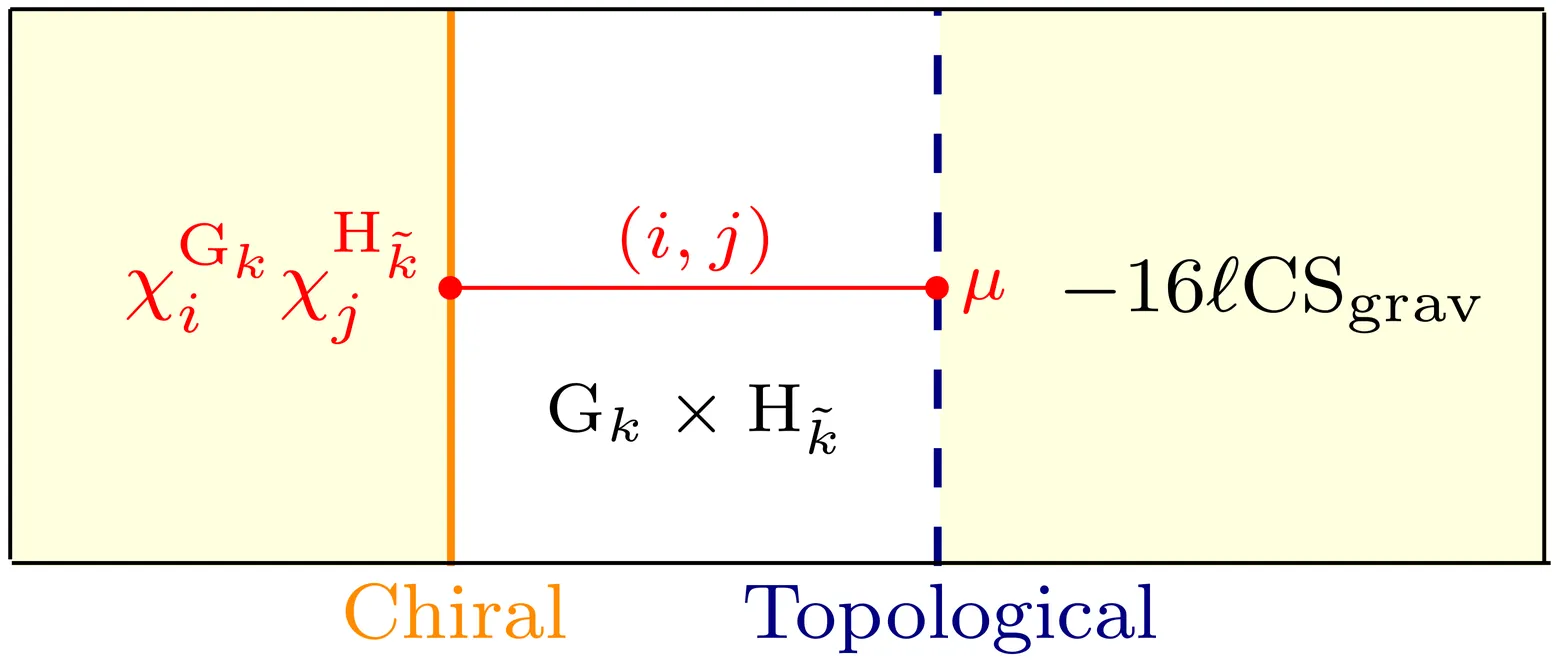
Generalized Level-Rank Duality, Holomorphic Conformal Field Theory, and Non-Invertible Anyon Condensation
We study the interplay between holomorphic conformal field theory and dualities of 3D topological quantum field theories generalizing the paradigm of level-rank duality. A holomorphic conformal field theory with a Kac-Moody subalgebra implies a topological interface between Chern-Simons gauge theories. Upon condensing a suitable set of anyons, such an interface yields a duality between topological field theories. We illustrate this idea using the $c=24$ holomorphic theories classified by Schellekens, which leads to a list of novel sporadic dualities. Some of these dualities necessarily involve condensation of anyons with non-abelian statistics, i.e. gauging non-invertible one-form global symmetries. Several of the examples we discover generalize from $c=24$ to an infinite series. This includes the fact that Spin$(n^{2})_{2}$ is dual to a twisted dihedral group gauge theory. Finally, if $-1$ is a quadratic residue modulo $k$, we deduce the existence of a sequence of holomorphic CFTs at central charge $c=2(k-1)$ with fusion category symmetry given by $\mathrm{Spin}(k)_{2}$ or equivalently, the $\mathbb{Z}_{2}$-equivariantization of a Tambara-Yamagami fusion category.
2512.24419
Dec 2025High Energy Physics - Theory
 2512.25005
2512.25005Grassmannian Geometries for Non-Planar On-Shell Diagrams
On-shell diagrams are gauge invariant quantities which play an important role in the description of scattering amplitudes. Based on the principles of generalized unitarity, they are given by products of elementary three-point amplitudes where the kinematics of internal on-shell legs are determined by cut conditions. In the ${\cal N}=4$ Super Yang-Mills (SYM) theory, the dual formulation for on-shell diagrams produces the same quantities as canonical forms on the Grassmannian $G(k,n)$. Most of the work in this direction has been devoted to the planar diagrams, which dominate in the large $N$ limit of gauge theories. On the mathematical side, planar on-shell diagrams correspond to cells of the positive Grassmannian $G_+(k,n)$ which have been very extensively studied in the literature in the past 20 years. In this paper, we focus on the non-planar on-shell diagrams which are relevant at finite $N$. In particular, we use the triplet formulation of Maximal-Helicity-Violating (MHV) on-shell diagrams to obtain certain regions in the Grassmannian $G(2,n)$. These regions are unions of positive Grassmannians with different orderings (referred to as oriented regions). We explore the features of these unions, and show that they are pseudo-positive geometries, in contrast to positive geometry of a single oriented region. For all non-planar diagrams which are \emph{internally planar} there always exists a strongly connected geometry, and for those that are \emph{irreducible}, there exists a geometry with no spurious facets. We also prove that the already known identity moves, square and sphere moves, form the complete set of identity moves for all MHV on-shell diagrams.
2512.25005
Dec 2025High Energy Physics - Theory
 2512.19370
2512.19370From $\mathrm{d} \! \log$ to $\mathrm{d} \mathcal{E}$: Canonical Elliptic Integrands and Modular Symbol Letters with Pure eMPLs
We propose '$\mathrm{d} \mathcal{E}$-forms' as fundamental building blocks of canonical integrands for elliptic Feynman integrals, which lead to Kronecker-Eisenstein $ω$-form symbol letters. Built upon pure elliptic multiple polylogarithms, they provide a natural extension of the '$\mathrm{d} \! \log$-form' integrands and $\mathrm{d} \! \log$ letters for polylogarithmic cases. By introducing an extended basis treating all marked points equally, we manifest a hidden symmetry structure in the canonical connection matrix, and demonstrate its covariance under modular transformations. Our result provides a novel perspective on describing canonical bases and symbol letters in a unified language of pure functions.
2512.19370
Dec 2025High Energy Physics - Theory
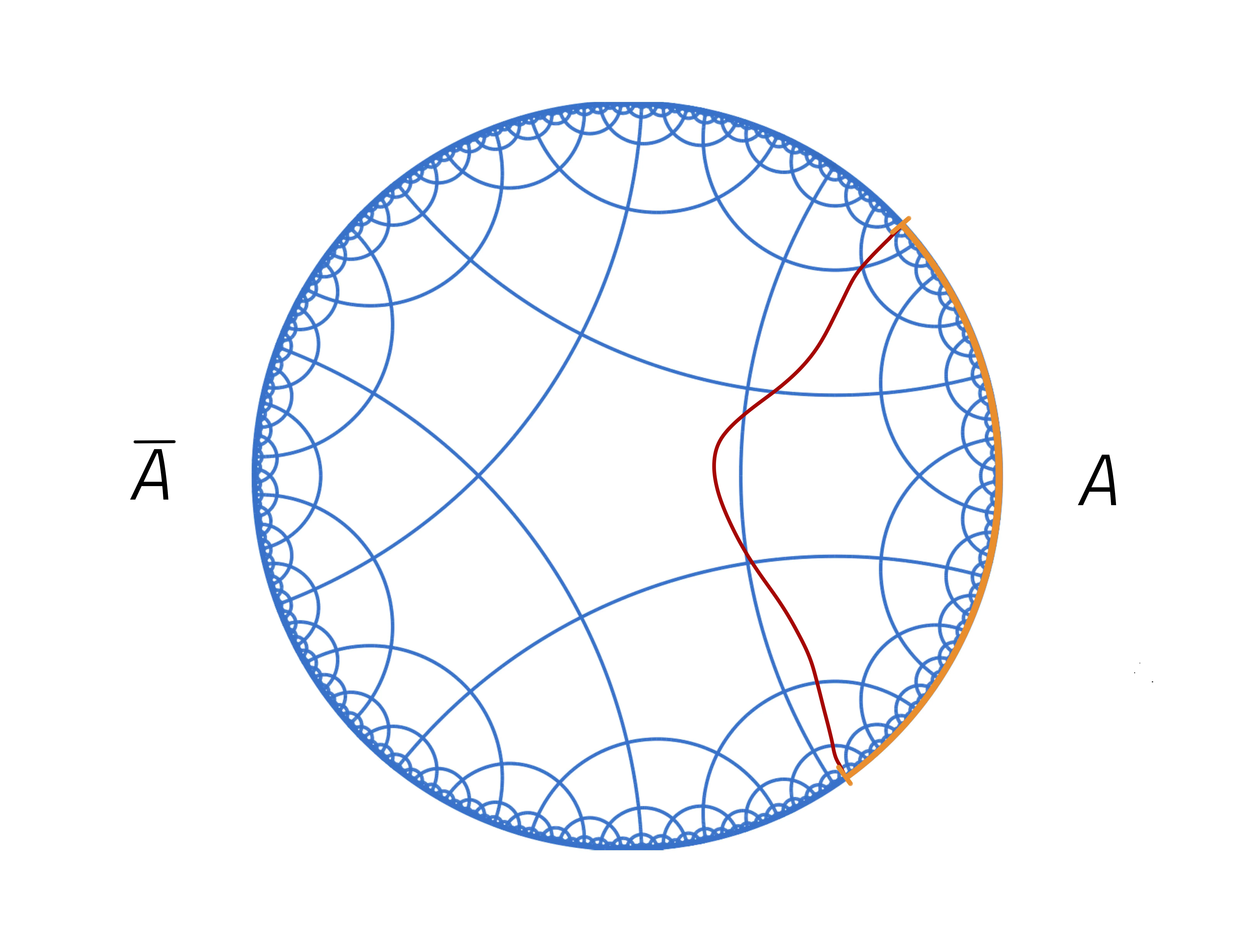
Holographic Tensor Networks as Tessellations of Geometry
Holographic tensor networks serve as toy models for the Anti-de Sitter/Conformal Field Theory (AdS/CFT) correspondence, capturing many of its essential features in a concrete manner. However, existing holographic tensor network models remain far from a complete theory of quantum gravity. A key obstacle is their discrete structure, which only approximates the semi-classical geometry of gravity in a qualitative sense. In \cite{Lin:2024dho}, it was shown that a network of partial-entanglement-entropy (PEE) threads, which are bulk geodesics with a specific density distribution, generates a perfect tessellation of AdS space. Moreover, such PEE-network tessellations can be constructed for more general geometries using the Crofton formula. In this paper, we assign a quantum state to each vertex in the PEE network and develop two holographic tensor network models: the factorized PEE tensor network, which takes the form of a tensor product of EPR pairs, and the random PEE tensor network. In both models we reproduce the exact Ryu-Takayanagi formula by showing that the minimal number of cuts along a homologous surface in the network exactly computes the area of this surface.
2512.19452
Dec 2025High Energy Physics - Theory
Higher lattice gauge theory from representations of 2-groups and 3+1D topological phases
We construct a higher lattice gauge theory based on the representation of 2-groups described by a category of crossed modules on a lattice model described by path 2-groupoids. Using these lattice gauge representations, an exactly solvable Hamiltonian for topological phases in 3+1 dimensions is constructed. We show that the ground states of this model are topological observables.
2512.19608
Dec 2025High Energy Physics - Lattice
Exotic Branes and Symmetries of String Theory
Are duality transformations symmetries of string theory? For AdS space-time the answer is no for generic asymptotic values of the moduli, since the duality symmetry is broken explicitly in the dual conformal field theory. In contrast, in string theory in flat space-time, monodromy around codimension two exotic branes show that duality transformations are spontaneously broken discrete gauge symmetries with observable consequences, provided macroscopic loops of these branes are not hidden behind an event horizon. We discuss how this can be achieved and how the situation in flat space-time differs from that in AdS space-time. We also discuss observability of codimension two non-BPS branes and codimension one BPS and non-BPS branes.
2512.19068
Dec 2025High Energy Physics - Theory
 2512.19498
2512.19498Six-loop gravitational interactions at the sixth post-Newtonian order
We compute the gravitational interaction of two coalescing compact objects at sixth post-Newtonian order in the static limit, employing the diagrammatic approach within the effective field theory framework of General Relativity. The calculation requires the evaluation of six-loop Feynman diagrams that are mapped onto two-point integrals with a gauge-theory-like structure, which are computed here for the first time. The resulting seventh-order contribution in Newton's constant is finite in three space dimensions. This result provides the most technically demanding missing ingredient for the determination of the conservative dynamics of the gravitational two-body system at sixth post-Newtonian order.
2512.19498
Dec 2025High Energy Physics - Theory