High Energy Physics - Lattice

arXiv:hep-lat

Lattice field theory methods and applications, including algorithms and numerical techniques.

Looking for a broader view? This category is part of:

Trending in High Energy Physics - Lattice

Higher lattice gauge theory from representations of 2-groups and 3+1D topological phases

We construct a higher lattice gauge theory based on the representation of 2-groups described by a category of crossed modules on a lattice model described by path 2-groupoids. Using these lattice gauge representations, an exactly solvable Hamiltonian for topological phases in 3+1 dimensions is constructed. We show that the ground states of this model are topological observables.

2512.19608

Dec 2025High Energy Physics - Lattice

Related categories:

High Energy Physics - Experiment High Energy Physics - Phenomenology High Energy Physics - Theory

735 papers

QCD Crossover at Low Temperatures from Lee-Yang Edge Singularity

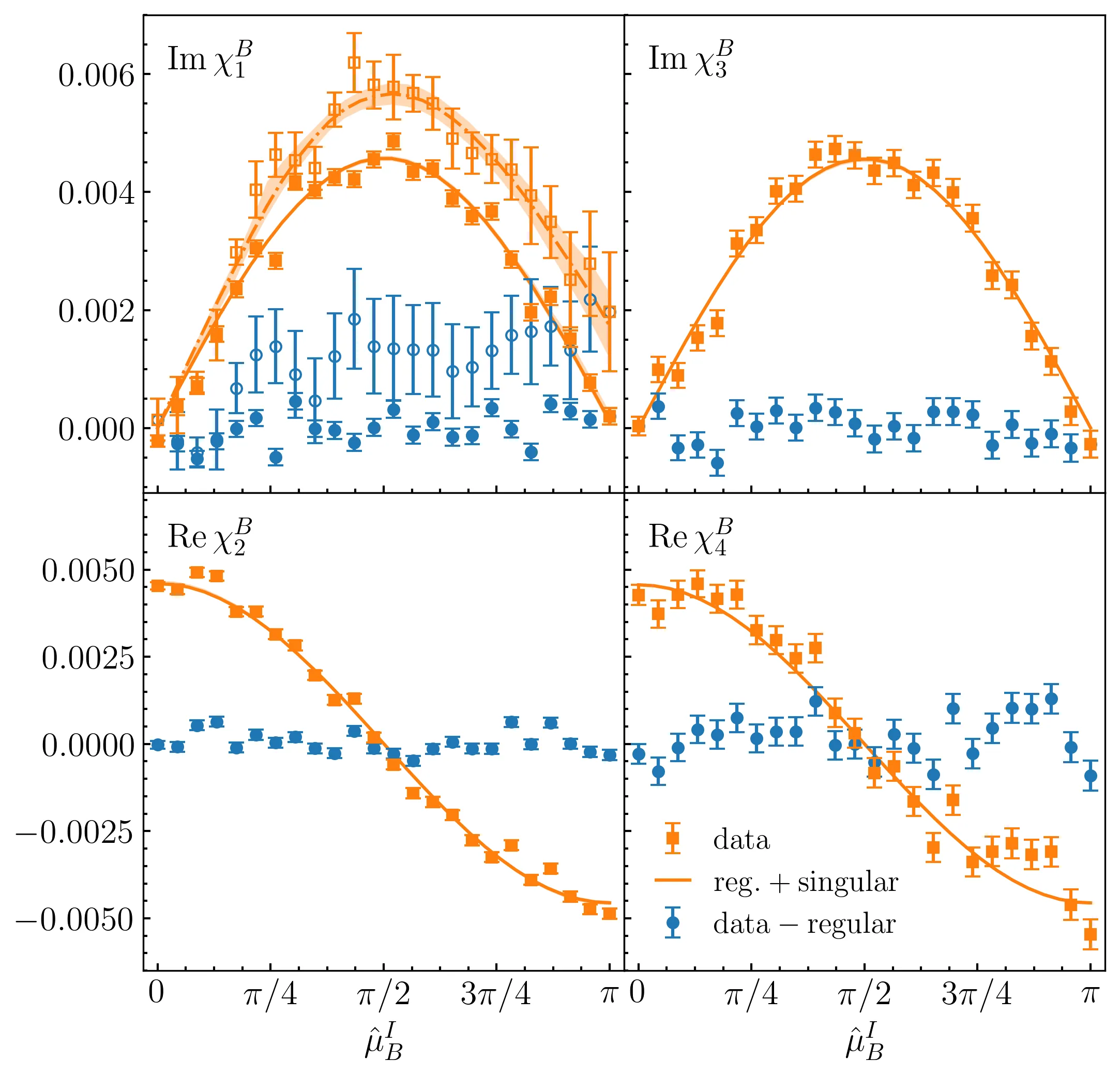
We provide the first lattice-QCD estimate of the crossover line down to $T\simeq108$~MeV. We introduce a new method that combines the Lee-Yang edge in the complex plane of baryon chemical potential $μ_B$ with universal chiral scaling to determine the $μ_B$ dependence of the QCD chiral critical and pseudo-critical temperatures. By performing $(2\!+\!1)$-flavor lattice QCD simulations at $T\simeq108$~MeV and purely imaginary $μ_B$ with a single lattice spacing and two volumes, we compute $μ_B$-dependent baryon-number susceptibilities and extract the location of the Lee-Yang edge. Together with universal scaling near the QCD chiral transition, it constrains the mapping function between $\{T,μ_B\}$ and the scaling variable (\textit{i.e.}\ the argument of the universal scaling functions). This mapping function then yields the $μ_B$ dependence of the critical and pseudo-critical temperatures for $T\gtrsim108$~MeV. While our calculation is performed only at a single value of low temperature without explicit input from small-$μ_B$ expansion, the resulting $μ_B$ dependence of the pseudo-critical temperature is consistent with established lattice-QCD determinations at small $μ_B$ and compatible with chemical freeze-out parameters of heavy-ion collisions down to low temperatures, demonstrating the validity and robustness of the method. Application of this method can be systematically extended to additional temperatures and finer discretizations, opening a pathway to charting the QCD phase diagram in the low-$T$, high-$μ_B$ regime.

2601.04782Jan 2026

View

Three-particle scattering amplitudes from lattice QCD

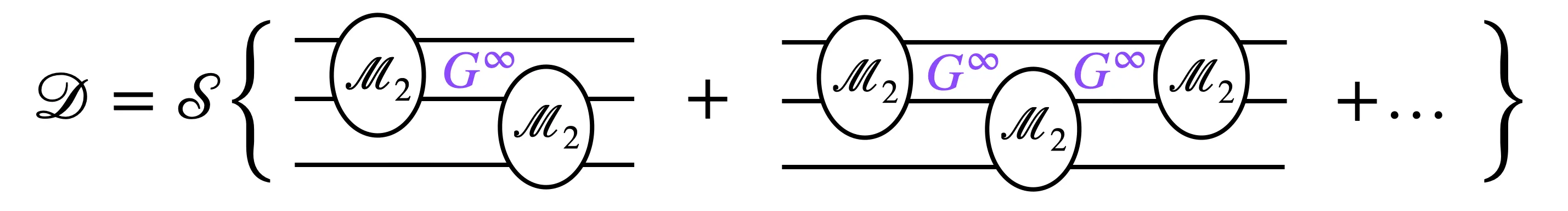
I review recent progress in calculating scattering amplitudes and resonance properties involving three particles using results from lattice QCD. The necessary input is the finite-volume spectrum, and the outputs -- via solutions of integral equations -- are scattering amplitudes that can be continued into the complex plane to search for resonance poles. I describe the outlook for future extensions and applications of this work.

2601.04147Jan 2026

View

Phases of the $q$-deformed $\mathrm{SU}(N)$ Yang-Mills theory at large $N$

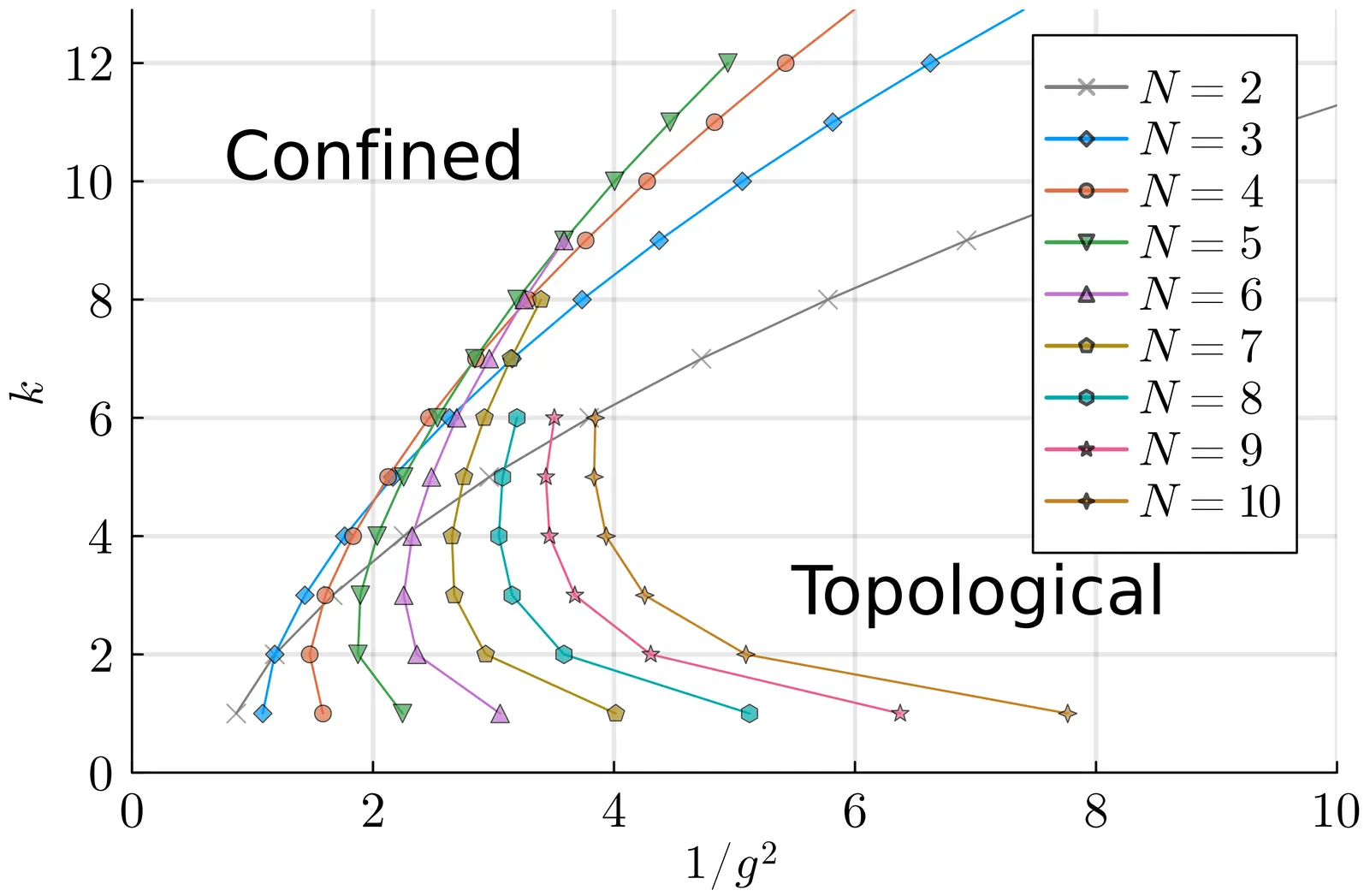
We investigate the $(2+1)$-dimensional $q$-deformed $\mathrm{SU}(N)_k$ Yang-Mills theory in the lattice Hamiltonian formalism, which is characterized by three parameters: the number of colors $N$, the coupling constant $g$, and the level $k$. By treating these as tunable parameters, we explore how key properties of the theory, such as confinement and topological order, emerge in different regimes. Employing a variational mean-field analysis that interpolates between the strong- and weak-coupling regimes, we determine the large-$N$ phase structure in terms of the 't Hooft coupling $λ_\mathrm{tH}=g^2N$ and the ratio $k/N$. We find that the topologically ordered phase remains robust at large $N$ under appropriate scalings of these parameters. This result indicates that the continuum limit of large-$N$ gauge theory may be more intricate than naively expected, and motivates studies beyond the mean-field theory, both to achieve a further understanding of confinement in gauge theories and to guide quantum simulations of large-$N$ gauge theories.

2601.03843Jan 2026

View

Tensor renormalization group approach to critical phenomena via symmetry-twisted partition functions

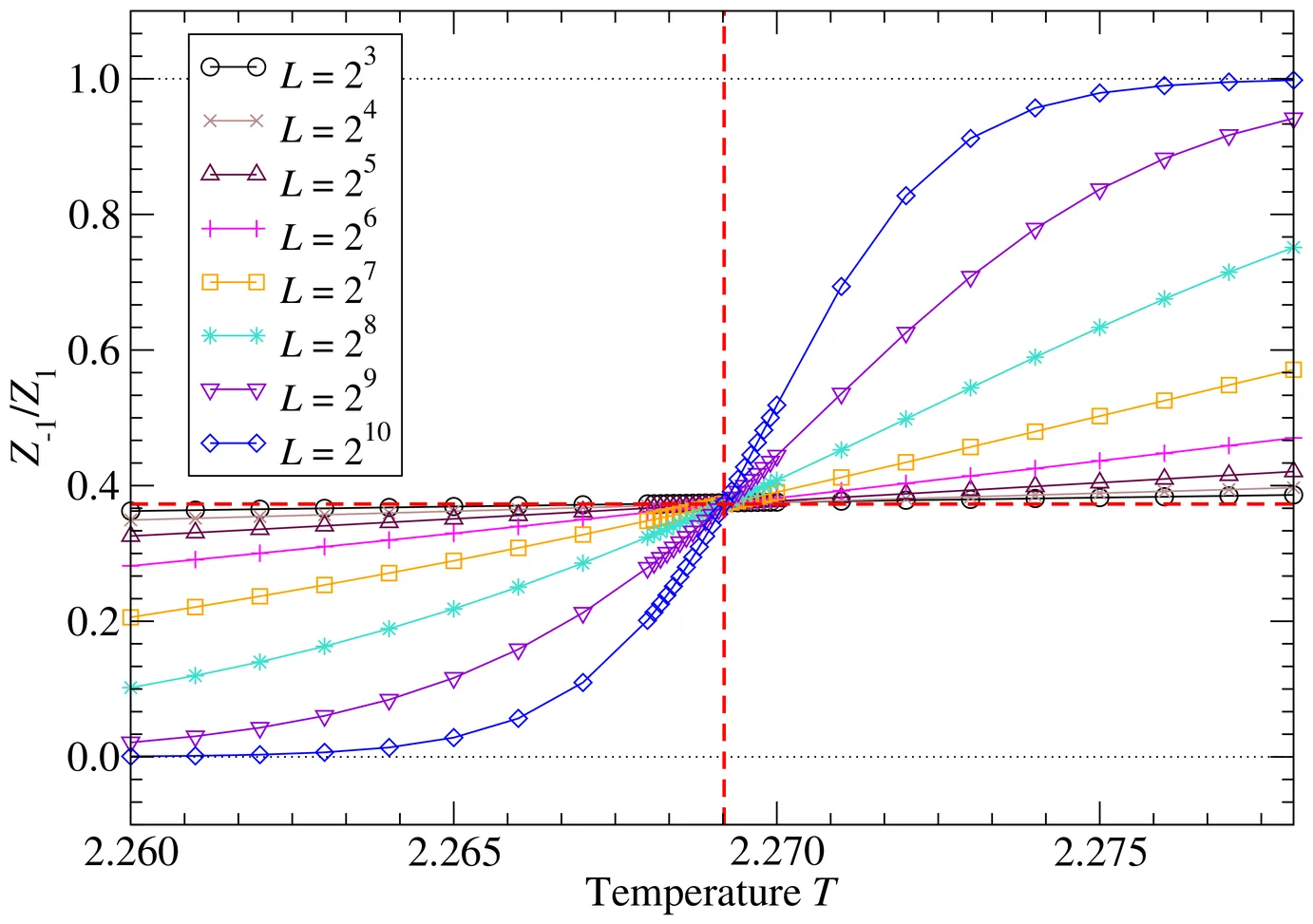
The locality of field theories strongly constrains the possible behaviors of symmetry-twisted partition functions, and thus they serve as order parameters to detect low-energy realizations of global symmetries, such as spontaneous symmetry breaking (SSB). We demonstrate that the tensor renormalization group (TRG) offers an efficient framework to compute the symmetry-twisted partition functions, which enables us to detect the symmetry-breaking transition and also to study associated critical phenomena. As concrete examples of SSB, we investigate the two-dimensional (2D) classical Ising model and the three-dimensional (3D) classical $O(2)$ nonlinear sigma model, and we identify their critical points solely from the twisted partition function. By employing the finite-size scaling argument, we find the critical temperature $T_c=2.2017(2)$ with the critical exponent $ν= 0.663(33)$ for the 3D $O(2)$ model. In addition, we also study the Berezinskii-Kosterlitz-Thouless (BKT) criticality of the 2D classical $O(2)$ model by extracting the helicity modulus from the twisted partition functions, and we obtain the BKT transition temperature, $T_{\mathrm{BKT}}=0.8928(2)$.

2601.02681Jan 2026

View

The Nucleon Axial Form Factor from Averaging Lattice QCD Results

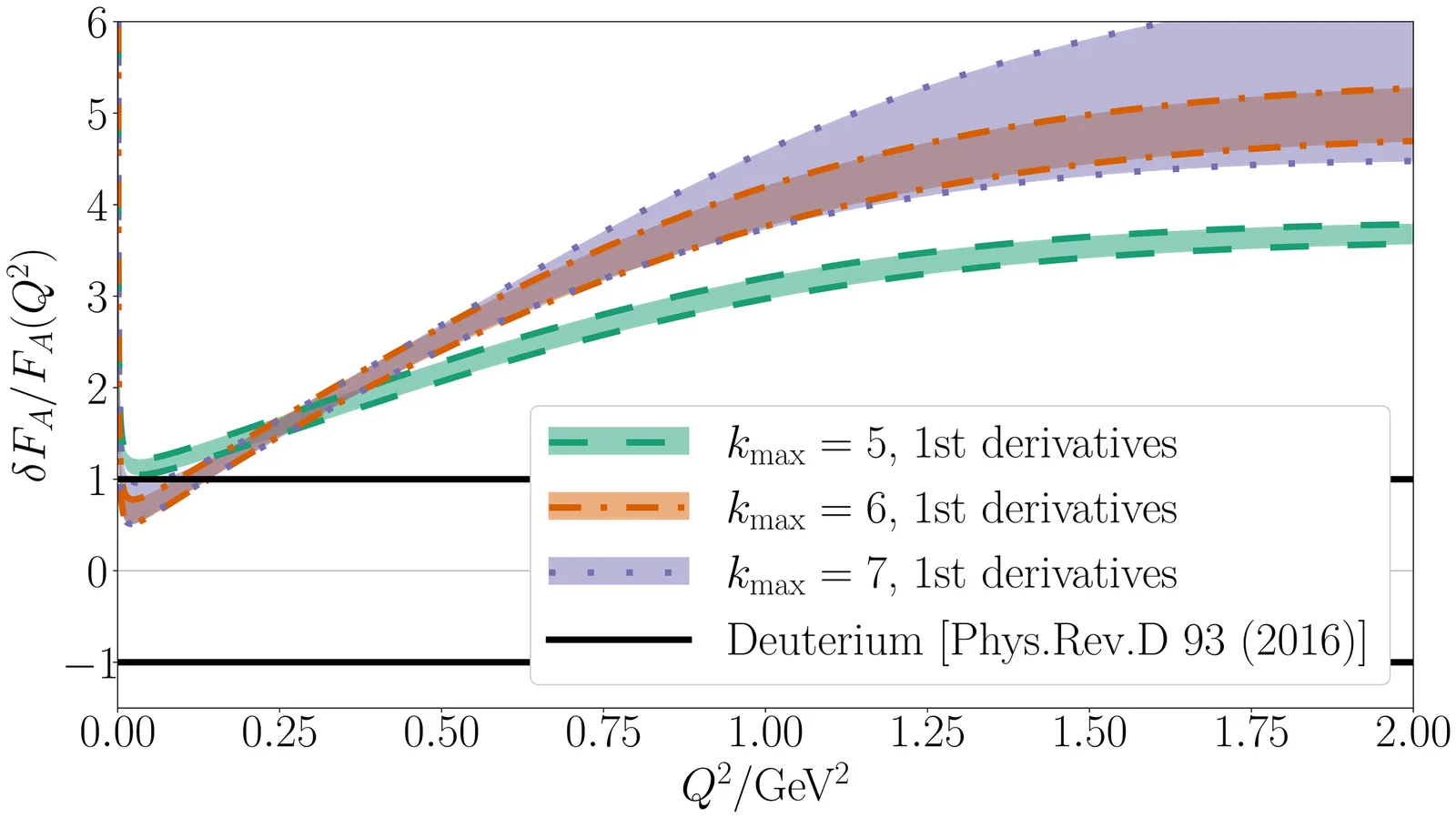
Flagship neutrino oscillation experiments depend on precise and accurate theoretical knowledge of neutrino-nucleon cross sections across a variety of energies and interaction mechanisms. Key ingredients to the amplitudes that make up these cross sections are parameterized form factors. The axial form factor describing a weak interaction with a nucleon is part of one of the primary neutrino-nucleon interaction mechanisms, quasielastic scattering, yet this form factor is uncertain and its precision is limited by the availability of data for a neutrino scattering with nucleons or small nuclear targets. Lattice Quantum Chromodynamics (LQCD) now offers another approach for obtaining mathematically rigorous constraints of the axial form factor from theoretical calculations with complete systematic error budgets. In this work, strategies for averaging LQCD results are explored, including both a random sampling of form factor values across momentum transfers as well as an averaging strategy based on analytic calculations of form factor derivatives. Fits to z expansion parameterizations are reported and compared against neutrino-hydrogen and neutrino-deuterium scattering data.

2601.02676Jan 2026

View

Symmetric mass generation as a multicritical point with enhanced symmetry

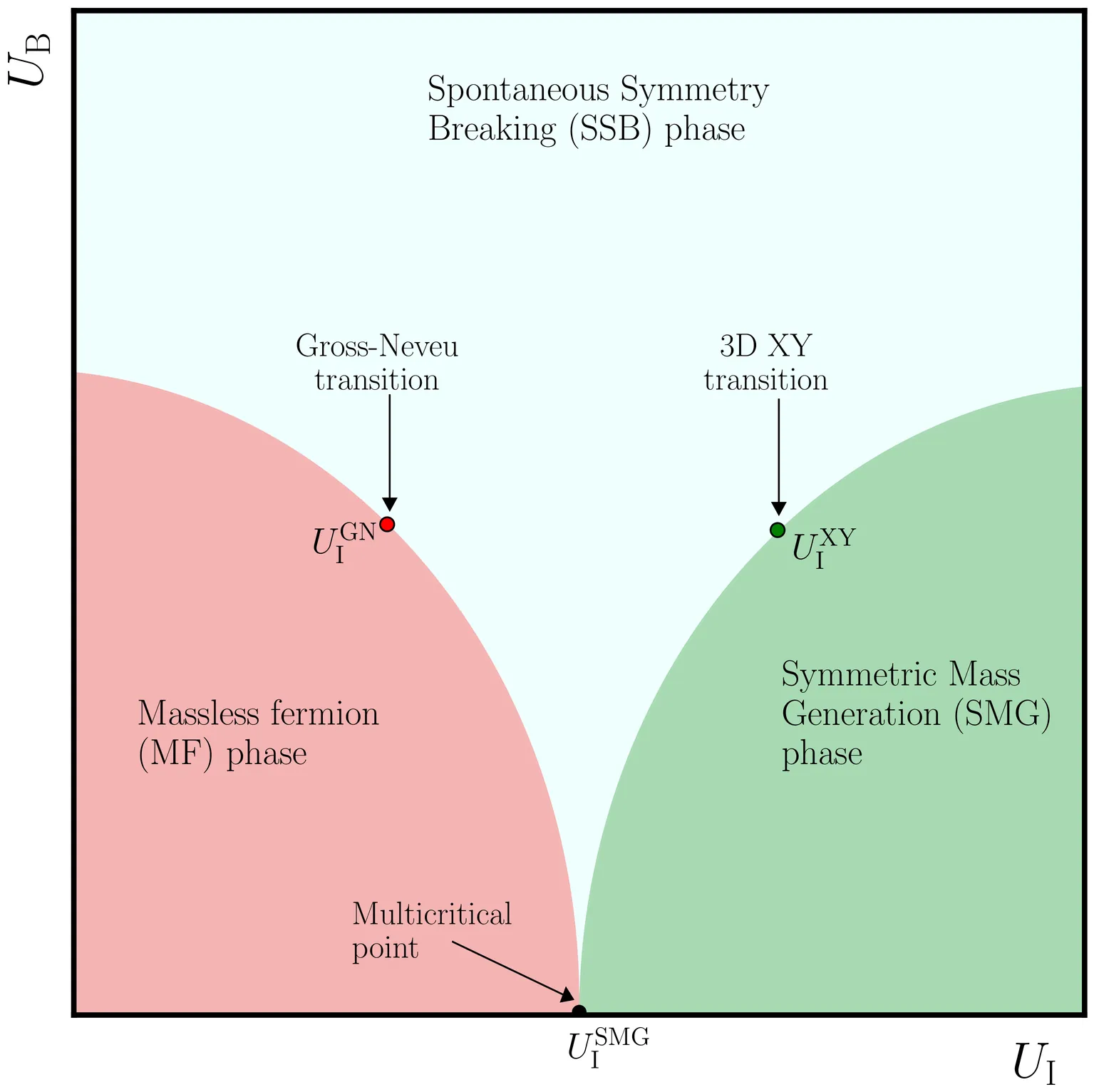
We explore the phase diagram of a lattice fermion model that exhibits three distinct phases: a massless fermion (MF) phase; a massive fermion phase with spontaneous symmetry breaking (SSB) induced by a fermion bilinear condensate; and a massive fermion phase with symmetric mass generation (SMG). Using the fermion-bag Monte Carlo method on large cubical lattices, we find evidence for traditional second-order critical points separating the first two and the latter two phases. Remarkably, these critical points appear to merge at a multicritical point with enhanced symmetry when the symmetry breaking parameter is tuned to zero, giving rise to the recently discovered direct second-order transition between the massless and symmetric massive fermion phases.

2512.24836Dec 2025

View

Total Gluon Helicity Contribution to Proton Spin from Lattice QCD

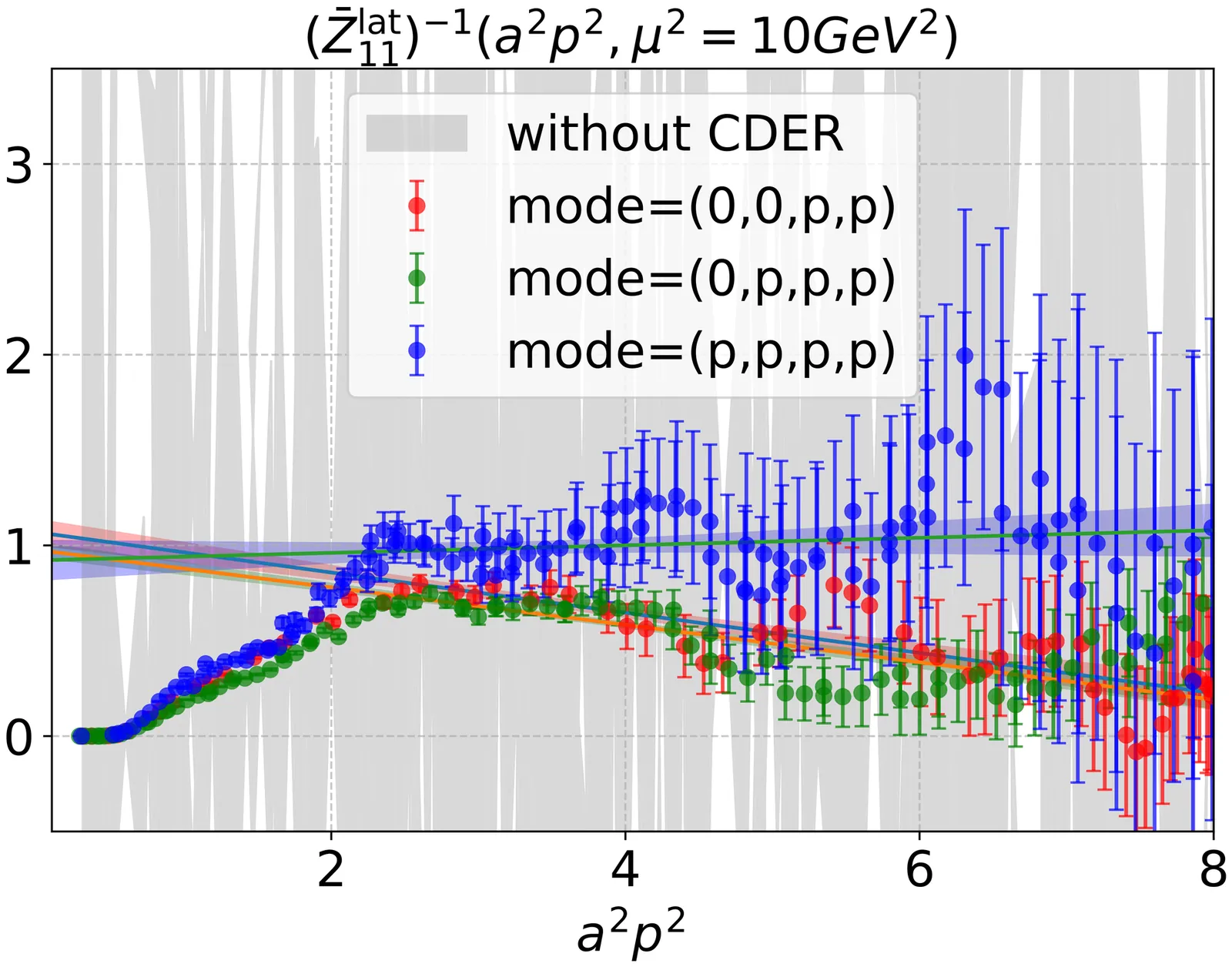
We report a state-of-the-art lattice QCD calculation of the total gluon helicity contribution to proton spin, $ΔG$. The calculation is done on ensembles at three different lattice spacings $a=\{0.08, 0.09, 0.11\}$ fm. By employing distillation + momentum smearing for proton external states, we extract the bare matrix elements of the topological current $K^μ$ under the 5-HYP smeared Coulomb gauge fixing configurations. Furthermore, we apply a non-perturbative $\mathrm{RI/MOM}$ renormalization scheme augmented with the Cluster Decomposition Error Reduction (CDER) technique to determine the renormalization constants of $K^μ$. The results obtained from different components $K^{t,i}$ (with $i$ being the direction of proton momentum or polarization) are consistent with Lorentz covariance within uncertainties. After extrapolating to the continuum limit, $ΔG$ is found to be $ΔG = 0.231(17)^{\mathrm{sta.}}(33)^{\mathrm{sym.}}$ at the $\overline{\mathrm{MS}}$ scale $μ^2=10\ \mathrm{GeV}^2$, which constitutes approximately $46(7)\%$ of the proton spin.

2512.24315Dec 2025

View

Spectral reconstruction based on dimensional reduction in high-temperature gauge theories

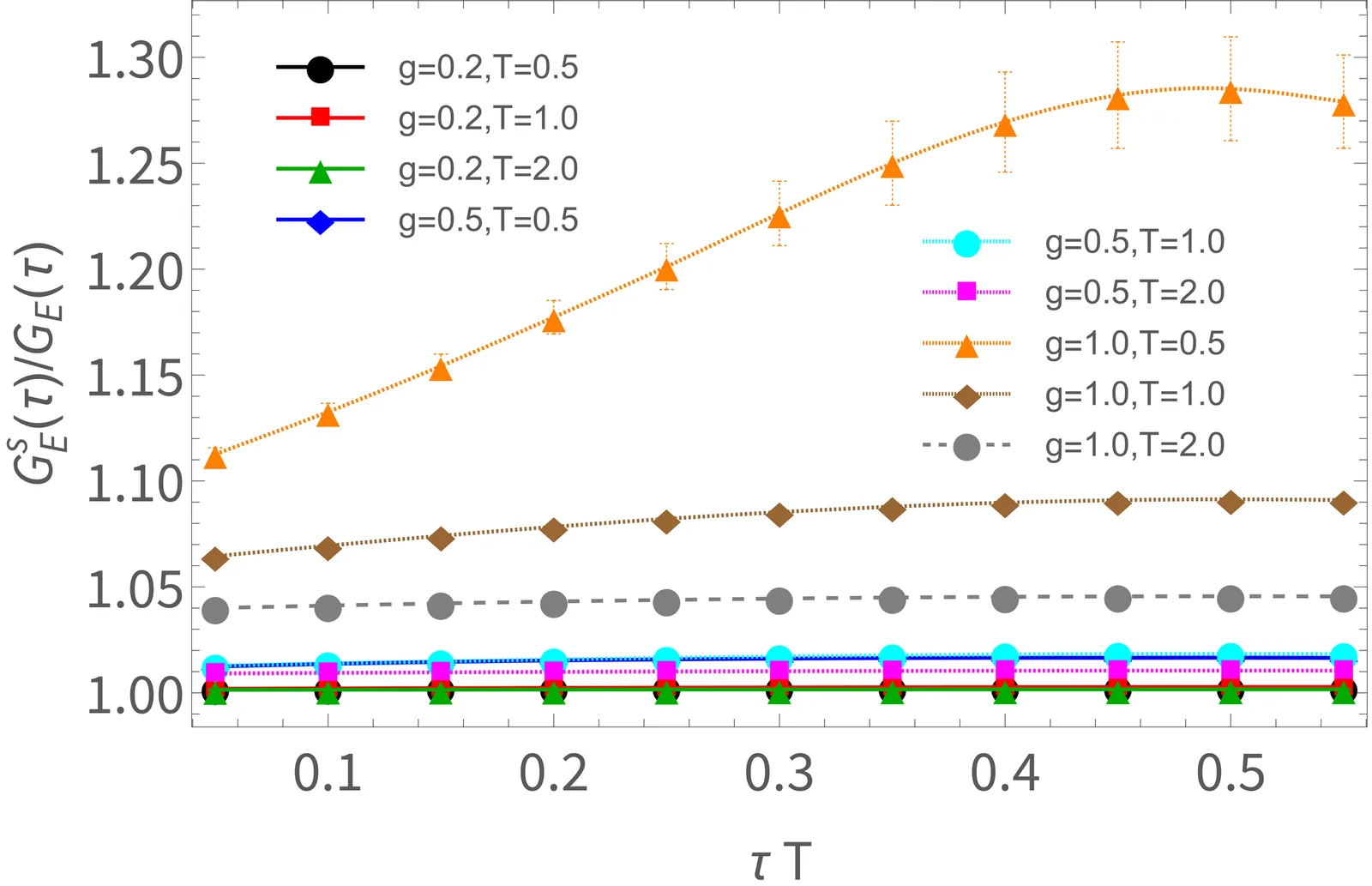
We propose a numerical spectral reconstruction workflow for high-temperature gauge theories that incorporates elements of semi-classical real-time evolution directly into standard lattice QCD simulations via high-temperature dimensional reduction, thus counteracting the deterioration of Euclidean-time correlators at high temperatures. With a moderate numerical cost, our method allows to estimate spectral functions with parametrically better frequency resolution as compared with spectral reconstruction methods based on Euclidean-time correlators alone. The method is tested on a simple (1+1)-dimensional Abelian gauge theory with fermions, where our method precisely reproduces the full quantum spectral functions calculated using exact numerical diagonalization in the high-temperature, weak-coupling regime. We also demonstrate the feasibility of our approach by applying it to light-quark meson correlators in lattice QCD deep in the deconfinement regime.

2512.23560Dec 2025

View

2512.22609

Minimal-doubling and single-Weyl Hamiltonians

We develop a systematic Hamiltonian formulation of minimally doubled lattice fermions in (3+1) dimensions, derive their nodal structures (structures of zeros), and classify their symmetry patterns for both four-component Dirac and two-component Weyl constructions. Motivated by recent single-Weyl proposals based on Bogoliubov-de Gennes (BdG) representation, we argue that the corresponding single-Weyl Hamiltonians are obtained from the minimal-doubling Hamiltonians supplemented by an appropriate species-splitting mass term, and we re-examine the non-onsite symmetry protecting the physical Weyl node in terms of a Ginsparg-Wilson-type relation. We then construct a one-parameter family of deformations that preserves all the symmetries and demonstrate that, once the parameter exceeds a critical value, additional Weyl nodes emerge and the system exits the single-node regime. This indicates that in interacting theories radiative corrections can generate symmetry-allowed counterterms, so maintaining the desired single-Weyl phase generically requires "moderate" parameter tuning.

2512.22609Dec 2025

View

Rotationally invariant dynamical lattice regulators for Euclidean quantum field theories

We introduce a dynamical-lattice regulator (DLR) for Euclidean quantum field theories on a fixed hypercubic graph $Λ\simeq \mathbb{Z}^d$, in which the embedding $x:Λ\to \mathbb{R}^d$ is promoted to a dynamical field and integrated over subject to shape-regularity constraints. The total action is local on $Λ$, gauge invariant, and depends on $x$ only through Euclidean invariants built from edge vectors (local metrics, volumes, etc.), hence the partition function is exactly covariant under the global Euclidean group SE(d) at any lattice spacing. The intended symmetry-restoring mechanism is not rigid global zero modes but short-range *local twisting* of the embedding that mixes local orientations; accordingly, our universality discussion is conditioned on a short-range geometry hypothesis (SR): after quotienting the global SE(d) modes, connected correlators of local geometric observables have correlation length O(1) in lattice units. We prove Osterwalder-Schrader reflection positivity for the coupled system with embedding $x$ and generic gauge/matter fields $(U,Φ)$ in finite volume by treating $x$ as an additional multiplet of scalar fields on $Λ$. Assuming (SR), integrating out $x$ at fixed cutoff yields a local Symanzik effective action in which geometry fluctuations generate only SO(d)-invariant irrelevant operators and finite renormalizations; in particular, in $d=4$ we recover the standard one-loop $β$-function in a scalar $φ^4$ test theory. Finally, we describe a practical local Monte Carlo update and report $d=2$ proof-of-concept simulations showing a well-behaved geometry sector and a substantial reduction of axis-vs-diagonal cutoff artifacts relative to a fixed lattice at matched bare parameters.

2512.22072Dec 2025

View

Quantum Ising Model on $(2+1)-$Dimensional Anti$-$de Sitter Space using Tensor Networks

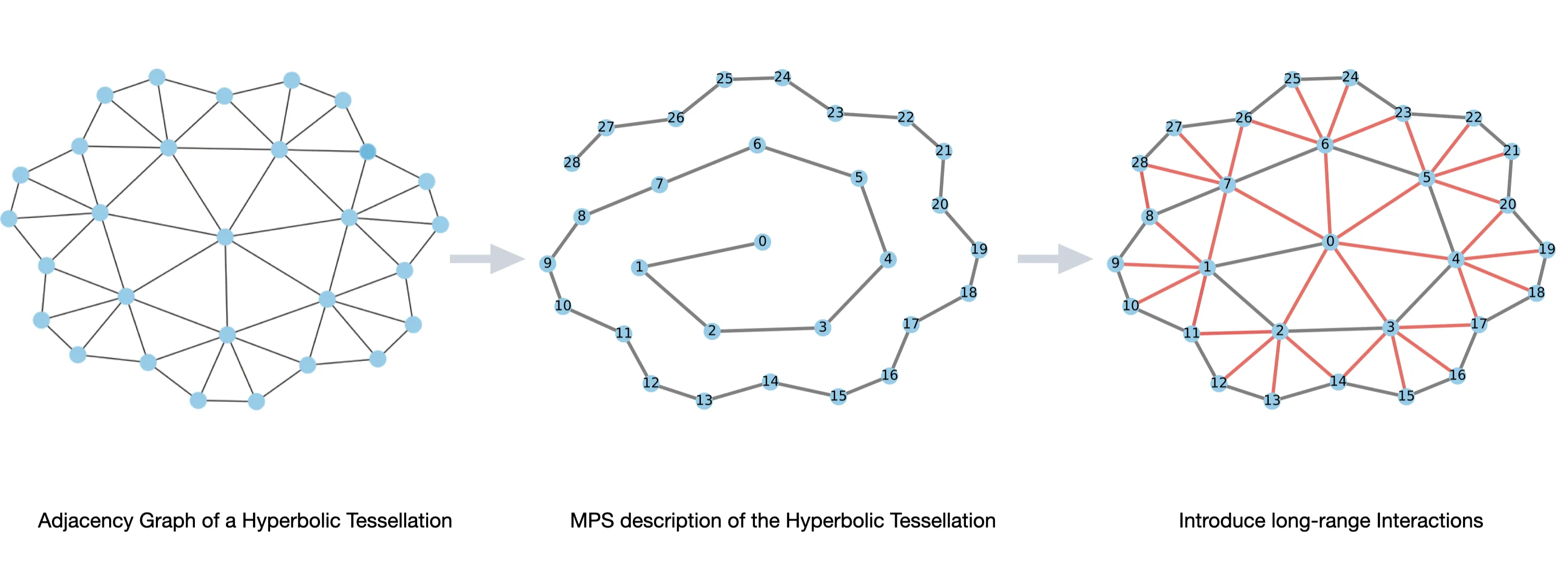
We study the quantum Ising model on (2+1)-dimensional anti-de Sitter space using Matrix Product States (MPS) and Matrix Product Operators (MPOs). Our spatial lattices correspond to regular tessellations of hyperbolic space with coordination number seven. We find the ground state of this model using the Density Matrix Renormalization Group (DMRG) algorithm which allowed us to probe lattices that range in size up to 232 sites. We explore the bulk phase diagram of the theory and find disordered and ordered phases separated by a phase transition. We find that the boundary-boundary spin correlation function exhibits power law scaling deep in the disordered phase of the Ising model consistent with the anti-de Sitter background. By tracing out the bulk indices, we are able to compute the density matrix for the boundary theory. At the critical point, we find the entanglement entropy exhibits the logarithmic dependence of boundary length expected for a one-dimensional CFT but away from this, we see a linear scaling. In comparison, the full system exhibits a volume law scaling, which is expected in chaotic and highly connected systems. We also measure Out-of-time-Ordered-Correlators (OTOCs) to explore the scrambling behavior of the theory.

2512.208381Dec 2025

View

Efficient Learning of Lattice Gauge Theories with Fermions

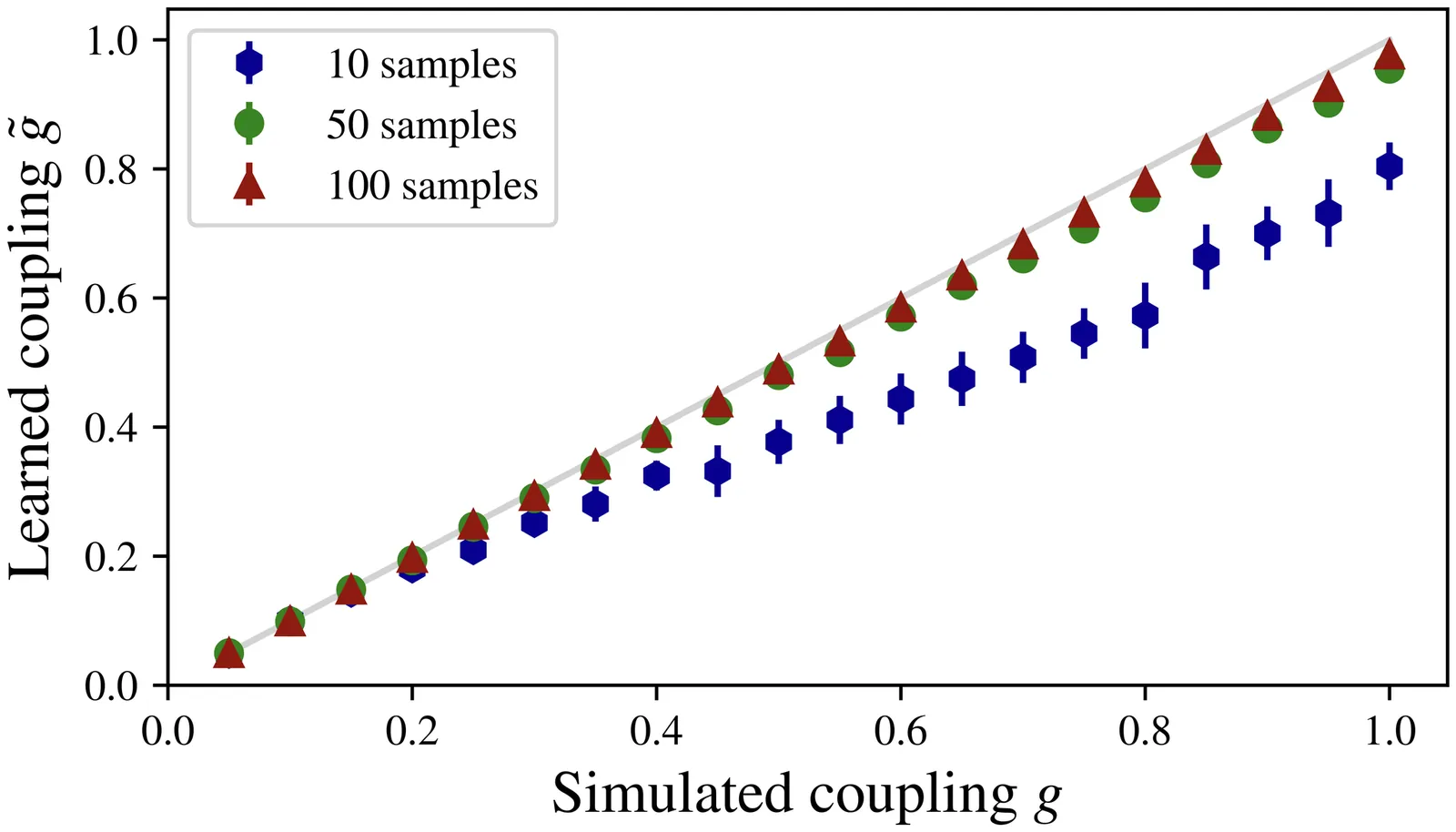
We introduce a learning method for recovering action parameters in lattice field theories. Our method is based on the minimization of a convex loss function constructed using the Schwinger-Dyson relations. We show that score matching, a popular learning method, is a special case of our construction of an infinite family of valid loss functions. Importantly, our general Schwinger-Dyson-based construction applies to gauge theories and models with Grassmann-valued fields used to represent dynamical fermions. In particular, we extend our method to realistic lattice field theories including quantum chromodynamics.

2512.19891Dec 2025

View

Higher lattice gauge theory from representations of 2-groups and 3+1D topological phases

2512.19608Dec 2025

View

The fermion sign problem in Gauss law sectors of quantum link models with dynamical matter

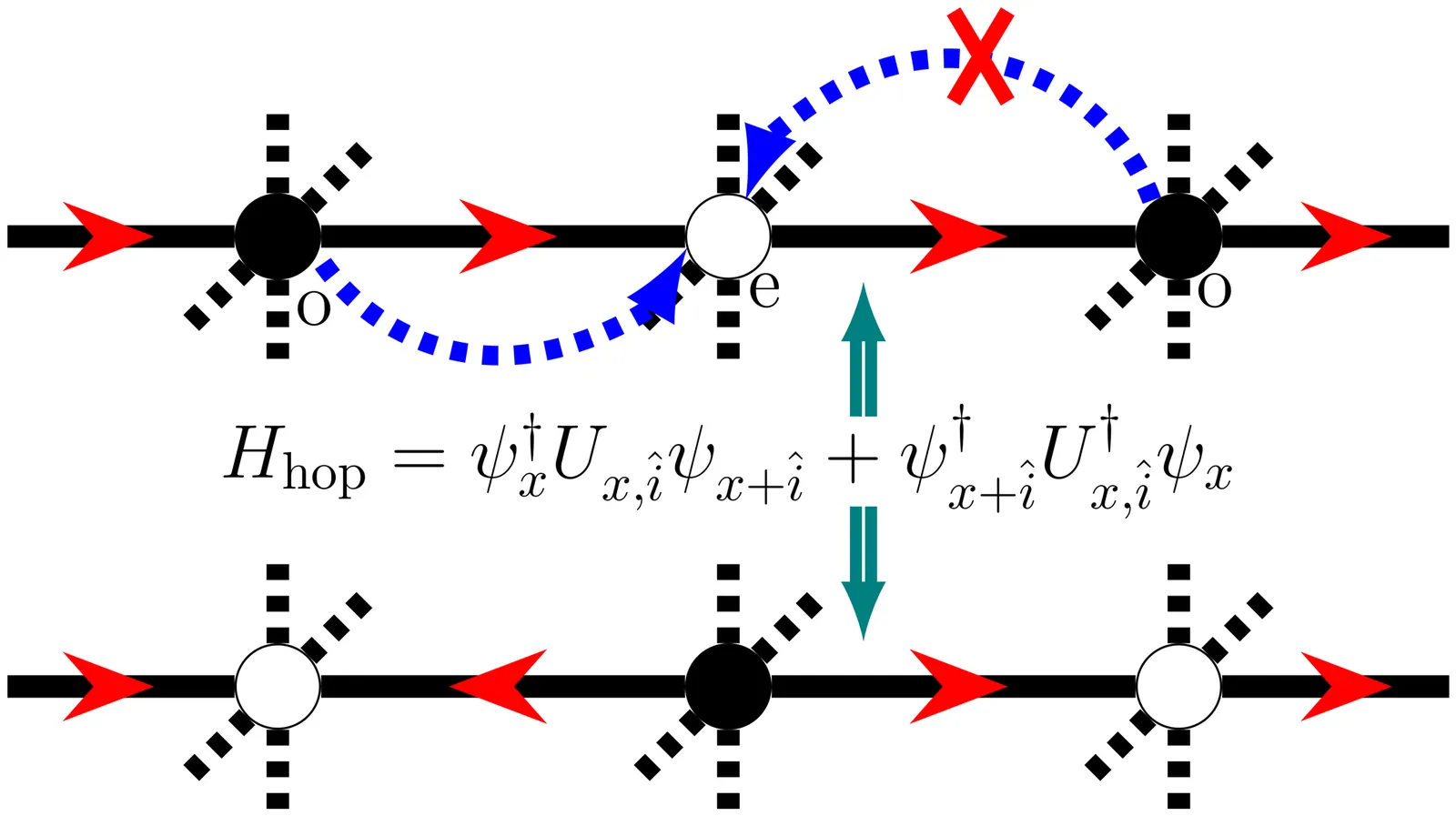
The fermion sign problem poses a formidable challenge to the use of Monte Carlo methods for lattice gauge theories with dynamical fermionic matter fields. A meron cluster algorithm recently formulated for gauge fields represented as spin-$\frac{1}{2}$ quantum links coupled to a single flavour of staggered fermions samples only two of the exponentially many Gauss law (GL) sectors at low temperatures, making it possible to simulate either of those two GL sectors at zero temperature in polynomial time. In this article, we analytically identify GL sectors which can be simulated without encountering the fermion sign problem in arbitrary spatial dimensions. Using large-scale exact diagonalization and cluster Monte Carlo methods, we further explore the nature of phases in the GL sectors dominating at zero temperature. The vacuum states lie in sectors which satisfy a staggered Gauss law, in contrast to the zero GL sector familiar in particle physics. Moreover, we prove that while the ground state GL sectors do not suffer from the fermion sign problem, the usual zero-charge GL sector (often considered the physical sector) does. We outline the role of the magnetic energy in causing transitions between GL sectors. We expect our results to be valid for truncated Kogut-Susskind gauge theories, beyond quantum link models.

2512.14833Dec 2025

View

Complex Langevin simulations with a kernel

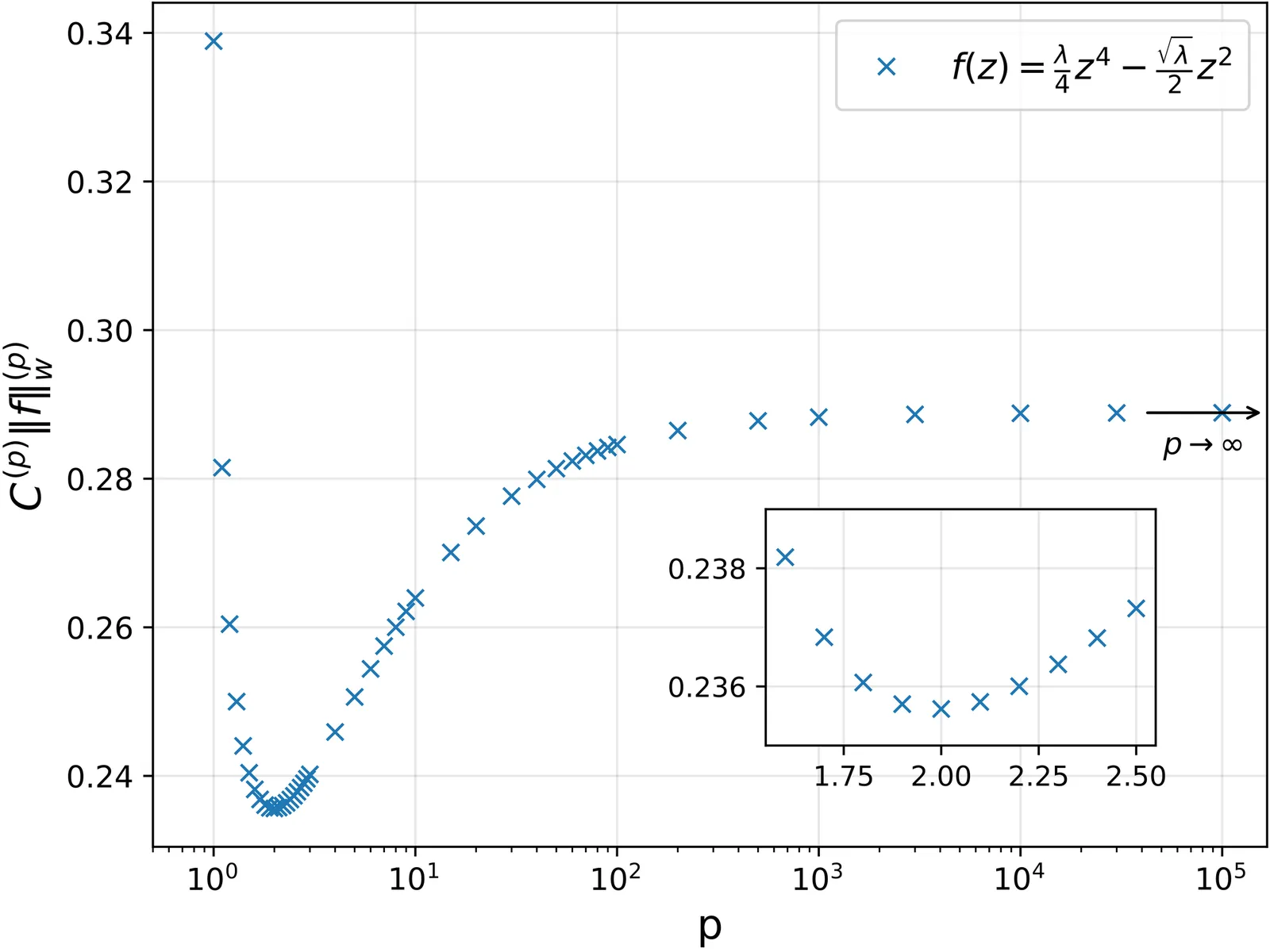
We discuss recent developments regarding the use of kernels in complex Langevin simulations. In particular, we outline how a kernel can be used to solve the problem of wrong convergence in a simple toy model. Since conventional correctness criteria for complex Langevin results are only necessary but not sufficient, the correct convergence of complex Langevin simulations is not always straightforward to assess. Hence, we furthermore discuss a condition for correctness that we have recently derived, which is both necessary and sufficient. Finally, we outline a machine-learning approach for finding suitable kernels in lattice gauge theories and present preliminary results of its application to the heavy-dense limit of QCD.

2512.14153Dec 2025

View

Algorithmic aspects of gauged Gaussian fermionic projected entangled pair states

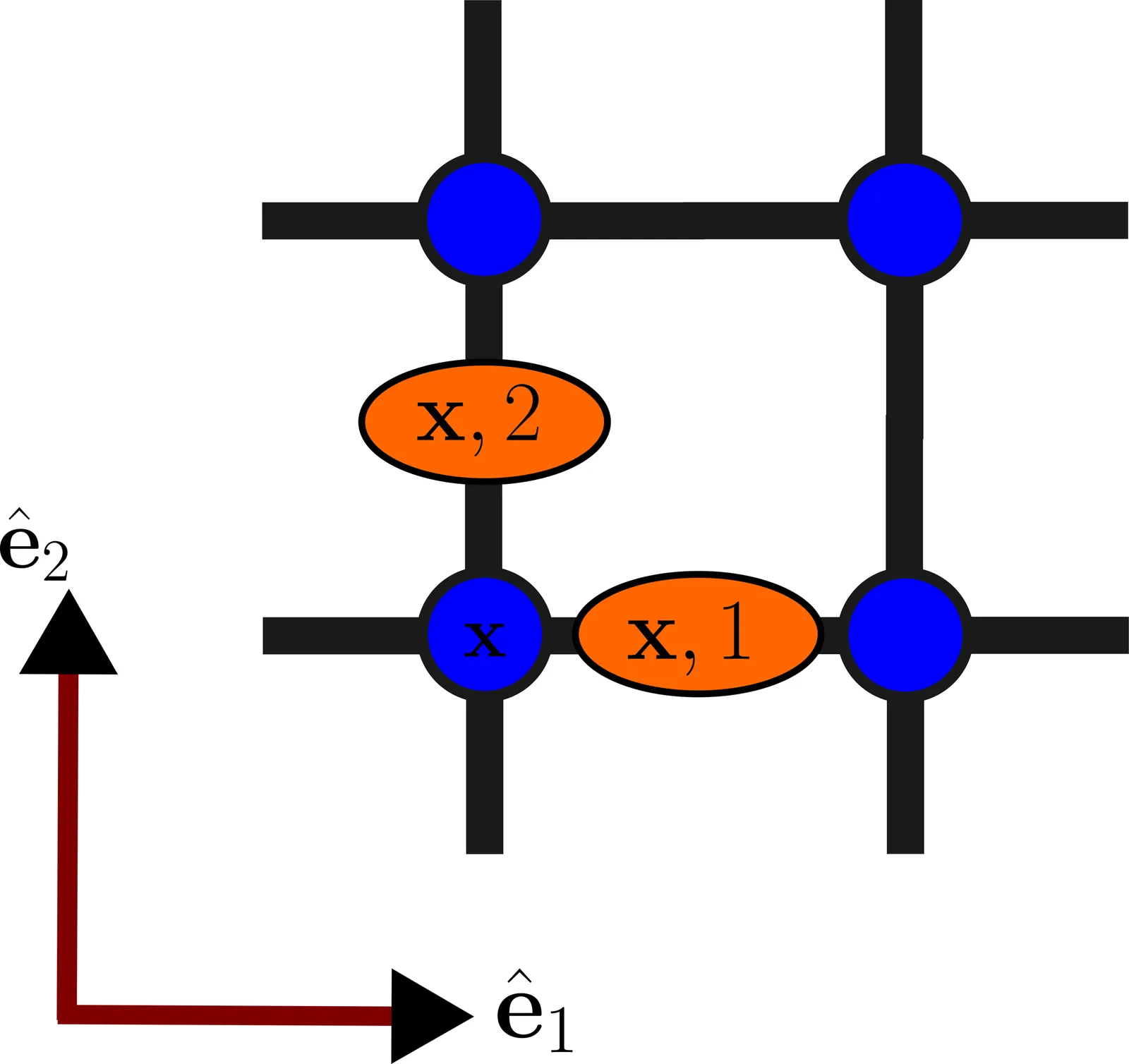
Lattice gauge theories (LGTs) provide a powerful framework for studying non-perturbative phenomena in gauge theories. However, conventional approaches such as Monte Carlo (MC) simulations in imaginary time are limited, as they do not allow real time evolution and suffer from a sign problem in many important cases. Using Gauged Gaussian fermionic projected entangled pair states (GGFPEPS) as a variational ground state ansatz offers an alternative for studying LGTs through a sign-problem-free variational MC. As this method is extended to larger and more complex systems, understanding its numerical behavior becomes essential. While conventional action based MC has been extensively studied, the performance and characteristics of non-action-based MC within the GGFPEPS framework are far less explored. In this work, we investigate these algorithmic aspects, identifying an optimal update size for GGFPEPS-based MC simulations for $\mathbb{Z}_2$ in $2+1$ dimensions. We show that gauge fixing generally slows convergence, and demonstrate that not exploiting the translation-invariance can, in some cases, improve the computational time scaling of error convergence. We expect that these improvements will allow advancing the simulation to larger and more complex systems.

2512.13812Dec 2025

View

The Arf-Brown-Kervaire invariant on a lattice

We propose a lattice formulation of the Arf-Brown-Kervaire (ABK) invariant which takes values in $\mathbb{Z}_8$. Compared to the standard $\mathbb{Z}$-valued index, the ABK invariant is more involved in that it arises in Majorana fermion partition functions with reflection symmetry on two-dimensional non-orientable manifolds, and its definition contains an infinite sum over Dirac eigenvalues that requires proper regularization. We employ the massive Wilson Dirac operator, with and without domain-walls, on standard two-dimensional square lattices, and use its Pfaffian for the definition. Twisted boundary conditions and cross-caps, which reverse the orientation, are introduced to realize nontrivial topologies equipped with nontrivial $\mathrm{Pin}^{-}$ structures of Majorana fermions. We verify numerically (and partly analytically) that our formulation on a torus, Klein bottle, real projective plane (as well as its triple connected sum), and two types of Möbius strip reproduces the known values in continuum theory.

2512.11424Dec 2025

View

Asymptotic-freedom and massive glueballs in a qubit-regularized SU(2) gauge theory

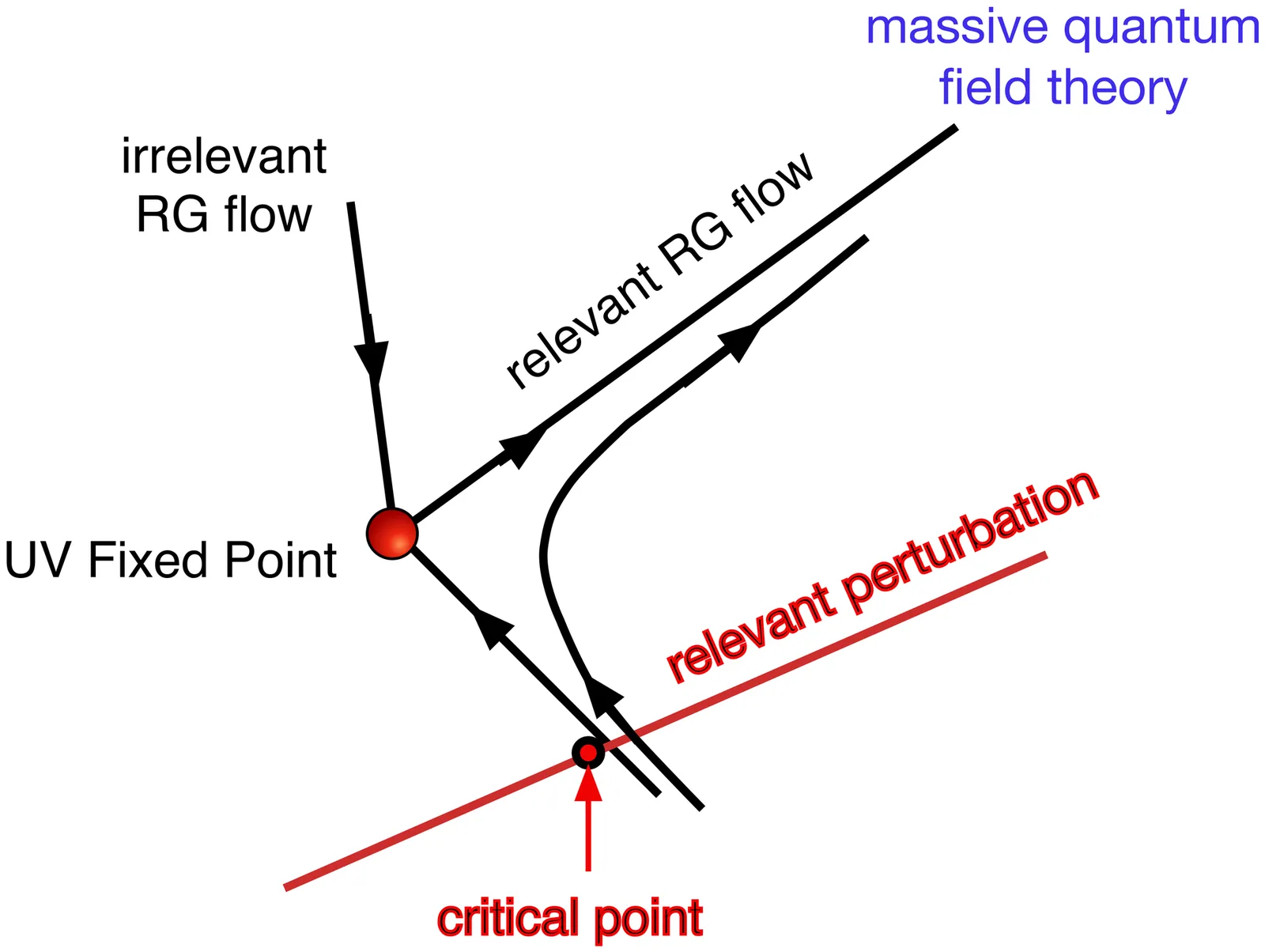
We argue that a simple qubit-regularized $\mathrm{SU}(2)$ lattice gauge theory on a plaquette chain serves as a pseudo-one-dimensional toy model for Yang-Mills theory in three spatial dimensions. We map the chain Hamiltonian to the Transverse Field Ising Model in a uniform magnetic field and demonstrate that it can be tuned to a continuum limit in which the short-distance physics is governed by the asymptotically free Ising conformal field theory describing free Majorana fermions, while the long-distance regime contains massive excitations of the $E_8$ quantum field theory that can be interpreted as one-dimensional analogues of glueballs. Furthermore, we find $\sqrtσ/m_1 = 0.1763(5)$ where $σ$ is the string tension between two static quarks and $m_1$ is the mass of the lightest glueball.

2512.11068Dec 2025

View

2511.13551

SO(3) real algebra method for SU(3) QCD at finite baryon-number densities

For SU(3) lattice QCD calculations at finite baryon-number densities, we propose the ``SO(3) real algebra method'', in which the SU(3) gauge variable is divided into the SO(3) and SU(3)/SO(3) parts. In this method, we introduce the ``maximal SO(3) gauge'' by minimizing the SU(3)/SO(3) part of the SU(3) gauge variable. In the Monte Carlo calculation, the SO(3) real algebra method employs the SO(3) fermionic determinant, i.e., the fermionic determinant of the SO(3) part of the SU(3) gauge variable, in the maximal SO(3) gauge, as well as the positive SU(3) gauge action factor $e^{-S_G}$. Here, the SO(3) fermionic determinant is real, and it is non-negative for the even-number flavor case ($N_f=2n$) of the same quark mass, e.g., $m_u=m_d$. The SO(3) real algebra method alternates between the maximal SO(3) gauge fixing and Monte Carlo updates on the SO(3) determinant and $e^{-S_G}$. After the most importance sampling, the ratio of the SU(3) and SO(3) fermionic determinants is treated as a weight factor. If the phase factor of the ratio does not fluctuate significantly among the sampled gauge configurations for a set of parameters (e.g., volume, chemical potential, and quark mass), then SU(3) lattice QCD calculations at finite densities would be feasible.

2511.13551Nov 2025

View

QCD Equation of State at very high temperature: computational strategy, simulations and data analysis

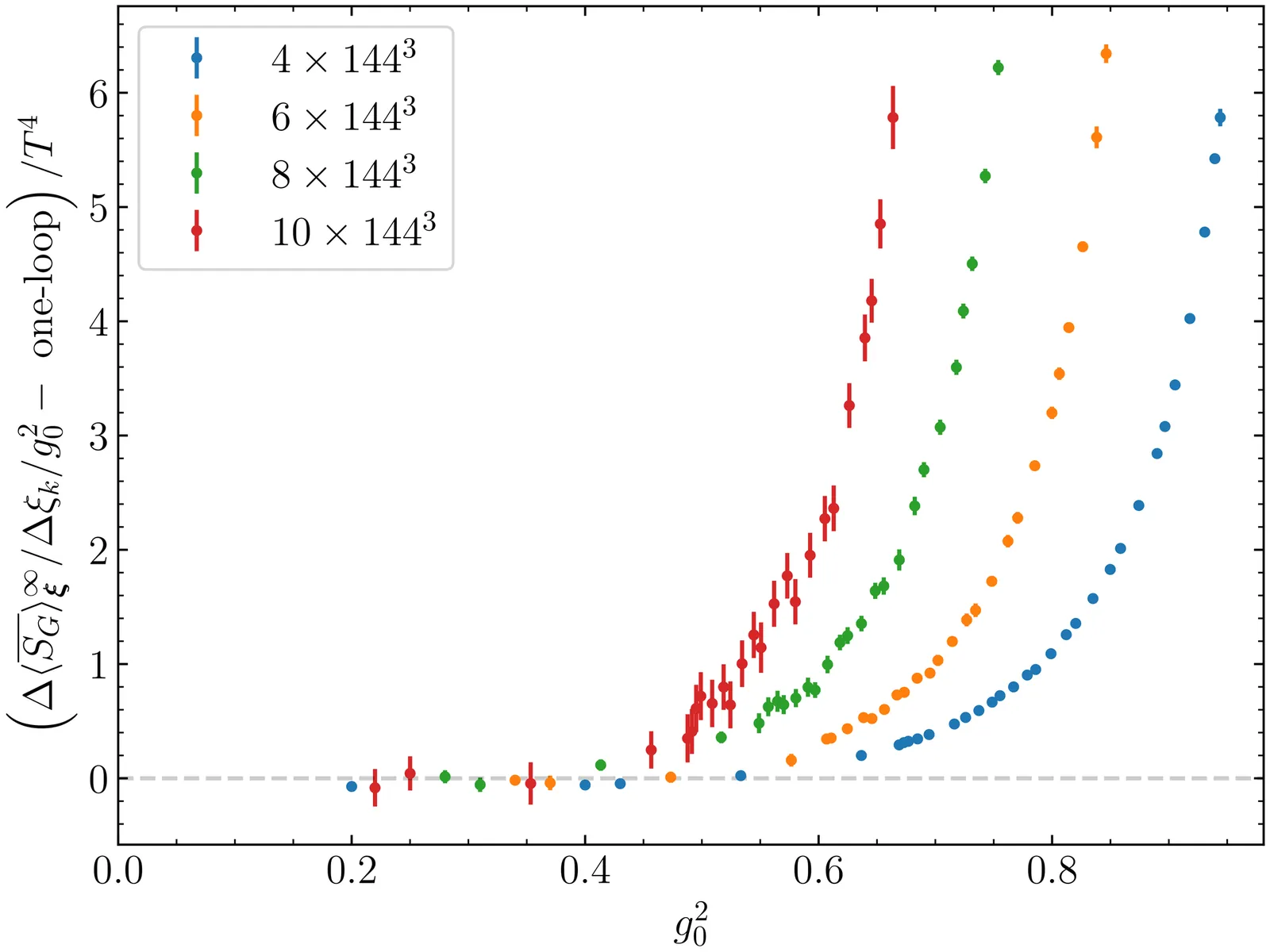
We present a detailed account of the theoretical progress and the computational strategy that led to the non-perturbative determination of the QCD Equation of State (EoS) at temperatures up to the electroweak scale reported in [Phys. Rev. Lett. 134, 201904 (2025)]. The two key ingredients that make such a calculation feasible with controlled uncertainties are: (i) the definition of lines of constant physics through the running of a non-perturbatively defined finite-volume coupling across a wide range of energy scales, and (ii) the use of shifted boundary conditions which allow a direct determination of the entropy density thus without the need for a zero-temperature subtraction. Considering the case of QCD with $N_f =3$ massless flavours in the temperature interval between 3 GeV and 165 GeV, we describe the numerical strategy based on integrating in the bare coupling and quark mass, the perturbative improvement of lattice observables, the optimization of numerical simulations, and the continuum extrapolation. Extensive consistency checks, including finite-volume and topological-freezing effects, confirm the robustness of the method. The final results have a relative accuracy of about $1\%$ or better, and the errors are dominated by the statistical fluctuations of the Monte Carlo ensembles. We also compare our non-perturbative results with predictions from standard and hard thermal loop perturbation theory showing that at the level of $\%$-precision contributions beyond those known, including non-perturbative ones due to ultrasoft modes, are relevant up to the highest temperatures explored. The methodological framework is general and readily applicable to QCD with four and five massive quark flavours and to other thermal observables, paving the way for systematic non-perturbative studies of thermal QCD at very high temperatures.

2511.09160Nov 2025

View

Page 1 of 37